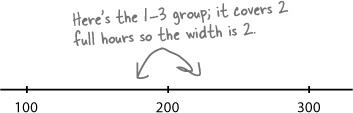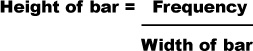Head First Statistics

Chapter 1. Visualizing Information: First Impressions

Can’t tell your facts from your figures?

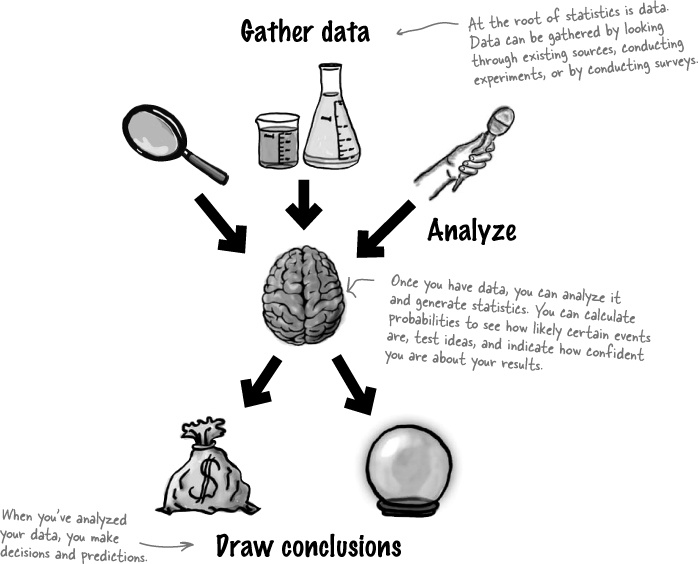
Statistics help you make sense of confusing sets of data. They make the complex simple. And when you’ve found out what’s really going on, you need a way of visualizing it and telling everyone else. So if you want to pick the best chart for the job, grab your coat, pack your best slide rule, and join us on a ride to Statsville.

Statistics are everywhere

Everywhere you look you can find statistics, whether you’re browsing the Internet, playing sports, or looking through the top scores of your favorite video game. But what actually is a statistic?

Statistics are numbers that summarize raw facts and figures in some meaningful way. They present key ideas that may not be immediately apparent by just looking at the raw data, and by data, we mean facts or figures from which we can draw conclusions. As an example, you don’t have to wade through lots of football scores when all you want to know is the league position of your favorite team. You need a statistic to quickly give you the information you need.

The study of statistics covers where statistics come from, how to calculate them, and how you can use them effectively.

But why learn statistics?

Understanding what’s really going on with statistics empowers you. If you really get statistics, you’ll be able to make objective decisions, make accurate predictions that seem inspired, and convey the message you want in the most effective way possible.

Statistics can be a convenient way of summarizing key truths about data, but there’s a dark side too.

Statistics are based on facts, but even so, they can sometimes be misleading. They can be used to tell the truth—or to lie. The problem is how do you know when you’re being told the truth, and when you’re being told lies?

Having a good understanding of statistics puts you in a strong position. You’re much better equipped to tell when statistics are inaccurate or misleading. In other words, studying statistics is a good way of making sure you don’t get fooled.

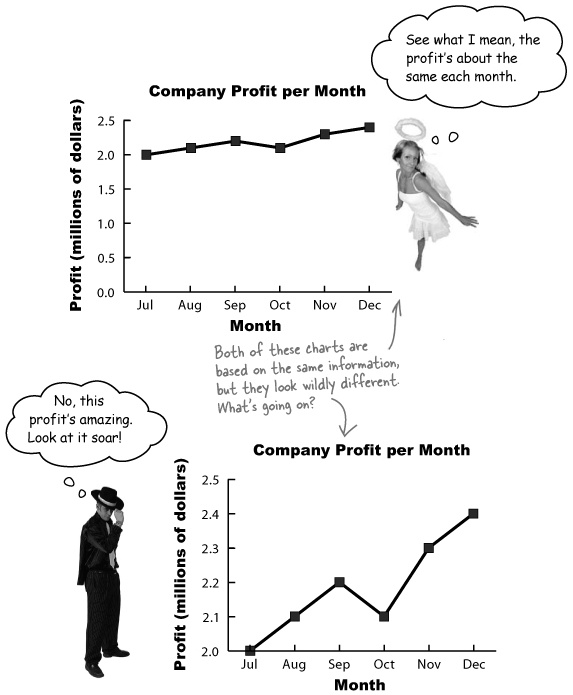
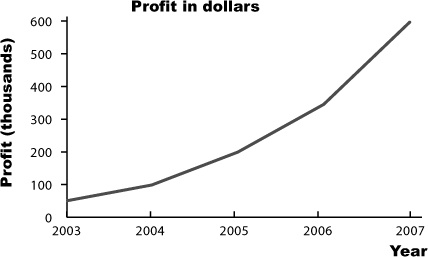
As an example, take a look at the profits made by a company in the latter half of last year.

Month	Jul	Aug	Sep	Oct	Nov	Dec
Profit (millions)	2.0	2.1	2.2	2.1	2.3	2.4

How can there be two interpretations of the same set of data? Let’s take a closer look.

A tale of two charts

So how can we explore these two different interpretations of the same data? What we need is some way of visualizing them. If you need to visualize information, there’s no better way than using a chart or graph. They can be a quick way of summarizing raw information and can help you get an impression of what’s going on at a glance. But you need to be careful because even the simplest chart can be used to subtly mislead and misdirect you.

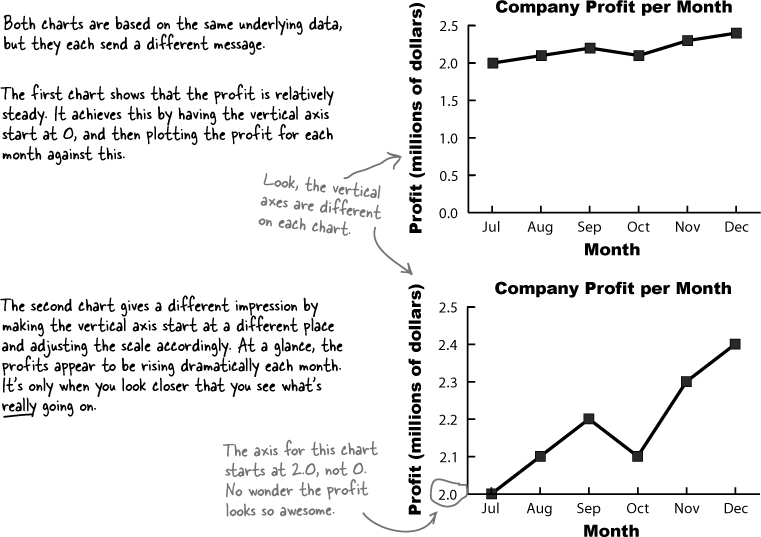
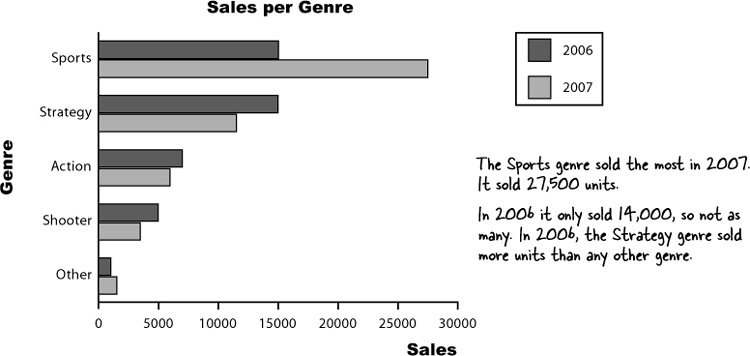
Here are two time graphs showing a companies profits for six months. They’re both based on the same information, so why do they look so different? They give drastically different versions of the same information.

Q:
Q: Why not just go on the data? Why chart it?
A:
A: Sometimes it’s difficult to see what’s really going on just by looking at the raw data. There can be patterns and trends in the data, but these can be very hard to spot if you’re just looking at a heap of numbers. Charts give you a way of literally seeing patterns in your data. They allow you to visualize your data and see what’s really going on in a quick glance.
Q:
Q: What’s the difference between information and data?
A:
A: Data refers to raw facts and figures that have been collected. Information is data that has some sort of added meaning.
As an example, take the numbers 5, 6, and 7. By themselves, these are just numbers. You don’t know what they mean or represent. They’re data. If you’re then told that these are the ages of three children, you have information as the numbers are now meaningful.

Software can’t think for you.

Chart software can save you a lot of time and produce effective charts, but you still need to understand what’s going on.

At the end of the day, it’s your data, and it’s up to you to choose the right chart for the job and make sure your data is presented in the most effective way possible and conveys the message you want.

Software can translate data into charts, but it’s up to you to make sure the chart is right.

Manic Mango needs some charts

One company that needs some charting expertise is Manic Mango, an innovative games company that is taking the world by storm. The CEO has been invited to deliver a keynote presentation at the next worldwide games expo. He needs some quick, slick ways of presenting data, and he’s asked you to come up with the goods. There’s a lot riding on this. If the keynote goes well, Manic Mango will get extra sponsorship revenue, and you’re bound to get a hefty bonus for your efforts.

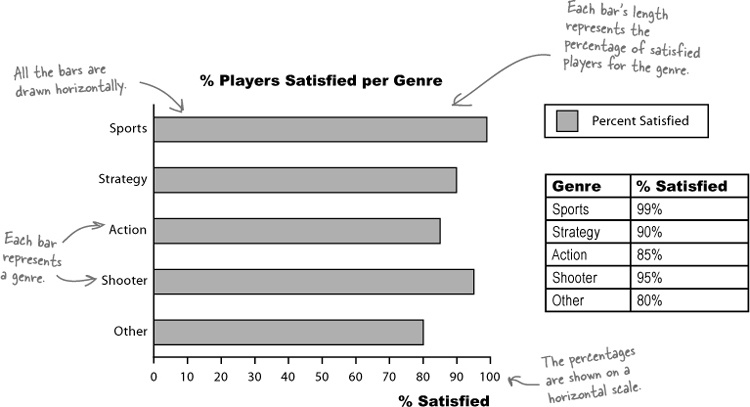
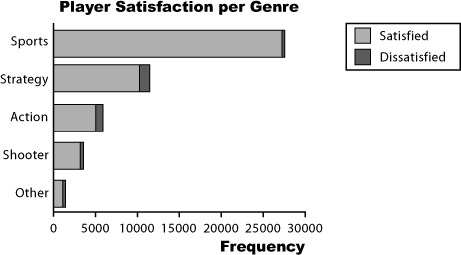
The first thing the CEO wants to be able to do is compare the percentage of satisfied players for each game genre. He’s started off by plugging the data he has through some charting software, and here are the results:

Brain Power

Take a good look at the pie chart that the CEO has produced. What does each slice represent? What can you infer about the relative popularity of different video game genres?

The humble pie chart

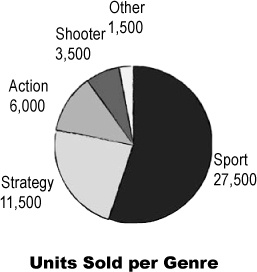
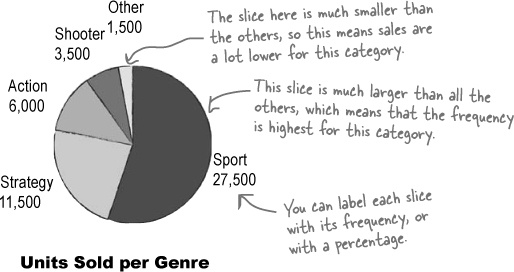
Pie charts work by splitting your data into distinct groups or categories. The chart consists of a circle split into wedge-shaped slices, and each slice represents a group. The size of each slice is proportional to how many are in each group compared with the others. The larger the slice, the greater the relative popularity of that group. The number in a particular group is called the frequency.

Pie charts divide your entire data set into distinct groups. This means that if you add together the frequency of each slice, you should get 100%.

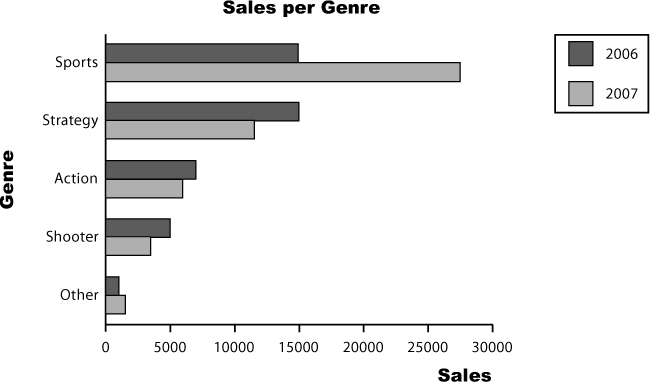
Let’s take a closer look at our pie chart showing the number of units sold per genre:

Genre	Units sold
Sports	27,500
Strategy	11,500
Action	6,000
Shooter	3,500
Other	1,500

So when are pie charts useful?

We’ve seen that the size of each slice represents the relative frequency of each group of data you’re showingg. Because of this, pie charts can be useful if you want to compare basic proportions. It’s usually easy to tell at a glance which groups have a high frequency compared with the others. Pie charts are less useful if all the slices have similar sizes, as it’s difficult to pick up on subtle differences between the slice sizes.

So what about the pie chart that the Manic Mango CEO has created?

Vital Statistics: Frequency

Frequency describes how many items there are in a particular group or interval. It’s like a count of how many there are.

Chart failure

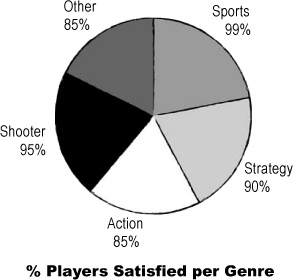
Creating a pie chart worked out so great for displaying the units sold per genre that the CEO’s decided to create another to chart consumer satisfaction with Manic Mango’s game. The CEO needs a chart that will allow him to compare the percentage of satisfied players for each game genre. He’s run the data through the charting software again, but this time he’s not as impressed.

Pie charts are used to compare the proportions of different groups or categories, but in this case there’s little variation between each group.

It’s difficult to take in at a glance which category has the highest level of player satisfaction.

It’s also generally confusing to label pie charts with percentages that don’t relate to the overall proportion of the slice. As an example, the Sports slice is labelled 99%, but it only fills about 20% of the chart. Another problem is that we don’t know whether there’s an equal number of responses for each genre, so we don’t know whether it’s fair to compare genre satisfaction in this way.

Pie charts show proportions

Brain Power

Take a look at the data, and think about the problems there are with this chart. What would be a better sort of chart for this kind of information?

Bar charts can allow for more accuracy

A better way of showing this kind of data is with a bar chart. Just like pie charts, bar charts allow you to compare relative sizes, but the advantage of using a bar chart is that they allow for a greater degree of precision. They’re ideal in situations where categories are roughly the same size, as you can tell with far greater precision which category has the highest frequency. It makes it easier for you to see small differences.

On a bar chart, each bar represents a particular category, and the length of the bar indicates the value. The longer the bar, the greater the value. All the bars have the same width, which makes it easier to compare them.

Bar charts can be drawn either vertically or horizontally.

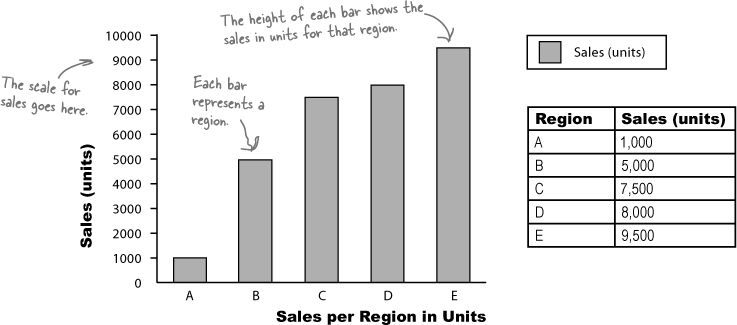
Vertical bar charts

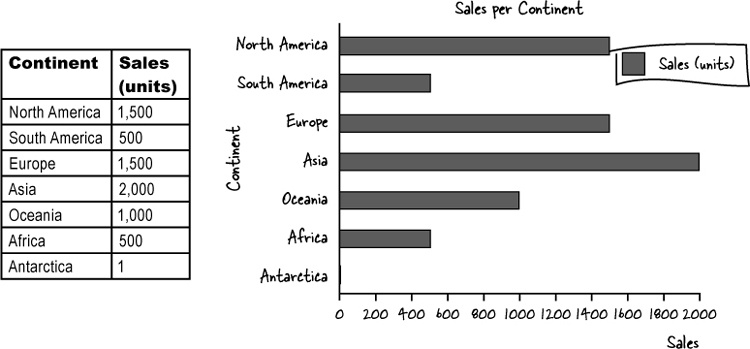
Vertical bar charts show categories on the horizontal axis, and either frequency or percentage on the vertical axis. The height of each bar indicates the value of its category. Here’s an example showing the sales figures in units for five regions, A, B, C, D, and E:

Horizontal bar charts

Horizontal bar charts are just like vertical bar charts except that the axes are flipped round. With horizontal bar charts, you show the categories on the vertical axis and the frequency or percentage on the horizontal axis.

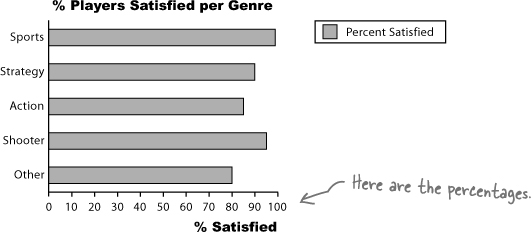
Here’s a horizontal bar chart for the CEO’s genre data from Chart failure. As you can see, it’s much easier to quickly gauge which category has the highest value, and which the lowest.

Vertical bar charts tend to be more common, but horizontal bar charts are useful if the names of your categories are long. They give you lots of space for showing the name of each category without having to turn the bar labels sideways.

It depends on what message you want to convey.

Let’s take a closer look.

It’s a matter of scale

Understanding scale allows you to create powerful bar charts that pick out the key facts you want to draw attention to. But be careful—scale can also conceal vital facts about your data. Let’s see how.

Using percentage scales

Let’s start by taking a deeper look at the bar chart showing player satisfaction per game genre. The horizontal axis shows player satisfaction as a percentage, the number of people out of every hundred who are satisfied with this genre.

The purpose of this chart is to allow us to compare different percentages and also read off percentages from the chart.

There’s just one problem—it doesn’t tell us how many players there are for each genre. This may not sound important, but it means that we have no idea whether this reflects the views of all players, some of them, or even just a handful. In other words, we don’t know how representative this is of players as a whole. The golden rule for designing charts that show percentages is to try and indicate the frequencies, either on the chart or just next to it.

Watch it!

Be very wary if you’re given percentages with no frequencies, or a frequency with no percentage.

Sometimes this is a tactic used to hide key facts about the underlying data, as just based on a chart, you have no way of telling how representative it is of the data. You may find that a large percentage of people prefer one particular game genre, but that only 10 people were questioned. Alternatively, you might find that 10,000 players like sports games most, but by itself, you can’t tell whether this is a high or low proportion of all game players.

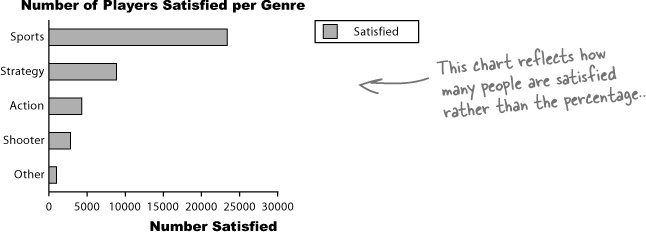
Using frequency scales

You can show frequencies on your scale instead of percentages. This makes it easy for people to see exactly what the frequencies are and compare values.

Normally your scale should start at 0, but watch out! Not every chart does this, and as you saw earlier in Sharpen your pencil Solution, using a scale that doesn’t start at 0 can give a different first impression of your data. This is something to watch out for on other people’s charts, as it’s very easy to miss and can give you the wrong impression of the data.

There are ways of drawing bar charts that give you more flexibility.

The problem with these bar charts is that they show either the number of satisfied players or the percentage, and they only show satisfied players.

Let’s take a look at how we can get around this problem.

Dealing with multiple sets of data

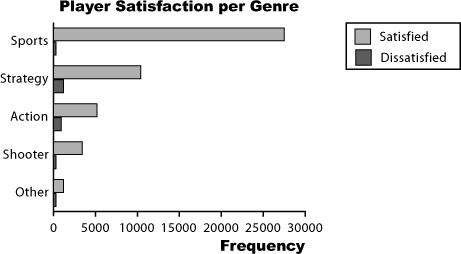
With bar charts, it’s actually really easy to show more than one set of data on the same chart. As an example, we can show both the percentage of satisfied players and the percentage of dissatisfied players on the same chart.

The split-category bar chart

One way of tackling this is to use one bar for the frequency of satisfied players and another for those dissatisfied, for each genre. This sort of chart is useful if you want to compare frequencies, but it’s difficult to see proportions and percentages.

The segmented bar chart

If you want to show frequencies and percentages, you can try using a segmented bar chart. For this, you use one bar for each category, but you split the bar proportionally. The overall length of the bar reflects the total frequency.

This sort of chart allows you to quickly see the total frequency of each category—in this case, the total number of players for each genre—and the frequency of player satisfaction. You can see proportions at a glance, too.

The CEO needs another chart for the keynote presentation. Here’s the data; see if you can sketch the bar chart.

Continent	Sales (units)
North America	1,500
South America	500
Europe	1,500
Asia	2,000
Oceania	1,000
Africa	500
Antarctica	1

Your bar charts rock

The CEO is thrilled with the bar charts you’ve produced, but there’s more data he needs to present at the keynote.

Brain Power

Look back through the chapter. How do you think this type of data is different? What impact do you think this could have on charts?

Categories vs. numbers

When you’re working with charts, one of the key things you need to figure out is what sort of data you’re dealing with. Once you’ve figured that out, you’ll find it easier to make key decisions about what chart you need to best represent your data.

Categorical or qualitative data

Most of the data we’ve seen so far is categorical. The data is split into categories that describe qualities or characteristics. For this reason, it’s also called qualitative data. An example of qualitative data is game genre; each genre forms a separate category.

The key thing to remember with qualitative data is that the data values can’t be interpreted as numbers.

breed of dog

type of dessert

Numerical or quantitative data

Numerical data, on the other hand, deals with numbers. It’s data where the values have meaning as numbers, and that involves measurements or counts. Numerical data is also called quantitative data because it describes quantities.

weight

length

time

So what impact does this have on the chart for Manic Mango?

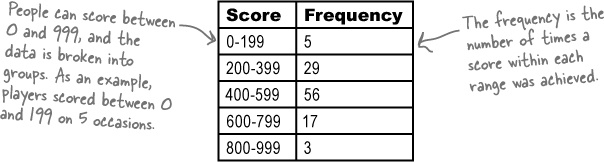
Dealing with grouped data

The latest set of data from the Manic Mango CEO is numeric and, what’s more, the scores are grouped into intervals. So what’s the best way of charting data like this?

Note

The scores are numeric and grouped into intervals

Score	Frequency
0-199	5
200-399	29
400-599	56
600-799	17
800-999	3

We could, but there’s a better way.

Rather than treat each range of scores as a separate category, we can take advantage of the data being numeric, and present the data using a continuous numeric scale instead. This means that instead of using bars to represent a single item, we can use each bar to represent a range of scores.

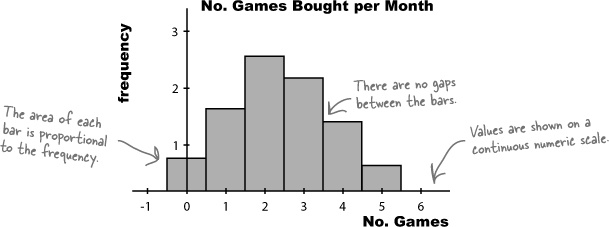
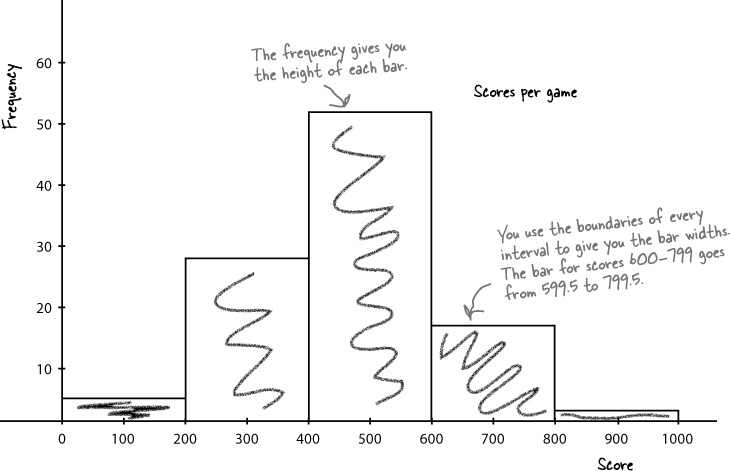
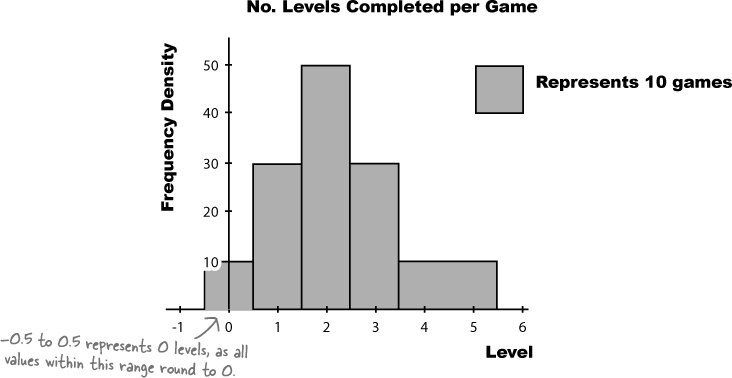
To do this, we can create a histogram.

Histograms are like bar charts but with two key differences. The first is that the area of each bar is proportional to the frequency, and the second is that there are no gaps between the bars on the chart. Here’s an example of a histogram showing the average number of games bought per month by households in Statsville:

To make a histogram, start by finding bar widths

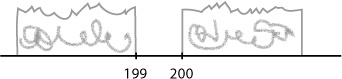
The first step to creating a histogram is to look at each of the intervals and work out how wide each of them needs to be, and what range of values each one needs to cover. While doing this, we need to make sure that there will be no gaps between the bars on the histogram.

Let’s start with the first two intervals, 0–199 and 200–399. At face value, the first interval finishes at score 199, and the second starts at score 200. The problem with plotting it like this, however, is that it would leave a gap between score 199 and 200, like this:

Score	Frequency
0–199	5
200–399	29
400–599	56
600–799	17
800–999	3

Histograms shouldn’t have gaps between the bars, so to get around this, we extend their ranges slightly. Instead of one interval ending at score 199 and the next starting at score 200, we make the two intervals meet at 199.5, like this:

Doing this forms a single boundary and makes sure that there are no gaps between the bars on the histogram. If we complete this for the rest of the intervals, we get the following boundaries:

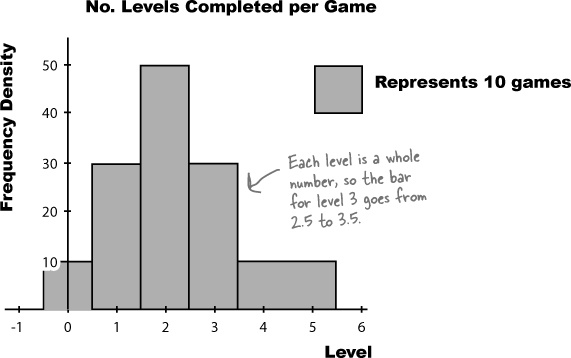
Each interval covers 200 scores, and the width of each interval is 200. Each interval has the same width.

As all the intervals have the same width, we create the histogram by drawing vertical bars for each range of scores, using the boundaries to form the start and end point of each bar. The height of each bar is equal to the frequency.

Here’s a reminder of the data for Manic Mango.

Score	Frequency
0–199	5
200–399	29
400–599	56
600–799	17
800–999	3

See if you can use the class boundaries to create a histogram for this data. Remember, the frequency goes on the vertical axis.

Here’s a reminder of the data for Manic Mango.

Score	Frequency
0–199	5
200–399	29
400–599	56
600–799	17
800–999	3

See if you can use the class boundaries to create a histogram for this data. Remember, the frequency goes on the vertical axis.

Q:
Q: So is a histogram basically for grouped numeric data?
A:
A: Yes it is. The advantage of a histogram is that because its numeric, you can use it to show the width of each interval as well as the frequency.
Q:
Q: What about if the intervals are different widths? Can you still use a histogram?
A:
A: Absolutely. It’s more common for the interval widths to be equal size, but with a histogram they don’t have to be. There are a couple more steps you need to go through to create a histogram with unequal sized intervals, but we’ll show you that very soon.
Q:
Q: Why shouldn’t histograms have gaps between the bars?
A:
A: There are at least two good reasons. The first is to show that there are no gaps in the values, and that every value is covered. The second is so that the width of the interval reflects the range of the values you’re covering. As an example, if we drew the interval 0–199 as extending from value 0 to value 199, the width on the chart would only be 199 – 0 = 199.
Q:
Q: So why do we make the bars meet midway between the two?
A:
A: The bars have to meet, and it’s usually at the midway point, but it all comes down to how you round your values. When you round values, you normally round them to the nearest whole number. This means that the range of values from -0.5 to 0.5 all round to 0, and so when we show 0 on a histogram, we show it using the range of values from -0.5 to 0.5.
Q:
Q: Are there any exceptions to this?
A:
A: Yes, age is one exception. If you have to represent the age range 18–19 on a histogram, you would normally represent this using an interval that goes from 18 to 20. The reason for this is that we typically classify someone as being 19, for example, up until their 20th birthday. In effect, we round ages down.

The frequency is a statistical way of saying how many items there are in a category.
Pie charts are good for showing basic proportions.
Bar charts give you more flexibility and precision.
Numerical data deals with numbers and quantities; categorical data deals with words and qualities.
Horizontal bar charts are used for categorical data, particularly where the category names are long.
Vertical bar charts are used for numerical data, or categorical data if the category names are short.
You can show multiple sets of data on a bar chart, and you have a choice of how to do this. You can compare frequencies by showing related bars side-by-side on a split-category bar chart. You can show proportions and total frequencies by stacking the bars on top of each other on a segmented bar chart.
Bar chart scales can show either percentages or frequencies.
Each chart comes in a number of different varieties.

Manic Mango needs another chart

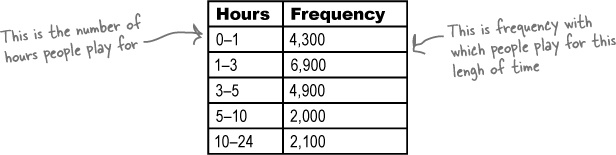
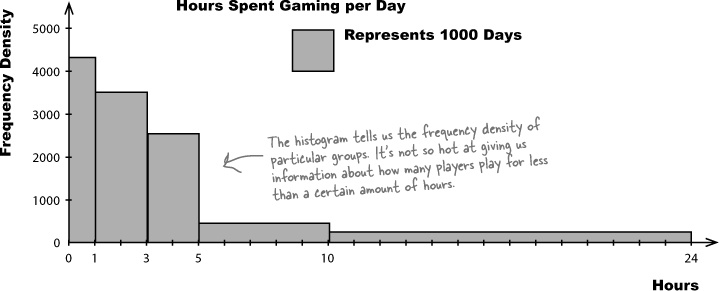
The CEO is very pleased with the histogram you’ve created for him—so much so, that he wants you to create another histogram for him. This time, he wants a chart showing for how long Manic Mango players tend to play online games over a 24-hour period. Here’s the data:

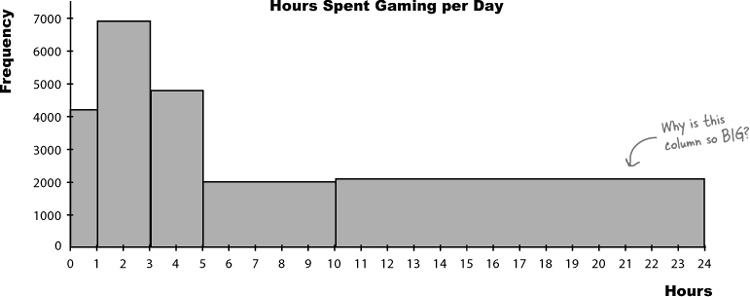
He’s right, the interval widths aren’t all equal.

If you take a look at the intervals, you can see that they’re different widths. As an example, the 10–24 range covers far more hours than the 0–1 range.

If we had access to the raw data, we could look at how we could construct equal width intervals, but unfortunately this is all the data we have. We need a way of drawing a histogram that makes allowances for the data having different widths.

Brain Power

For histograms, the frequency is proportional to the area of each bar. How would you use this to create a histogram for this data? What do you need to be aware of?

Do you think she’s right?

Here’s a sketch of the chart, using frequency on the vertical scale and drawing bar widths proportional to their interval size. Do you see any problems?

A histogram’s bar area must be proportional to frequency

The problem with this chart is that making the width of each bar reflect the width of each interval has made some of the bars look disproportionately large. Just glancing at the chart, you might be left with a misleading impression about how many hours per day people really play games for. As an example, the bar that takes up the largest area is the bar showing game play of 10–24 hours, even though most people don’t play for this long.

As this is a histogram, we need to make the bar area proportional to the frequency it represents. As the bars have unequal widths, what should we do to the bar height?

Make the area of histogram bars proportional to frequency

Up until now, we’ve been able to use the height of each bar to represent the frequency of a particular number or category.

This time around, we’re dealing with grouped numeric data where the interval widths are unequal. We can make the width of each bar reflect the width of each interval, but the trouble is that having bars of different widths affects the overall area of each bar.

We need to make sure the area of each bar is proportional to its frequency. This means that if we adjust bar width, we also need to adjust bar height. That way, we can change the widths of the bars so that they reflect the width of the group, but we keep the size of each bar in line with its frequency.

Let’s go through how to create this new histogram.

For histograms, the frequency is represented by bar area

Step 1: Find the bar widths

We find how wide our bars need to be by looking at the range of values they cover. In other words, we need to figure out how many full hours are covered by each group.

Let’s take the 1–3 group. This group covers 2 full hours, 1–2 and 2–3. This means that the width of the bar needs to be 2, with boundaries of 1 and 3.

If we calculate the rest of the widths, we get:

Hours	Frequency	Width
0–1	4,300	1
1–3	6,900	2
3–5	4,900	2
5–10	2,000	5
10–24	2,100	14

Now that we’ve figured out the bar widths, we can move onto working out the heights.

Step 2: Find the bar heights

Now that we have the widths of all the groups, we can use these to find the heights the bars need to be. Remember, we need to adjust the bar heights so that the overall area of each bar is proportional to the group’s frequency.

First of all, let’s take the area of each bar. We’ve said that frequency and area are equivalent. As we already know what the frequency of each group is, we know what the areas should be too:

Area of bar = Frequency of group

Note

We were given these right at the start, so we know what area we’re aiming for.

Now each bar is basically just a rectangle, which means that the area of each bar is equal to the width multiplied by the height. As the area gives us the frequency, this means:

Frequency = Width of bar × Height of bar

We found the widths of the bars in the last step, which means that we can use these to find what height each bar should be. In other words,

The height of the bar is used to measure how concentrated the frequency is for a particular group. It’s a way of measuring how densely packed the frequency is, a way of saying how thick or thin on the ground the numbers are. The height of the bar is called the frequency density.

What should the height of each bar be? Complete the table.

Hours	Frequency	Width	Height (Frequency Density)
0–1	4,300	1	4,300 ÷ 1 = 4,300
1–3	6,900	2
3–5	4,900	2
5–10	2,000	5
10–24	2,100	14

What should the height of each bar be? Complete the table.

Hours	Frequency	Width	Height (Frequency Density)
0–1	4,300	1	4,300 ÷ 1 = 4,300
1–3	6,900	2	6,900 ÷ 2 = 3,450
3–5	4,900	2	4,900 ÷ 2 = 2,450
5–10	2,000	5	2,000 ÷ 5 = 400
10–24	2100	14	2,100 ÷ 14 = 150

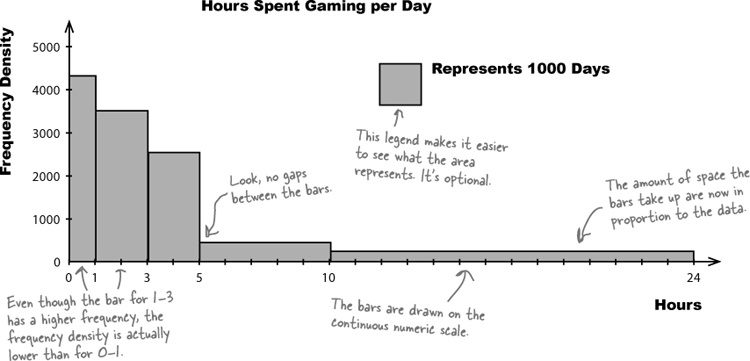
Step 3: Draw your chart—a histogram

Now that we’ve worked out the widths and heights of each bar, we can draw the histogram. We draw it just like before, except that this time, we use frequency density for the vertical axis and not frequency.

Here’s our revised histogram.

Frequency density refers to the concentration of values in data. It’s related to frequency, but it’s not the same thing. Here’s an analogy to demonstrate the relationship between the two.

Imagine you have a quantity of juice that you’ve poured into a glass like this:

What if you then pour the same quantity of juice into a different sized glass, say one that’s wider? What happens to the level of the juice? This time the glass is wider, so the level the juice comes up to is lower.

The level of the juice varies in line with the width of the glass; the wider the glass, the lower the level. The converse is true too; the narrower the glass, the higher the level of juice.

So what does juice have to do with frequency density?

Juice = Frequency

Imagine that instead of pouring juice into glasses, you’re “pouring” frequency into the bars on your chart. Just as you know the width of the glass, you know what width your bars are. And just like the space the juice occupies in the glass (width x height) tells you the quantity of juice in the glass, the area of the bar on the graph is equivalent to its frequency.

The frequency density is then equal to the height of the bar. Keeping with our analogy, it’s equivalent to the level your juice comes to in each glass. Just as a wider glass means the juice comes to a lower level, a wider bar means a lower frequency density.

Frequency density relates to how concentrated the frequencies are for grouped data. It’s calculated using
A histogram is a chart that specializes in grouped data. It looks like a bar chart, but the height of each bar equates to frequency density rather than frequency.
When drawing histograms, the width of each bar is proportional to the width of its group. The bars are shown on a continuous numeric scale.
In a histogram, the frequency of a group is given by the area of its bar.
A histogram has no gaps between its bars.

Q:
Q: Why do we use area to represent frequency when we’re graphing histograms?
A:
A: It’s a way of making sure the relative sizes of each group stay in proportion to the data, and stay honest. With grouped data, we need a visual way of expressing the width of each group and also its frequency. Changing the width of the bars is an intuitive way of reflecting the group range, but it has the side effect of making some of the bar sizes look disproportionate.
Adjusting the bar height and using the area to represent frequency is a way around this. This way, no group is misrepresented by taking up too much or too little space.
Q:
Q: What’s frequency density again?
A:
A: Frequency density is a way of indicating how concentrated values are in a particular interval. It gives you a way of comparing different intervals that may be different widths. It makes the frequency proportional to the area of a bar, rather than height.
To find the frequency density, take the frequency of an interval, and divide it by the width.
Q:
Q: If I have grouped numeric data, but all the intervals are the same width, can I use a normal bar chart?
A:
A: Using a histogram will better represent your data, as you’re still dealing with grouped data. You really want your frequency to be proportional to its area, not height.
Q:
Q: Do histograms have to show grouped data? Can you use them for individual numbers as well as groups of numbers?
A:
A: Yes, you can. The key thing to remember is to make sure there are no gaps between the bars and that you make each bar 1 wide. Normally you do this by positioning your number in the center of the bar.
As an example, if you wanted to draw a bar representing the individual number 1, then you’d draw a bar ranging from 0.5 to 1.5, with 1 in the center.

Here’s a histogram representing the number of levels completed in each game of Cows Gone Wild. How many games have been played in total? Assume each level is a whole number.

We need to find the total number of games played, which means we need to find the total frequency.

The total frequency is equal to the area of each bar added together. In other words, we multiply the width of each bar by its frequency density to get the frequency, and then add the whole lot up together.

Level	Width	Frequency Density	Frequency
0	1	10	1x10 = 10
1	1	30	1x30 = 30
2	1	50	1x50 = 50
3	1	30	1x30 = 30
4–5	2	10	2x10 = 20

Total Frequency	= 10 + 30 + 50 + 30 + 20
	= 140

Histograms can’t do everything

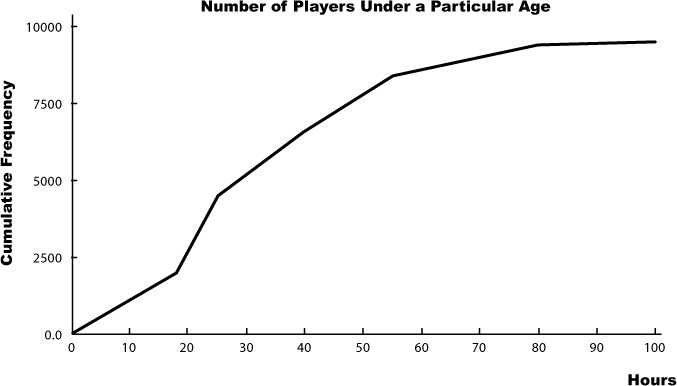
While histograms are an excellent way to display grouped numeric data, there are still some kinds of this data they’re not ideally suited for presenting—like running totals...

Let’s see if we can help the CEO out. Here’s the histogram we had before.

It’s tricky to see at a glance what the running totals are in this chart. In order to find the frequency of players playing for up to 5 hours, we need to add different frequencies together. We need another sort of chart...but what?

Brain Power

What sort of information do you think we should show on the chart? What sort of information should we plot? Write your answer below.

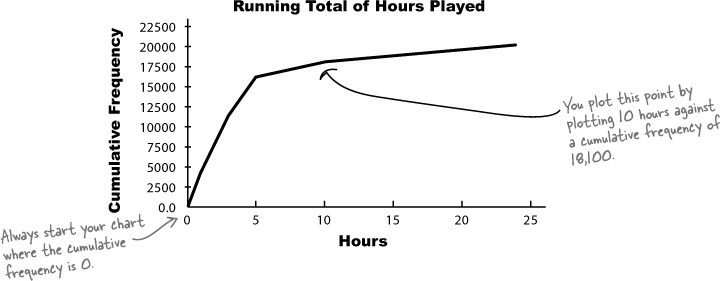
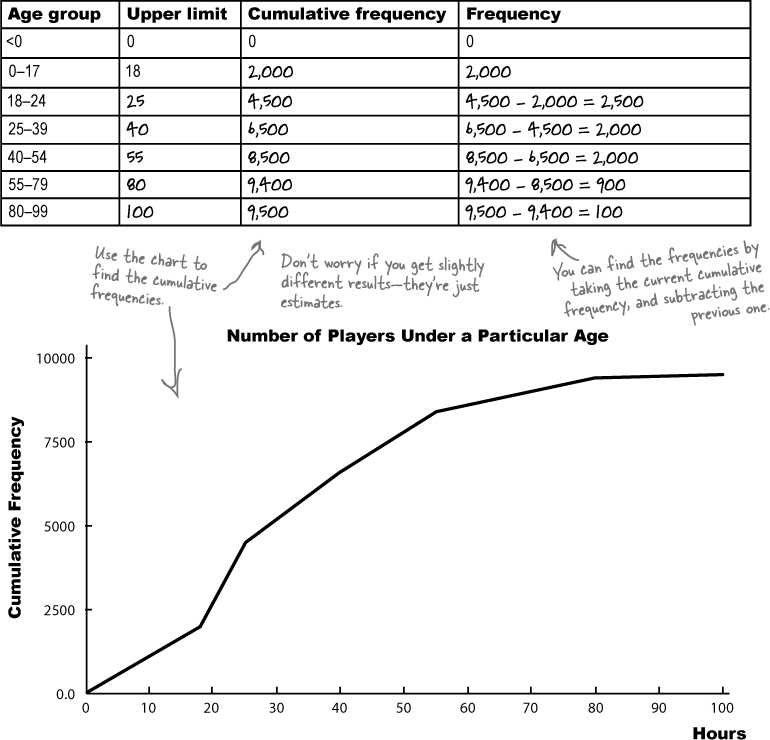
Introducing cumulative frequency

The CEO needs some sort of chart that will show him the total frequency below a particular value: the cumulative frequency. By cumulative frequency, we basically mean a running total.

What we need to come up with is some sort of graph that shows hours on the horizontal axis and cumulative frequency on the vertical axis. That way, the CEO will be able to take a value and read off the corresponding frequency up to that point. He’ll be able to find out how many people play for up to 5 hours, 6 hours, or whatever other number of hours he’s most interested in at the time.

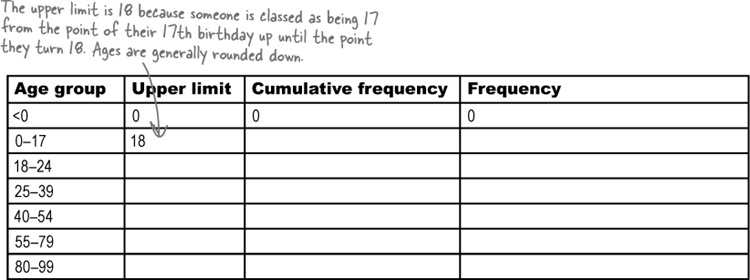
Before we can draw the chart, we need to know what exactly we need to plot on the chart. We need to calculate cumulative frequencies for each of the intervals that we have, and also work out the upper limit of each interval.

Let’s start by looking at the data.

Vital Statistics: Cumulative Frequency

The total frequency up to certain value. It’s basically a running total of the frequencies.

Hours	Frequency
0–1	4,300
1–3	6,900
3–5	4,900
5–10	2,000
10–24	2,100

Note

Here’s the data.

So what are the cumulative frequencies?

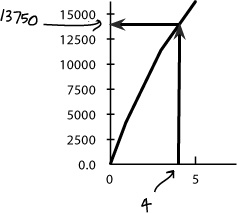
First off, let’s suppose the CEO needs to plot the cumulative frequency, or total frequency, of up to 1 hour. If we look at the data, we know that the frequency of the 0–1 group is 4300, and we can see that is the upper limit of the group. This means that the cumulative frequency of hours up to 1 is 4300.

Next, let’s look at the total frequency up to 3. We know what the frequencies are for the 0–1 and 1–3 groups, and 3 is again the upper limit. To find the total frequency of hours up to 3, we add together the frequency of the 0–1 group and the 1–3 group.

Can you see a pattern? If we take the upper limit of each of the groups of hours, we can find the total frequency of hours up to that value by adding together the frequencies. Applying this to all the groups gives us

Hours	Frequency	Upper limit	Cumulative frequency
0	0	0	0
0–1	4,300	1	4,300
1–3	6,900	3	4,300+6,900 = 11,200
3–5	4,900	5	4,300+6,900+4,900 = 16,100
5–10	2,000	10	4,300+6,900+4,900+2,000 = 18,100
10–24	2,100	24	4,300+6,900+4,900+2,000+2,100 = 20,200

Note

We’ve added in 0, as you can’t play games for LESS than 0 hours a week.

Drawing the cumulative frequency graph

Now that we have the upper limits and cumulative frequencies, we can plot them on a chart. Draw two axes, with the vertical one for the cumulative frequency and the horizontal one for the hours. Once you’ve done that, plot each of the upper limits against its cumulative frequency, and then join the points together with a line like this:

Watch it!

Cumulative frequencies can never decrease.

If your cumulative frequency decreases at any point, check your calculations.

The CEO wants you to find the number of instances of people playing online for less than 4 hours. See if you can estimate this using the cumulative frequency diagram.

To do this, we find 4 on the horizontal axis, find where this value meets the line of the graph, and read off the corresponding cumulative frequency on the vertical axis.

This gives us an answer of approximately 13,750. In other words, there are approximately 13,750 instances of people playing online for under 4 hours.

Q:
Q: What’s a cumulative frequency?
A:
A: The cumulative frequency of a value is the sum of the frequencies up to and including that value. It tells you the total frequency up to that point.
As an example, suppose you have data telling you how old people are. The cumulative frequency for value 27 tells you how many people there are up to and including age 27.
Q:
Q: Are cumulative frequency graphs just for grouped data?
A:
A: Not at all; you can use them for any sort of numeric data. The key thing is whether you want to know the total frequency up to a particular value, or whether you’re more interested in the frequencies of particular values instead.
Q:
Q: On some charts you can show more than one set of data on the same chart. What about for cumulative frequency graphs?
A:
A: You can do this for cumulative frequency graphs by drawing a separate line for each set of data. If, say, you wanted to compare the cumulative frequencies by gender, you could draw one line showing males and the other females. It would be far more effective to show both lines on one chart, as it makes it easier to compare the two sets of data.
Q:
Q: Is there a limit to how many lines you can show on one chart?
A:
A: There’s no specific limit, as it all depends on your data. Don’t have so many lines that the graph becomes cluttered and you can no longer use it to read off cumulative frequencies and compare sets of data.
Q:
Q: Remind me, how do I find the cumulative frequency of a value?
A:
A: You can find the cumulative frequency by reading it straight off the graph. You locate the value you want to find the cumulative frequency for on the horizontal axis, find where this meets the cumulative frequency curve, and then read the value of cumulative frequency off the vertical axis.
Q:
Q: If I already know the cumulative frequency, can I use the graph to find the corresponding value?
A:
A: Yes you can. Look for the cumulative frequency on the vertical axis, find where it meets the cumulative frequency curve, and then read off the value.

Choosing the right chart

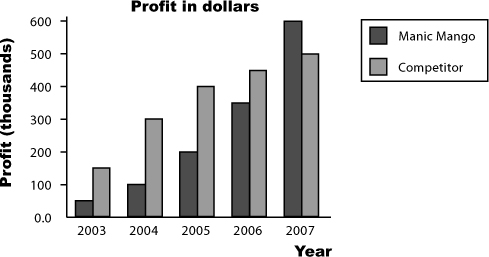
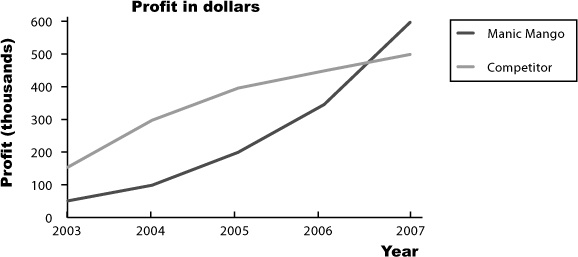
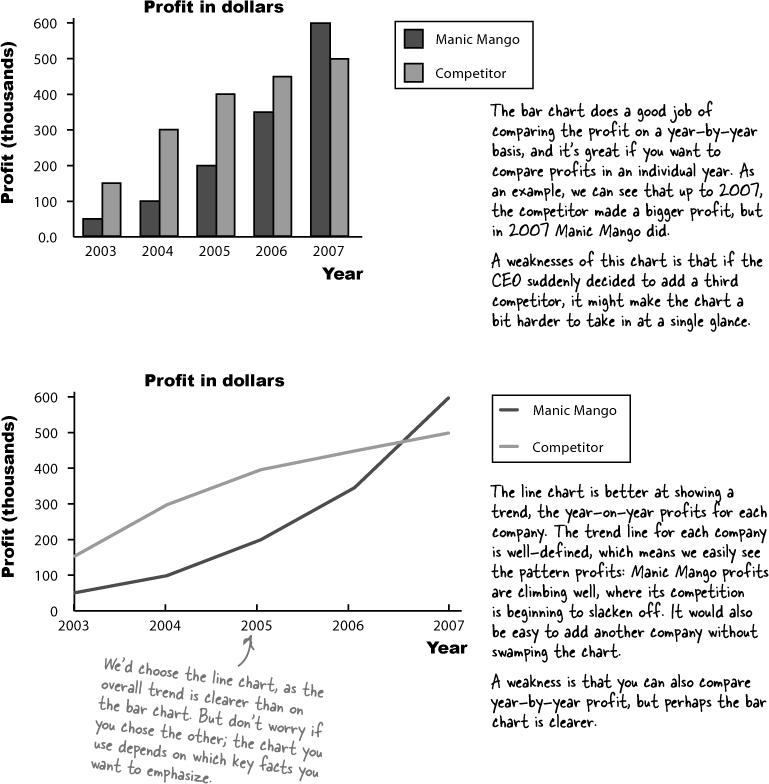
The CEO is really happy with your work on cumulative frequency graphs, and your bonus is nearly in the bag. He’s nearly finished preparing for the keynote, but there’s just one more thing he needs: a chart showing Manic Mango profits compared with the profits of their main rivals. Which chart should he use?

Line charts are good at showing trends in your data. For each set of data, you plot your points and then join them together with lines. You can easily show multiple sets of data on the same chart without it getting too cluttered. Just make sure it’s clear which line is which.

As with other sorts of charts, you have a choice of showing frequency or percentages on the vertical axis. The scale you use all depends on what key facts you want to draw out.

Line charts are often used to show time measurements. Time always goes on the horizontal axis, and frequency on the vertical. You can read off the frequency for any period of time by choosing the time value on the horizontal axis, and reading off the corresponding frequency for that point on the line.

Line charts should be used for numerical data only, and not categorical. This is because it makes sense to compare different categories, but not to draw a trend line. Only use a line chart if you’re comparing categories over some numerical unit such as time, and in that case you’d use a separate line for each category.

Cumulative frequency is the total frequency up to a particular value. It’s a running total of the frequencies.
Use a cumulative frequency graph to plot the upper limit of each group of data against cumulative frequency.
Use a line chart if you want to show trends, for example over time.
You can show more than one set of data on a line chart. Use one line for each set of data, and make sure it’s clear which line is which.
You can use line charts to make basic predictions as it’s easy to see the shape of the trend. Just extend the trend line, trying to keep the same basic shape.
Don’t use line charts to show categorical data unless you’re showing trends for each category, for example over time. If you do this, draw one line per category.

Q:
Q: Are line charts the same thing as time series charts? I think I’ve heard that name used before.
A:
A: A time series chart is really a line chart that focuses on time intervals, just like the examples we used. A line chart doesn’t have to focus on just time, though.
Q:
Q: Are there any special varieties of line charts?
A:
A: Yes. In fact, you’ve encountered one of them already. The cumulative frequency graph is a type of line chart that shows the total frequency up to a certain value.
Q:
Q: Can line charts show categorical data as well as data that’s numeric?
A:
A: Line charts should only be used to show categorical data if you’re showing trends for each category, and use a separate line for each category.
What you shouldn’t do is use a line chart to draw lines from category to category.
Q:
Q: So line charts are better for showing overarching trends, and bar charts are better for comparing values or categories?
A:
A: That’s right. Which chart you use really comes down to what message you want to put across, and what key facts you want to minimize.
Q:
Q: Now that I know how to create charts properly, can I use charting software to do the heavy lifting?
A:
A: Absolutely! Charting software can save you a lot of time and hard work, and the results can be excellent.
The key thing with using software to produce your charts is to remember that the software can’t think for you. You still have to decide which chart best represents your key facts, and you have to check that the software produces exactly what you expect it to.

Manic Mango conquered the games market!

You’ve helped produce some killer charts for Manic Mango, and thanks to you, the keynote was a huge success. Manic Mango has gained tons of extra publicity for their games, and money from sponsorship and advertising is rolling in. The only thing left for you to do is think about all the things you could do and the places you could go with your well-earned bonus.

You’ve had your first taste of how statistics can help you and what you can achieve by understanding what’s really going on. Keep reading and we’ll show you more things you can do with statistics, and really start to flex those statistics muscles.

Get Head First Statistics now with the O’Reilly learning platform.

O’Reilly members experience books, live events, courses curated by job role, and more from O’Reilly and nearly 200 top publishers.

Start your free trial

Chapter 1. Visualizing Information: First Impressions

Statistics are everywhere

But why learn statistics?

A tale of two charts

Manic Mango needs some charts

Brain Power

The humble pie chart

So when are pie charts useful?

Vital Statistics: Frequency

Chart failure

Brain Power

Bar charts can allow for more accuracy

Vertical bar charts

Horizontal bar charts

It’s a matter of scale

Using percentage scales

Watch it!

Using frequency scales

Dealing with multiple sets of data

The split-category bar chart

The segmented bar chart

Your bar charts rock

Brain Power

Categories vs. numbers

Categorical or qualitative data

Numerical or quantitative data

Dealing with grouped data

Note

To make a histogram, start by finding bar widths

Manic Mango needs another chart

Brain Power

A histogram’s bar area must be proportional to frequency

Make the area of histogram bars proportional to frequency

Step 1: Find the bar widths

Step 2: Find the bar heights

Note

Step 3: Draw your chart—a histogram

Histograms can’t do everything

Brain Power

Introducing cumulative frequency

Vital Statistics: Cumulative Frequency

Note

So what are the cumulative frequencies?

Note

Drawing the cumulative frequency graph

Watch it!

Choosing the right chart

Manic Mango conquered the games market!

Don’t leave empty-handed

It’s yours, free.

Check it out now on O’Reilly