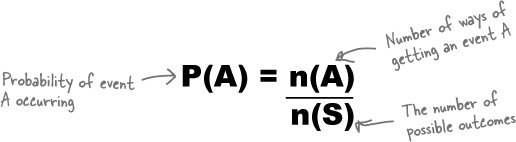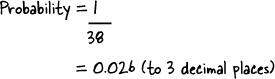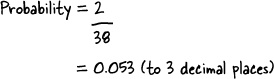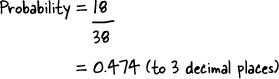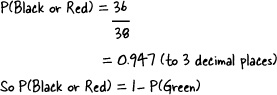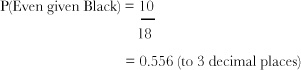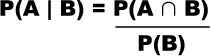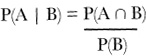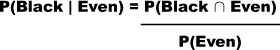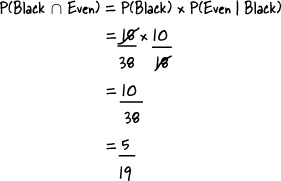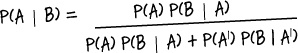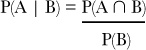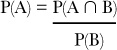Chapter 4. Calculating Probabilities: Taking Chances
Sometimes it can be impossible to say what will happen from one minute to the next. But certain events are more likely to occur than others, and that’s where probability theory comes into play. Probability lets you predict the future by assessing how likely outcomes are, and knowing what could happen helps you make informed decisions. In this chapter, you’ll find out more about probability and learn how to take control of the future!
Fat Dan’s Grand Slam
Fat Dan’s Casino is the most popular casino in the district. All sorts of games are offered, from roulette to slot machines, poker to blackjack.
It just so happens that today is your lucky day. Head First Labs has given you a whole rack of chips to squander at Fat Dan’s, and you get to keep any winnings. Want to give it a try? Go on—you know you want to.
There’s a lot of activity over at the roulette wheel, and another game is just about to start. Let’s see how lucky you are.
Roll up for roulette!
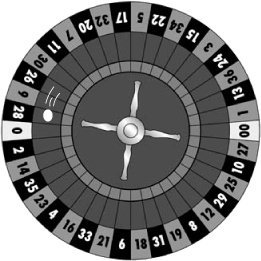
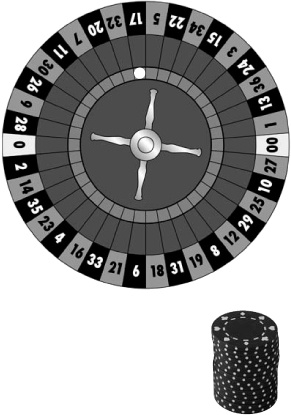
You’ve probably seen people playing roulette in movies even if you’ve never tried playing yourself. The croupier spins a roulette wheel, then spins a ball in the opposite direction, and you place bets on where you think the ball will land.
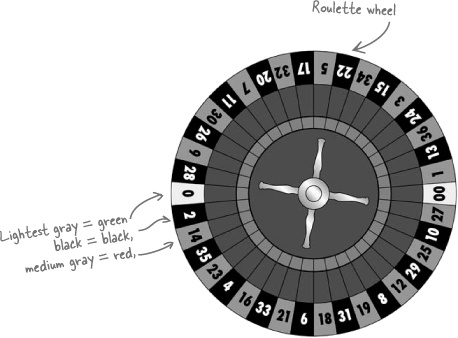
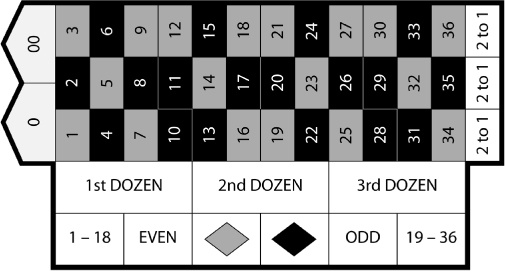
The roulette wheel used in Fat Dan’s Casino has 38 pockets that the ball can fall into. The main pockets are numbered from 1 to 36, and each pocket is colored either red or black. There are two extra pockets numbered 0 and 00. These pockets are both green.
You can place all sorts of bets with roulette. For instance, you can bet on a particular number, whether that number is odd or even, or the color of the pocket. You’ll hear more about other bets when you start playing. One other thing to remember: if the ball lands on a green pocket, you lose.
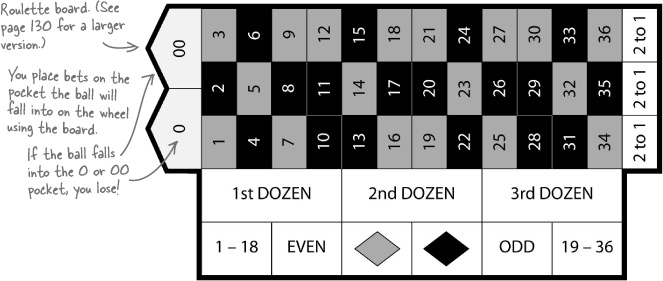
Roulette boards make it easier to keep track of which numbers and colors go together.
Your very own roulette board
You’ll be placing a lot of roulette bets in this chapter. Here’s a handy roulette board for you to cut out and keep. You can use it to help work out the probabilities in this chapter.
Place your bets now!
Have you cut out your roulette board? The game is just beginning. Where do you think the ball will land? Choose a number on your roulette board, and then we’ll place a bet.
Right, before placing any bets, it makes sense to see how likely it is that you’ll win.
Maybe some bets are more likely than others. It sounds like we need to look at some probabilities...
What are the chances?
Have you ever been in a situation where you’ve wondered “Now, what were the chances of that happening?” Perhaps a friend has phoned you at the exact moment you’ve been thinking about them, or maybe you’ve won some sort of raffle or lottery.
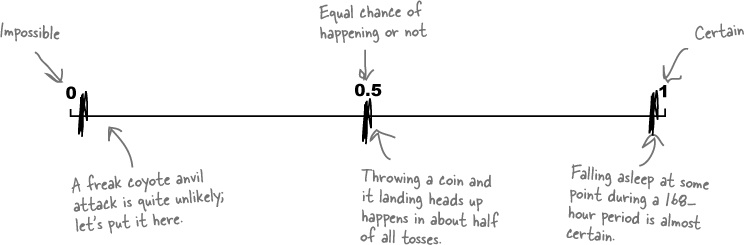
Probability is a way of measuring the chance of something happening. You can use it to indicate how likely an occurrence is (the probability that you’ll go to sleep some time this week), or how unlikely (the probability that a coyote will try to hit you with an anvil while you’re walking through the desert). In stats-speak, an event is any occurrence that has a probability attached to it—in other words, an event is any outcome where you can say how likely it is to occur.
Probability is measured on a scale of 0 to 1. If an event is impossible, it has a probability of 0. If it’s an absolute certainty, then the probability is 1. A lot of the time, you’ll be dealing with probabilities somewhere in between.
Here are some examples on a probability scale.
Can you see how probability relates to roulette?
If you know how likely the ball is to land on a particular number or color, you have some way of judging whether or not you should place a particular bet. It’s useful knowledge if you want to win at roulette.
Let’s try working out a probability for roulette, the probability of the ball landing on 7. We’ll guide you every step of the way.
1. Look at your roulette board. How many pockets are there for the ball to land in?
2. How many pockets are there for the number 7?
3. To work out the probability of getting a 7, take your answer to question 2 and divide it by your answer to question 1. What do you get?
4. Mark the probability on the scale below. How would you describe how likely it is that you’ll get a 7?
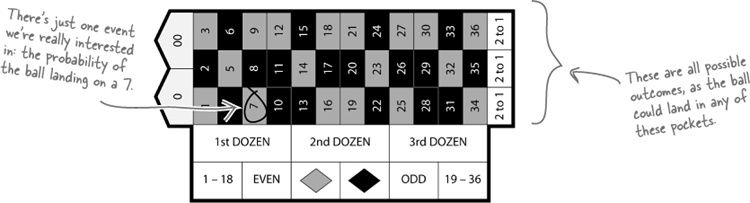
Find roulette probabilities
Let’s take a closer look at how we calculated that probability.
Here are all the possible outcomes from spinning the roulette wheel. The thing we’re really interested in is winning the bet—that is, the ball landing on a 7.
To find the probability of winning, we take the number of ways of winning the bet and divide by the number of possible outcomes like this:
We can write this in a more general way, too. For the probability of any event A:
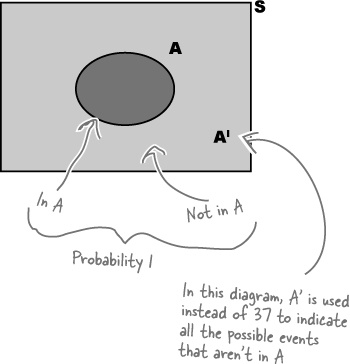
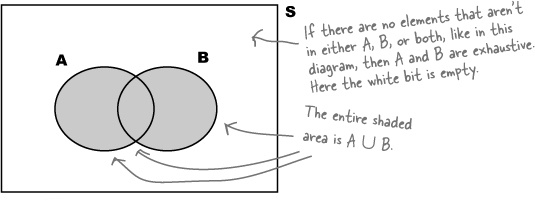
S is known as the possibility space, or sample space. It’s a shorthand way of referring to all of the possible outcomes. Possible events are all subsets of S.
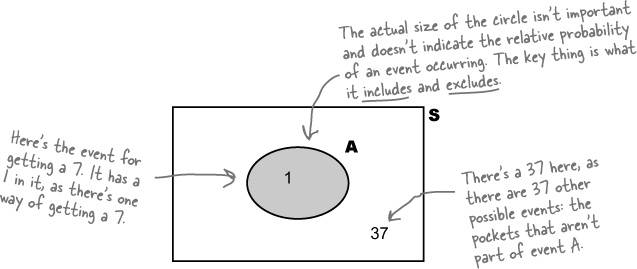
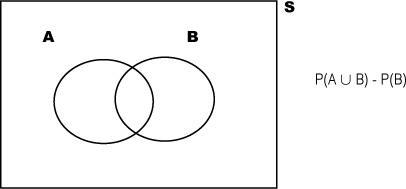
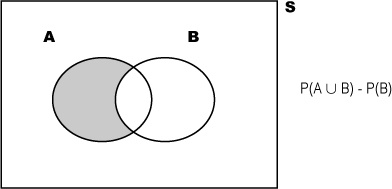
You can visualize probabilities with a Venn diagram
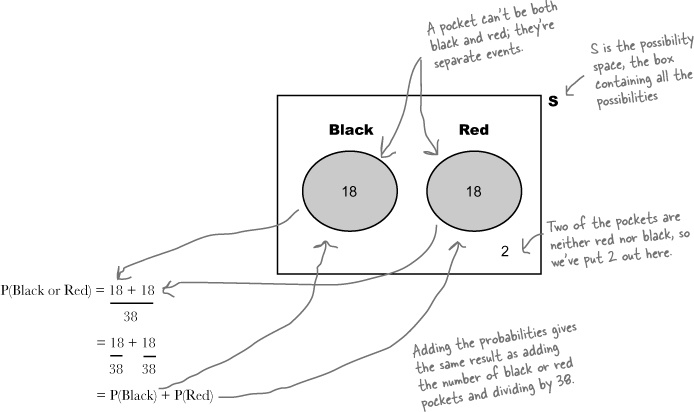
Probabilities can quickly get complicated, so it’s often very useful to have some way of visualizing them. One way of doing so is to draw a box representing the possibility space S, and then draw circles for each relevant event. This sort of diagram is known as a Venn diagram. Here’s a Venn diagram for our roulette problem, where A is the event of getting a 7.
Very often, the numbers themselves aren’t shown on the Venn diagram. Instead of numbers, you have the option of using the actual probabilities of each event in the diagram. It all depends on what kind of information you need to help you solve the problem.
Complementary events
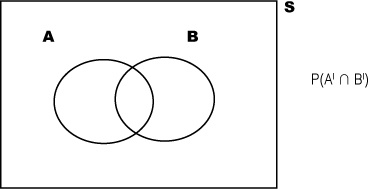
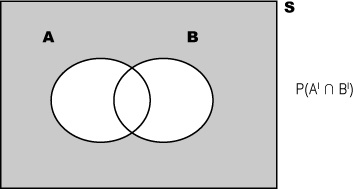
There’s a shorthand way of indicating the event that A does not occur—AI. AI is known as the complementary event of A.
There’s a clever way of calculating P(AI). AI covers every possibility that’s not in event A, so between them, A and AI must cover every eventuality. If something’s in A, it can’t be in AI, and if something’s not in A, it must be in AI. This means that if you add P(A) and P(AI) together, you get 1. In other words, there’s a 100% chance that something will be in either A or AI. This gives us
P(A) + P(AI) = 1
or
P(AI) = 1 – P(A)
Your job is to imagine you’re the croupier and work out the probabilities of various events. For each event below, write down the probability of a successful outcome.
P(9) | P(Green) |
P(Black) | P(38) |
Your job was to imagine you’re the croupier and work out the probabilities of various events. For each event you should have written down the probability of a successful outcome.
P(9) | P(Green) |
The probability of getting a 9 is exactly the same as getting a 7, as there’s an equal chance of the ball falling into each pocket. | 2 of the pockets are green, and there are 38 pockets total, so: |
P(Black) | P(38) |
18 of the pockets are black, and there are 38 pockets, so: | This event is actually impossible—there is no pocket labeled 38. Therefore, the probability is 0. |
It’s time to play!
A game of roulette is just about to begin.
Look at the events on the previous page. We’ll place a bet on the one that’s most likely to occur—that the ball will land in a black pocket.
And the winning number is...
Oh dear! Even though our most likely probability was that the ball would land in a black pocket, it actually landed in the green 0 pocket. You lose some of your chips.
Probabilities are only indications of how likely events are; they’re not guarantees.
The important thing to remember is that a probability indicates a long-term trend only. If you were to play roulette thousands of times, you would expect the ball to land in a black pocket in 18/38 spins, approximately 47% of the time, and a green pocket in 2/38 spins, or 5% of the time. Even though you’d expect the ball to land in a green pocket relatively infrequently, that doesn’t mean it can’t happen.
No matter how unlikely an event is, if it’s not impossible, it can still happen.
Let’s bet on an even more likely event
Let’s look at the probability of an event that should be more likely to happen. Instead of betting that the ball will land in a black pocket, let’s bet that the ball will land in a black or a red pocket. To work out the probability, all we have to do is count how many pockets are red or black, then divide by the number of pockets. Sound easy enough?
We can use the probabilities we already know to work out the one we don’t know.
Take a look at your roulette board. There are only three colors for the ball to land on: red, black, or green. As we’ve already worked out what P(Green) is, we can use this value to find our probability without having to count all those black and red pockets.
P(Black or Red) | = P(GreenI) |
= 1 – P(Green) | |
= 1 – 0.053 | |
= 0.947 (to 3 decimal places) |
You can also add probabilities
There’s yet another way of working out this sort of probability. If we know P(Black) and P(Red), we can find the probability of getting a black or red by adding these two probabilities together. Let’s see.
In this case, adding the probabilities gives exactly the same result as counting all the red or black pockets and dividing by 38.
Time for another bet
Now that you’re getting the hang of calculating probabilities, let’s try something else. What’s the probability of the ball landing on a black or even pocket?
Sometimes you can add together probabilities, but it doesn’t work in all circumstances.
We might not be able to count on being able to do this probability calculation in quite the same way as the previous one. Try the exercise on the next page, and see what happens.
Let’s find the probability of getting a black or even (assume 0 and 00 are not even).
1. What’s the probability of getting a black?
2. What’s the probability of getting an even number?
3. What do you get if you add these two probabilities together?
4. Finally, use your roulette board to count all the holes that are either black or even, then divide by the total number of holes. What do you get?
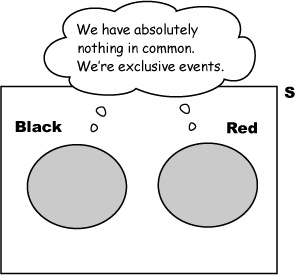
Exclusive events and intersecting events
When we were working out the probability of the ball landing in a black or red pocket, we were dealing with two separate events, the ball landing in a black pocket and the ball landing in a red pocket. These two events are mutually exclusive because it’s impossible for the ball to land in a pocket that’s both black and red.
If two events are mutually exclusive, only one of the two can occur.
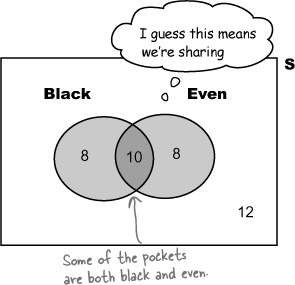
What about the black and even events? This time the events aren’t mutually exclusive. It’s possible that the ball could land in a pocket that’s both black and even. The two events intersect.
If two events intersect, it’s possible they can occur simultaneously.
Problems at the intersection
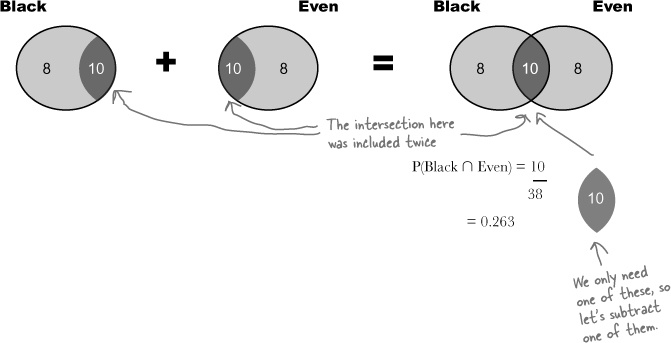
Calculating the probability of getting a black or even went wrong because we included black and even pockets twice. Here’s what happened.
First of all, we found the probability of getting a black pocket and the probability of getting an even number.
When we added the two probabilities together, we counted the probability of getting a black and even pocket twice.
To get the correct answer, we need to subtract the probability of getting both black and even. This gives us
P(Black or Even) = P(Black) + P(Even) – P(Black and Even)
We can now substitute in the values we just calculated to find P(Black or Even):
P(Black or Even) = 18/38 + 18/38 – 10/38 = 26/38 = 0.684
Some more notation
There’s a more general way of writing this using some more math shorthand.
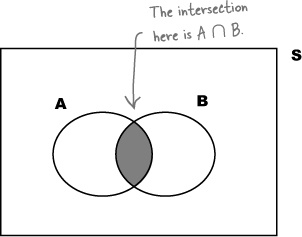
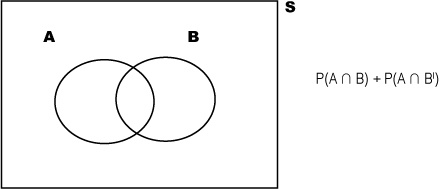
First of all, we can use the notation A ∩ B to refer to the intersection between A and B. You can think of this symbol as meaning “and.” It takes the common elements of events.
A ∪ B, on the other hand, means the union of A and B. It includes all of the elements in A and also those in B. You can think of it as meaning “or.”
If A ∪ B =1, then A and B are said to be exhaustive. Between them, they make up the whole of S. They exhaust all possibilities.
It’s not actually that different.
Mutually exclusive events have no elements in common with each other. If you have two mutually exclusive events, the probability of getting A and B is actually 0—so P(A ∩ B) = 0. Let’s revisit our black-or-red example. In this bet, getting a red pocket on the roulette wheel and getting a black pocket are mutually exclusive events, as a pocket can’t be both red and black. This means that P(Black ∩ Red) = 0, so that part of the equation just disappears.
Watch it!
There’s a difference between exclusive and exhaustive.
If events A and B are exclusive, then
P(A ∩ B) = 0
If events A and B are exhaustive, then
P(A ∪ B) = 1
Your job is to play like you’re the probability and shade in the area that represents each of the following probabilities on the Venn diagrams.
Your job was to play like you’re the probability and shade in the area that represents each of the probabilities on the Venn diagrams.
Vital Statistics: A or B
To find the probability of getting event A or B, use
P(A ∪ B) = P(A) + P(B) – P(A ∩ B)
∪ means OR
∩ means AND
50 sports enthusiasts at the Head First Health Club are asked whether they play baseball, football or basketball. 10 only play baseball. 12 only play football. 18 only play basketball. 6 play baseball and basketball but not football. 4 play football and basketball but not baseball.
Draw a Venn diagram for this probability space. How many enthusiasts play baseball in total? How many play basketball? How many play football?
Are any sports’ rosters mutually exclusive? Which sports are exhaustive (fill up the possibility space)?
By adding up the values in each circle in the Venn diagram, we can determine that there are 16 total baseball players, 28 total basketball players, and 16 total football players.
The baseball and football events are mutually exclusive. Nobody plays both baseball and football, so P(Baseball ∩ Football) = 0
The events for baseball, football, and basketball are exhaustive. Together, they fill the entire possibility space, so P(Baseball ∪ Football ∪ Basketball) = 1
Another unlucky spin...
We know that the probability of the ball landing on black or even is 0.684, but, unfortunately, the ball landed on 23, which is red and odd.
...but it’s time for another bet
Even with the odds in our favor, we’ve been unlucky with the outcomes at the roulette table. The croupier decides to take pity on us and offers a little inside information. After she spins the roulette wheel, she’ll give us a clue about where the ball landed, and we’ll work out the probability based on what she tells us.
Should we take this bet?
How does the probability of getting even given that we know the ball landed in a black pocket compare to our last bet that the ball would land on black or even. Let’s figure it out.
Conditions apply
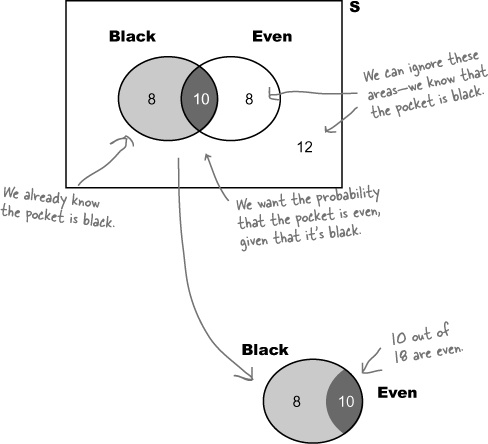
The croupier says the ball has landed in a black pocket. What’s the probability that the pocket is also even?
This is a slightly different problem
We don’t want to find the probability of getting a pocket that is both black and even, out of all possible pockets. Instead, we want to find the probability that the pocket is even, given that we already know it’s black.
In other words, we want to find out how many pockets are even out of all the black ones. Out of the 18 black pockets, 10 of them are even, so
It turns out that even with some inside information, our odds are actually lower than before. The probability of even given black is actually less than the probability of black or even.
However, a probability of 0.556 is still better than 50% odds, so this is still a pretty good bet. Let’s go for it.
Find conditional probabilities
So how can we generalize this sort of problem? First of all, we need some more notation to represent conditional probabilities, which measure the probability of one event occurring relative to another occurring.
If we want to express the probability of one event happening given another one has already happened, we use the “|” symbol to mean “given.” Instead of saying “the probability of event A occurring given event B,” we can shorten it to say
P(A | B)
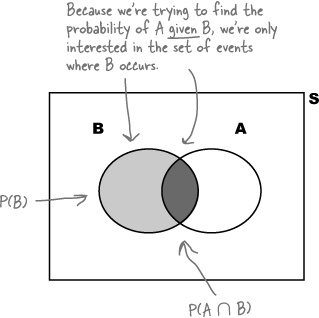
So now we need a general way of calculating P(A | B). What we’re interested in is the number of outcomes where both A and B occur, divided by all the B outcomes. Looking at the Venn diagram, we get:
We can rewrite this equation to give us a way of finding P(A ∩ B)
P(A ∩ B) = P(A | B) × P(B)
It doesn’t end there. Another way of writing P(A ∩ B) is P(B ∩ A). This means that we can rewrite the formula as
P(B ∩ A) = P(B | A) × P(A)
In other words, just flip around the A and the B.
Venn diagrams aren’t always the best way of visualizing conditional probability.
Don’t worry, there’s another sort of diagram you can use—a probability tree.
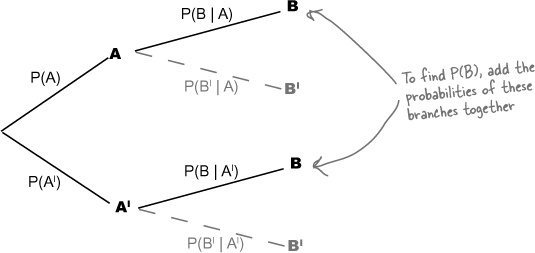
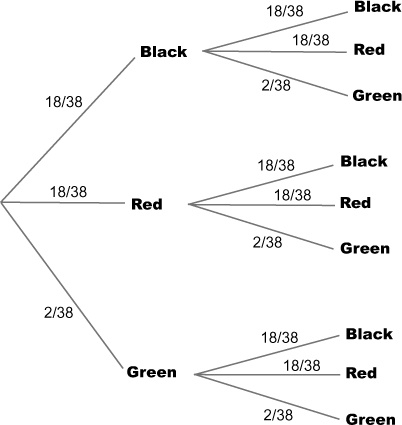
You can visualize conditional probabilities with a probability tree
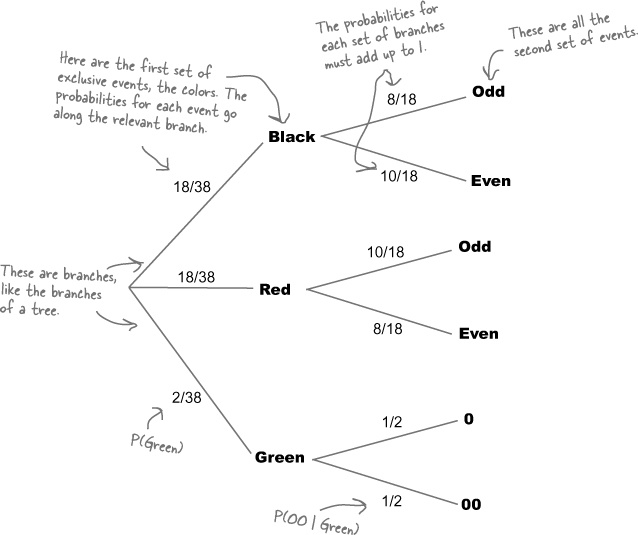
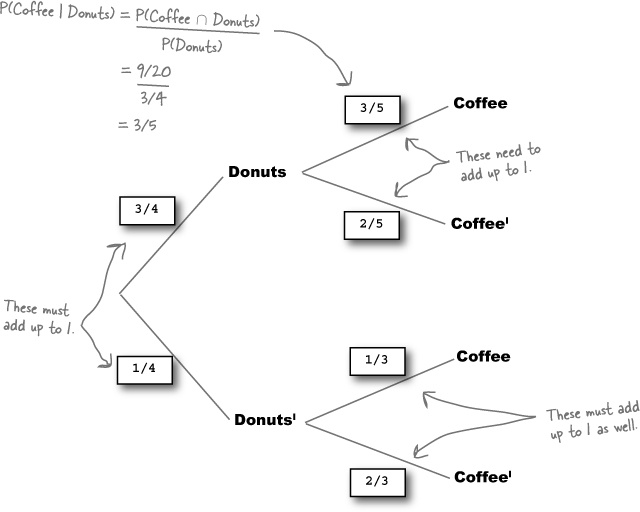
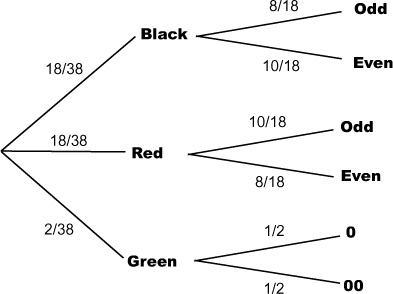
It’s not always easy to visualize conditional probabilities with Venn diagrams, but there’s another sort of diagram that really comes in handy in this situation—the probability tree. Here’s a probability tree for our problem with the roulette wheel, showing the probabilities for getting different colored and odd or even pockets.
The first set of branches shows the probability of each outcome, so the probability of getting a black is 18/38, or 0.474. The second set of branches shows the probability of outcomes given the outcome of the branch it is linked to. The probability of getting an odd pocket given we know it’s black is 8/18, or 0.444.
Trees also help you calculate conditional probabilities
Probability trees don’t just help you visualize probabilities; they can help you to calculate them, too.
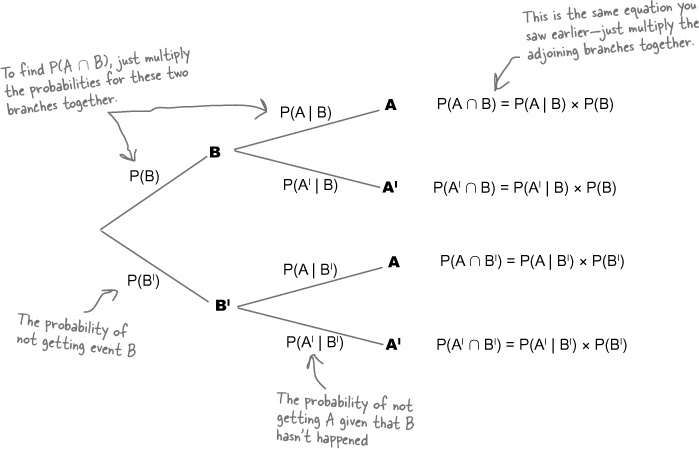
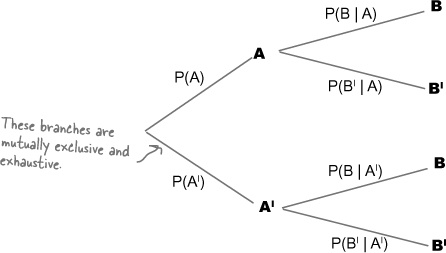
Let’s take a general look at how you can do this. Here’s another probability tree, this time with a different number of branches. It shows two levels of events: A and AI and B and BI. AI refers to every possibility not covered by A, and BI refers to every possibility not covered by B.
You can find probabilities involving intersections by multiplying the probabilities of linked branches together. As an example, suppose you want to find P(A ∩ B). You can find this by multiplying P(B) and P(A | B) together. In other words, you multiply the probability on the first level B branch with the probability on the second level A branch.
Using probability trees gives you the same results you saw earlier, and it’s up to you whether you use them or not. Probability trees can be time-consuming to draw, but they offer you a way of visualizing conditional probabilities.
Duncan’s Donuts are looking into the probabilities of their customers buying donuts and coffee. They drew up a probability tree to show the probabilities, but in a sudden gust of wind, they all fell off. Your task is to pin the probabilities back on the tree. Here are some clues to help you.
P(Donuts) = 3/4 | P(Coffee | DonutsI) = 1/3 | P(Donuts ∩ Coffee) = 9/20 |
Try and work out the different levels of probability that you need. As an example, if you’re given a probability for P(A | B), you’ll probably need the first level to cover B, and the second level A.
2. Fill in what you know
If you’re given a series of probabilities, put them onto the tree in the relevant position.
3. Remember that each set of branches sums to 1
If you add together the probabilities for all of the branches that fork off from a common point, the sum should equal 1. Remember that P(A) = 1 – P(AI).
4. Remember your formula
You should be able to find most other probabilities by using
Duncan’s Donuts are looking into the probabilities of their customers buying Donuts and Coffee. They drew up a probability tree to show the probabilities, but in a sudden gust of wind they all fell off. Your task is to pin the probabilities back on the tree. Here are some clues to help you.
P(Donuts) = 3/4 | P(Coffee | DonutsI) = 1/3 | P(Donuts ∩ Coffee) = 9/20 |
Bad luck!
You placed a bet that the ball would land in an even pocket given we’ve been told it’s black. Unfortunately, the ball landed in pocket 17, so you lose a few more chips.
Maybe we can win some chips back with another bet. This time, the croupier says that the ball has landed in an even pocket. What’s the probability that the pocket is also black?
We can reuse the probability calculations we already did.
Our previous task was to figure out P(Even | Black), and we can use the probabilities we found solving that problem to calculate P(Black | Even). Here’s the probability tree we used before:
We can find P(Black l Even) using the probabilities we already have
So how do we find P(Black | Even)? There’s still a way of calculating this using the probabilities we already have even if it’s not immediately obvious from the probability tree. All we have to do is look at the probabilities we already have, and use these to somehow calculate the probabilities we don’t yet know.
Let’s start off by looking at the overall probability we need to find, P(Black | Even).
Using the formula for finding conditional probabilities, we have
If we can find what the probabilities of P(Black ∩ Even) and P(Even) are, we’ll be able to use these in the formula to calculate P(Black | Even). All we need is some mechanism for finding these probabilities.
Sound difficult? Don’t worry, we’ll guide you through how to do it.
Use the probabilities you have to calculate the probabilities you need
Step 1: Finding P(Black ∩ Even)
Let’s start off with the first part of the formula, P(Black ∩ Even).
So where does this get us?
We want to find the probability P(Black | Even). We can do this by evaluating
Brain Power
Take another look at the probability tree in So where does this get us?. How do you think we can use it to find P(Even)?
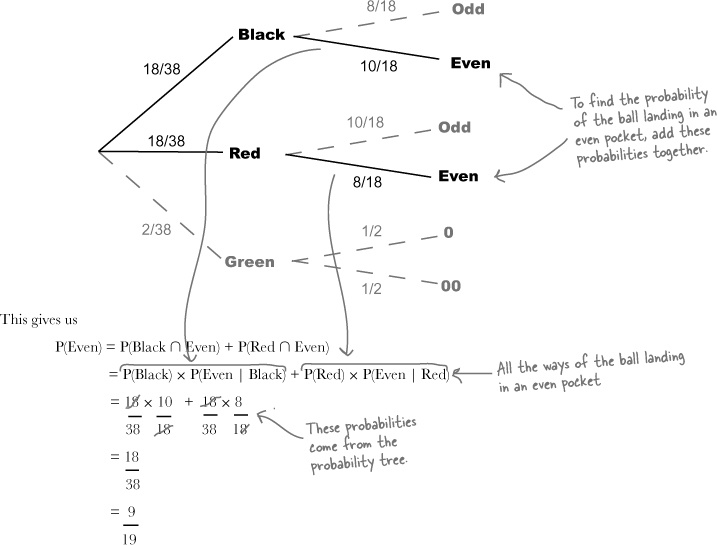
Step 2: Finding P(Even)
The next step is to find the probability of the ball landing in an even pocket, P(Even). We can find this by considering all the ways in which this could happen.
A ball can land in an even pocket by landing in either a pocket that’s both black and even, or in a pocket that’s both red and even. These are all the possible ways in which a ball can land in an even pocket.
This means that we find P(Even) by adding together P(Black ∩ Even) and P(Red ∩ Even). In other words, we add the probability of the pocket being both black and even to the probability of it being both red and even. The relevant branches are highlighted on the probability tree.
Step 3: Finding P(Black l Even)
Can you remember our original problem? We wanted to find P(Black | Even) where
Putting these together means that we can calculate P(Black | Even) using probabilities from the probability tree
This means that we now have a way of finding new conditional probabilities using probabilities we already know—something that can help with more complicated probability problems.
Let’s look at how this works in general.
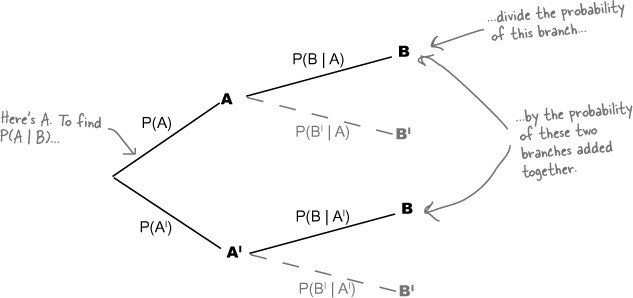
These results can be generalized to other problems
Imagine you have a probability tree showing events A and B like this, and assume you know the probability on each of the branches.
Now imagine you want to find P(A | B), and the information shown on the branches above is all the information that you have. How can you use the probabilities you have to work out P(A | B)?
We can start with the formula we had before:
Now we can find P(A ∩ B) using the probabilities we have on the probability tree. In other words, we can calculate P(A ∩ B) using
P(A ∩ B) = P(A) × P(B | A)
But how do we find P(B)?
Use the Law of Total Probability to find P(B)
To find P(B), we use the same process that we used to find P(Even) earlier; we need to add together the probabilities of all the different ways in which the event we want can possibly happen.
There are two ways in which even B can occur: either with event A, or without it. This means that we can find P(B) using:
P(B) = P(A ∩ B) + P(AI ∩ B)
We can rewrite this in terms of the probabilities we already know from the probability tree. This means that we can use:
P(A ∩ B) = P(A) × P(B | A)
P(AI ∩ B) = P(AI) × P(B | AI)
This gives us:
P(B) = P(A) × P(B | A) + P(AI) × P(B | AI)
This is sometimes known as the Law of Total Probability, as it gives a way of finding the total probability of a particular event based on conditional probabilities.
Now that we have expressions for P(A ∩ B) and P(B), we can put them together to come up with an expression for P(A | B).
Introducing Bayes’ Theorem
We started off by wanting to find P(A | B) based on probabilities we already know from a probability tree. We already know P(A), and we also know P(B | A) and P(B | AI). What we need is a general expression for finding conditional probabilities that are the reverse of what we already know, in other words P(A | B).
We started off with:
Relax
Bayes’ Theorem is one of the most difficult aspects of probability.
Don’t worry if it looks complicated—this is as tough as it’s going to get. And even though the formula is tricky, visualizing the problem can help.
This is called Bayes’ Theorem. It gives you a means of finding reverse conditional probabilities, which is really useful if you don’t know every probability up front.
The Manic Mango games company is testing two brand-new games. They’ve asked a group of volunteers to choose the game they most want to play, and then tell them how satisfied they were with game play afterwards.
80 percent of the volunteers chose Game 1, and 20 percent chose Game 2. Out of the Game 1 players, 60 percent enjoyed the game and 40 percent didn’t. For Game 2, 70 percent of the players enjoyed the game and 30 percent didn’t.
Your first task is to fill in the probability tree for this scenario.
Manic Mango selects one of the volunteers at random to ask if she enjoyed playing the game, and she says she did. Given that the volunteer enjoyed playing the game, what’s the probability that she played game 2? Use Bayes’ Theorem.
We need to use Bayes’ Theorem to find P(Game 2 | Satisfied). This means we need to use
Let’s start with P(Game 2) P(Satisfied | Game 2)
We’ve been told that P(Game 2) = 0.2 and P(Satisfied | Game 2) = 0.7. This means that
P(Game 2) P(Satisfied | Game 2) | = 0.2 x 0.7 |
= 0.14 |
The next thing we need to find is P(Game 2) P(Dissatisfied | Game 2). We’ve been told that P(Dissatisfied | Game 2) = 0.3, and we’ve already seen that P(Game 2) = 0.2. This gives us
P(Game 2) P(Dissatisfied | Game 2) | = 0.2 x 0.2 |
= 0.06 |
Substituting this into the formula for Bayes’ Theorem gives us
We have a winner!
Congratulations, this time the ball landed on 10, a pocket that’s both black and even. You’ve won back some chips.
It’s time for one last bet
Before you leave the roulette table, the croupier has offered you a great deal for your final bet, triple or nothing. If you bet that the ball lands in a black pocket twice in a row, you could win back all of your chips.
Here’s the probability tree. Notice that the probabilities for landing on two black pockets in a row are a bit different than they were in our probability tree in Bad luck!, where we were trying to calculate the likelihood of getting an even pocket given that we knew the pocket was black.
If events affect each other, they are dependent
The probability of getting black followed by black is a slightly different problem from the probability of getting an even pocket given we already know it’s black. Take a look at the equation for this probability:
P(Even | Black) = 10/18 = 0.556
For P(Even | Black), the probability of getting an even pocket is affected by the event of getting a black. We already know that the ball has landed in a black pocket, so we use this knowledge to work out the probability. We look at how many of the pockets are even out of all the black pockets.
If we didn’t know that the ball had landed on a black pocket, the probability would be different. To work out P(Even), we look at how many pockets are even out of all the pockets
P(Even) = 18/38 = 0.474
P(Even | Black) gives a different result from P(Even). In other words, the knowledge we have that the pocket is black changes the probability. These two events are said to be dependent.
In general terms, events A and B are said to be dependent if P(A | B) is different from P(A). It’s a way of saying that the probabilities of A and B are affected by each other.
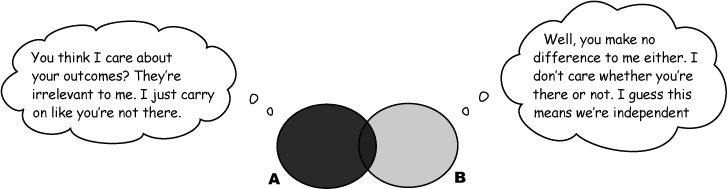
If events do not affect each other, they are independent
Not all events are dependent. Sometimes events remain completely unaffected by each other, and the probability of an event occurring remains the same irrespective of whether the other event happens or not. As an example, take a look at the probabilities of P(Black) and P(Black | Black). What do you notice?
P(Black) = 18/38 = 0.474
P(Black | Black) = 18/38 = 0.474
These two probabilities have the same value. In other words, the event of getting a black pocket in this game has no bearing on the probability of getting a black pocket in the next game. These events are independent.
Independent events aren’t affected by each other. They don’t influence each other’s probabilities in any way at all. If one event occurs, the probability of the other occurring remains exactly the same.
If events A and B are independent, then the probability of event A is unaffected by event B. In other words
P(A | B) = P(A)
for independent events.
We can also use this as a test for independence. If you have two events A and B where P(A | B) = P(A), then the events A and B must be independent.
More on calculating probability for independent events
It’s easier to work out other probabilities for independent events too, for example P(A ∩ B).
We already know that
If A and B are independent, P(A | B) is the same as P(A). This means that
or
P(A ∩ B) = P(A) × P(B)
Watch it!
If A and B are mutually exclusive, they can’t be independent, and if A and B are independent, they can’t be mutually exclusive.
If A and B are mutually exclusive, then if event A occurs, event B cannot. This means that the outcome of A affects the outcome of B, and so they’re dependent.
Similarly if A and B are independent, they can’t be mutually exclusive.
for independent events. In other words, if two events are independent, then you can work out the probability of getting both events A and B by multiplying their individual probabilities together.
Vital Statistics: Independence
If two events A and B are independent, then
P(A | B) = P(A)
If this holds for any two events, then the events must be independent. Also
P(A ∩ B) = P(A) x P(B)
Tonight’s talk: Dependent and Independent discuss their differences
|
|
Independent, glad you could show up. I’ve been wanting to catch up with you for some time. | |
Really, Dependent? How come? | |
Well, I hear you keep getting fledgling statisticians into trouble. They’re doing fine until you show up, and then, whoa, wrong probabilities all over the place! That ∩ guy has a particularly poor opinion of you. | |
I’m a little hurt that ∩’s been saying bad things about me; I thought I made life easy for him. You want to work out the probability of getting two independent events? Easy! Just multiply the probabilities for the two events together and job done. | |
It’s that simplistic attitude of yours that gets people into trouble. They think, “Hey, that Independent guy looks easy. I’ll just use him for this probability.” The next thing you know, ∩ has his probabilities all in a twist. That’s just not the right way of dealing with dependent events. | |
You’re blowing this all out of proportion. Even if people do decide to use me instead of you, I don’t see that it can make all that much difference. | |
You don’t understand the seriousness of the situation. If people use your way of calculating ∩’s probability, and the events are dependent, they’re guaranteed to get the wrong answer. That’s just not good enough. For dependent events, you only get the right answer if you take that | guy into account—he’s a given. | |
I can’t say I pay all that much attention to him. With independent events, probabilities just turn out the same. | |
You’re doing it again; you’re oversimplifying things. Well, I’ve had enough. I think that people need to think of me first instead of you; that would sort out all of these problems. | |
Yeah? Like how? | |
By really thinking through whether events are dependent or not. Let me give you an example. Suppose you have a deck of 52 cards, and thirteen of them are diamonds. Imagine you choose a card at random and it’s a diamond. What would be the probability of that happening? | |
That’s easy. It’s 13/52, or 1/4. | |
What if you pick out a second card? What’s the probability of pulling out a second diamond? | |
It’s the same isn’t it? 1/4. | |
No! The events are dependent. You can no longer say there are 13 diamonds in a pack of 52 cards. You’ve just removed one diamond, so there are 12 diamonds left out of 51 cards. The probability drops to 12/51, or 4/17. | |
Not fair, I assumed you put the first card back! That would have meant the probability of getting a diamond would have been the same as before, and I would have been right. The events would have been independent. | |
But they weren’t. When people think about you first, it leads them towards making all sorts of inappropriate assumptions. No wonder ∩ gets so messed up. | |
Well, thanks for the chat, Dependent, I’m glad we had a chance to sort things out. | |
Think nothing of it. Just make sure you think things through a bit more carefully next time. |
Here are a bunch of situations and events. Your task is to say which of these are dependent, and which are independent.
Dependent | Independent | |
Throwing a coin and getting heads twice in a row. | ||
Removing socks from a drawer until you find a matching pair. | ||
Choosing chocolates at random from a box and picking dark chocolates twice in a row. | ||
Choosing a card from a deck of cards, and then choosing another one. | ||
Choosing a card from a deck of cards, putting the card back in the deck, and then choosing another one. | ||
The event of getting rain given it’s a Thursday. |
Here are a bunch of situations and events. Your task was to say which of these are dependent, and which are independent.
Dependent | Independent | |
Throwing a coin and getting heads twice in a row. | ||
Removing socks from a drawer until you find a matching pair. | ||
Choosing chocolates at random from a box and picking dark chocolates twice in a row. | ||
Choosing a card from a deck of cards, and then choosing another one. | ||
Choosing a card from a deck of cards, putting the card back in the deck, and then choosing another one. | ||
The event of getting rain given it’s a Thursday. |
Winner! Winner!
On both spins of the wheel, the ball landed on 30, a red square, and you doubled your winnings.
You’ve learned a lot about probability over at Fat Dan’s roulette table, and you’ll find this knowledge will come in handy for what’s ahead at the casino. It’s a pity you didn’t win enough chips to take any home with you, though.
Besides the chances of winning, you also need to know how much you stand to win in order to decide if the bet is worth the risk.
Betting on an event that has a very low probability may be worth it if the payoff is high enough to compensate you for the risk. In the next chapter, we’ll look at how to factor these payoffs into our probability calculations to help us make more informed betting decisions.
Three absent-minded friends decide to go out for a meal, but they forget where they’re going to meet. Fred decides to throw a coin. If it lands heads, he’ll go to the diner; tails, and he’ll go to the Italian restaurant. George throws a coin, too; heads, it’s the Italian restaurant; tails, it’s the diner. Ron decides he’ll just go to the Italian restaurant because he likes the food.
What’s the probability all three friends meet? What’s the probability one of them eats alone?
If all friends meet, it must be at the Italian restaurant. We need to find
P(Ron Italian ∩ Fred Italian ∩ George Italian)
= 1 x 0.5 x 0.5 = 0.25
I person eats alone if Fred and George go to the Diner. Fred goes to the Diner while George goes to Italian restaurant, or George goes to the Diner and Fred gets Italian..
(0.5 x 0.5) + (0.5 x 0.5) + (0.5 x 0.5) = 0.75
Get Head First Statistics now with the O’Reilly learning platform.
O’Reilly members experience books, live events, courses curated by job role, and more from O’Reilly and nearly 200 top publishers.
