MySQL’s architecture is very different from that of other database servers, and makes it useful for a wide range of purposes. MySQL is not perfect, but it is flexible enough to work well in very demanding environments, such as web applications. At the same time, MySQL can power embedded applications, data warehouses, content indexing and delivery software, highly available redundant systems, online transaction processing (OLTP), and much more.
To get the most from MySQL, you need to understand its design so that you can work with it, not against it. MySQL is flexible in many ways. For example, you can configure it to run well on a wide range of hardware, and it supports a variety of data types. However, MySQL’s most unusual and important feature is its storage-engine architecture, whose design separates query processing and other server tasks from data storage and retrieval. In MySQL 5.1, you can even load storage engines as runtime plug-ins. This separation of concerns lets you choose, on a per-table basis, how your data is stored and what performance, features, and other characteristics you want.
This chapter provides a high-level overview of the MySQL server architecture, the major differences between the storage engines, and why those differences are important. We’ve tried to explain MySQL by simplifying the details and showing examples. This discussion will be useful for those new to database servers as well as readers who are experts with other database servers.
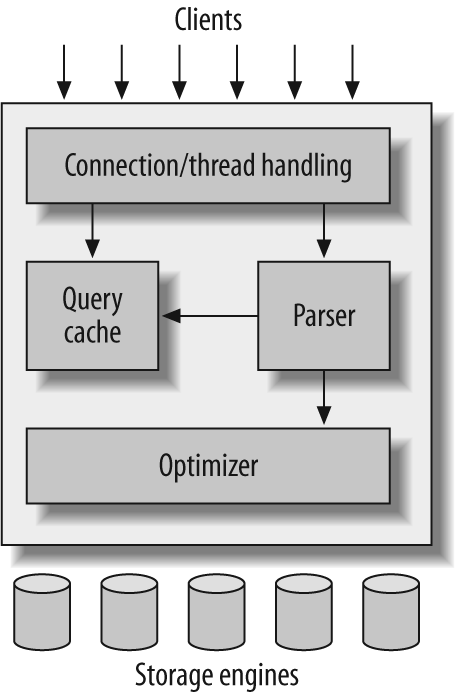
A good mental picture of how MySQL’s components work together will help you understand the server. Figure 1-1 shows a logical view of MySQL’s architecture.
The topmost layer contains the services that aren’t unique to MySQL. They’re services most network-based client/server tools or servers need: connection handling, authentication, security, and so forth.
The second layer is where things get interesting. Much of MySQL’s brains are here, including the code for query parsing, analysis, optimization, caching, and all the built-in functions (e.g., dates, times, math, and encryption). Any functionality provided across storage engines lives at this level: stored procedures, triggers, and views, for example.
The third layer contains the storage engines. They are responsible for storing and retrieving all data stored “in” MySQL. Like the various filesystems available for GNU/Linux, each storage engine has its own benefits and drawbacks. The server communicates with them through the storage engine API. This interface hides differences between storage engines and makes them largely transparent at the query layer. The API contains a couple of dozen low-level functions that perform operations such as “begin a transaction” or “fetch the row that has this primary key.” The storage engines don’t parse SQL[4] or communicate with each other; they simply respond to requests from the server.
Each client connection gets its own thread within the server process. The connection’s queries execute within that single thread, which in turn resides on one core or CPU. The server caches threads, so they don’t need to be created and destroyed for each new connection.[5]
When clients (applications) connect to the MySQL server, the
server needs to authenticate them. Authentication is based on username, originating host,
and password. X.509 certificates can also be used across an Secure
Sockets Layer (SSL) connection. Once a client has connected, the
server verifies whether the client has privileges for each query it
issues (e.g., whether the client is allowed to issue a SELECT statement that accesses the Country table in the world database). We cover these topics in
detail in Chapter 12.
MySQL parses queries to create an internal structure (the parse tree), and then applies a variety of optimizations. These may include rewriting the query, determining the order in which it will read tables, choosing which indexes to use, and so on. You can pass hints to the optimizer through special keywords in the query, affecting its decision-making process. You can also ask the server to explain various aspects of optimization. This lets you know what decisions the server is making and gives you a reference point for reworking queries, schemas, and settings to make everything run as efficiently as possible. We discuss the optimizer in much more detail in Chapter 4.
The optimizer does not really care what storage engine a particular table uses, but the storage engine does affect how the server optimizes the query. The optimizer asks the storage engine about some of its capabilities and the cost of certain operations, and for statistics on the table data. For instance, some storage engines support index types that can be helpful to certain queries. You can read more about indexing and schema optimization in Chapter 3.
Before even parsing the query, though, the server consults the
query cache, which can store only SELECT statements, along with their result
sets. If anyone issues a query that’s identical to one already in the
cache, the server doesn’t need to parse, optimize, or execute the
query at all—it can simply pass back the stored result set! We discuss
the query cache at length in “The MySQL Query Cache” on The MySQL Query Cache.
Anytime more than one query needs to change data at the same time, the problem of concurrency control arises. For our purposes in this chapter, MySQL has to do this at two levels: the server level and the storage engine level. Concurrency control is a big topic to which a large body of theoretical literature is devoted, but this book isn’t about theory or even about MySQL internals. Thus, we will just give you a simplified overview of how MySQL deals with concurrent readers and writers, so you have the context you need for the rest of this chapter.
We’ll use an email box on a Unix system as an example. The classic mbox file format is very simple. All the messages in an mbox mailbox are concatenated together, one after another. This makes it very easy to read and parse mail messages. It also makes mail delivery easy: just append a new message to the end of the file.
But what happens when two processes try to deliver messages at the same time to the same mailbox? Clearly that could corrupt the mailbox, leaving two interleaved messages at the end of the mailbox file. Well-behaved mail delivery systems use locking to prevent corruption. If a client attempts a second delivery while the mailbox is locked, it must wait to acquire the lock itself before delivering its message.
This scheme works reasonably well in practice, but it gives no support for concurrency. Because only a single process can change the mailbox at any given time, this approach becomes problematic with a high-volume mailbox.
Reading from the mailbox isn’t as troublesome. There’s nothing wrong with multiple clients reading the same mailbox simultaneously; because they aren’t making changes, nothing is likely to go wrong. But what happens if someone tries to delete message number 25 while programs are reading the mailbox? It depends, but a reader could come away with a corrupted or inconsistent view of the mailbox. So, to be safe, even reading from a mailbox requires special care.
If you think of the mailbox as a database table and each mail message as a row, it’s easy to see that the problem is the same in this context. In many ways, a mailbox is really just a simple database table. Modifying rows in a database table is very similar to removing or changing the content of messages in a mailbox file.
The solution to this classic problem of concurrency control is rather simple. Systems that deal with concurrent read/write access typically implement a locking system that consists of two lock types. These locks are usually known as shared locks and exclusive locks, or read locks and write locks.
Without worrying about the actual locking technology, we can describe the concept as follows. Read locks on a resource are shared, or mutually nonblocking: many clients may read from a resource at the same time and not interfere with each other. Write locks, on the other hand, are exclusive—i.e., they block both read locks and other write locks—because the only safe policy is to have a single client writing to the resource at given time and to prevent all reads when a client is writing.
In the database world, locking happens all the time: MySQL has to prevent one client from reading a piece of data while another is changing it. It performs this lock management internally in a way that is transparent much of the time.
One way to improve the concurrency of a shared resource is to be more selective about what you lock. Rather than locking the entire resource, lock only the part that contains the data you need to change. Better yet, lock only the exact piece of data you plan to change. Minimizing the amount of data that you lock at any one time lets changes to a given resource occur simultaneously, as long as they don’t conflict with each other.
The problem is locks consume resources. Every lock operation—getting a lock, checking to see whether a lock is free, releasing a lock, and so on—has overhead. If the system spends too much time managing locks instead of storing and retrieving data, performance can suffer.
A locking strategy is a compromise between lock overhead and data safety, and that compromise affects performance. Most commercial database servers don’t give you much choice: you get what is known as row-level locking in your tables, with a variety of often complex ways to give good performance with many locks.
MySQL, on the other hand, does offer choices. Its storage engines can implement their own locking policies and lock granularities. Lock management is a very important decision in storage engine design; fixing the granularity at a certain level can give better performance for certain uses, yet make that engine less suited for other purposes. Because MySQL offers multiple storage engines, it doesn’t require a single general-purpose solution. Let’s have a look at the two most important lock strategies.
The most basic locking strategy available in MySQL, and the one with the lowest overhead, is table locks. A table lock is analogous to the mailbox locks described earlier: it locks the entire table. When a client wishes to write to a table (insert, delete, update, etc.), it acquires a write lock. This keeps all other read and write operations at bay. When nobody is writing, readers can obtain read locks, which don’t conflict with other read locks.
Table locks have variations for good performance in specific
situations. For example, READ
LOCAL table locks allow some types of concurrent write
operations. Write locks also have a higher priority than read locks,
so a request for a write lock will advance to the front of the lock
queue even if readers are already in the queue (write locks can
advance past read locks in the queue, but read locks cannot advance
past write locks).
Although storage engines can manage their own locks, MySQL
itself also uses a variety of locks that are effectively table-level for various
purposes. For instance, the server uses a table-level lock for
statements such as ALTER TABLE,
regardless of the storage engine.
The locking style that offers the greatest concurrency (and carries the greatest overhead) is the use of row locks. Row-level locking, as this strategy is commonly known, is available in the InnoDB and Falcon storage engines, among others. Row locks are implemented in the storage engine, not the server (refer back to the logical architecture diagram if you need to). The server is completely unaware of locks implemented in the storage engines, and, as you’ll see later in this chapter and throughout the book, the storage engines all implement locking in their own ways.
You can’t examine the more advanced features of a database system for very long before transactions enter the mix. A transaction is a group of SQL queries that are treated atomically, as a single unit of work. If the database engine can apply the entire group of queries to a database, it does so, but if any of them can’t be done because of a crash or other reason, none of them is applied. It’s all or nothing.
Little of this section is specific to MySQL. If you’re already familiar with ACID transactions, feel free to skip ahead to “Transactions in MySQL” on Transaction Logging.
A banking application is the classic example of why transactions
are necessary. Imagine a bank’s database with two tables: checking and savings. To move $200 from Jane’s checking
account to her savings account, you need to perform at least three
steps:
Make sure her checking account balance is greater than $200.
Subtract $200 from her checking account balance.
Add $200 to her savings account balance.
The entire operation should be wrapped in a transaction so that if any one of the steps fails, any completed steps can be rolled back.
You start a transaction with the START
TRANSACTION statement and then either make its changes
permanent with COMMIT or discard the
changes with ROLLBACK. So, the SQL
for our sample transaction might look like this:
1 START TRANSACTION; 2 SELECT balance FROM checking WHERE customer_id = 10233276; 3 UPDATE checking SET balance = balance - 200.00 WHERE customer_id = 10233276; 4 UPDATE savings SET balance = balance + 200.00 WHERE customer_id = 10233276; 5 COMMIT;
But transactions alone aren’t the whole story. What happens if the database server crashes while performing line 4? Who knows? The customer probably just lost $200. And what if another process comes along between lines 3 and 4 and removes the entire checking account balance? The bank has given the customer a $200 credit without even knowing it.
Transactions aren’t enough unless the system passes the ACID test. ACID stands for Atomicity, Consistency, Isolation, and Durability. These are tightly related criteria that a well-behaved transaction processing system must meet:
- Atomicity
A transaction must function as a single indivisible unit of work so that the entire transaction is either applied or rolled back. When transactions are atomic, there is no such thing as a partially completed transaction: it’s all or nothing.
- Consistency
The database should always move from one consistent state to the next. In our example, consistency ensures that a crash between lines 3 and 4 doesn’t result in $200 disappearing from the checking account. Because the transaction is never committed, none of the transaction’s changes is ever reflected in the database.
- Isolation
The results of a transaction are usually invisible to other transactions until the transaction is complete. This ensures that if a bank account summary runs after line 3 but before line 4 in our example, it will still see the $200 in the checking account. When we discuss isolation levels, you’ll understand why we said usually invisible.
- Durability
Once committed, a transaction’s changes are permanent. This means the changes must be recorded such that data won’t be lost in a system crash. Durability is a slightly fuzzy concept, however, because there are actually many levels. Some durability strategies provide a stronger safety guarantee than others, and nothing is ever 100% durable. We discuss what durability really means in MySQL in later chapters, especially in “InnoDB I/O Tuning” on InnoDB I/O Tuning.
ACID transactions ensure that banks don’t lose your money. It is generally extremely difficult or impossible to do this with application logic. An ACID-compliant database server has to do all sorts of complicated things you might not realize to provide ACID guarantees.
Just as with increased lock granularity, the downside of this
extra security is that the database server has to do more work. A
database server with ACID transactions also generally requires more CPU
power, memory, and disk space than one without them. As we’ve said
several times, this is where MySQL’s storage engine architecture works
to your advantage. You can decide whether your application needs
transactions. If you don’t really need them, you might be able to get
higher performance with a nontransactional storage engine for some kinds
of queries. You might be able to use LOCK
TABLES to give the level of protection you need without
transactions. It’s all up to you.
Isolation is more complex than it looks. The SQL standard defines four isolation levels, with specific rules for which changes are and aren’t visible inside and outside a transaction. Lower isolation levels typically allow higher concurrency and have lower overhead.
Tip
Each storage engine implements isolation levels slightly differently, and they don’t necessarily match what you might expect if you’re used to another database product (thus, we won’t go into exhaustive detail in this section). You should read the manuals for whichever storage engine you decide to use.
Let’s take a quick look at the four isolation levels:
READ UNCOMMITTEDIn the
READ UNCOMMITTEDisolation level, transactions can view the results of uncommitted transactions. At this level, many problems can occur unless you really, really know what you are doing and have a good reason for doing it. This level is rarely used in practice, because its performance isn’t much better than the other levels, which have many advantages. Reading uncommitted data is also known as a dirty read.READ COMMITTEDThe default isolation level for most database systems (but not MySQL!) is
READ COMMITTED. It satisfies the simple definition of isolation used earlier: a transaction will see only those changes made by transactions that were already committed when it began, and its changes won’t be visible to others until it has committed. This level still allows what’s known as a nonrepeatable read. This means you can run the same statement twice and see different data.REPEATABLE READREPEATABLE READsolves the problems thatREAD UNCOMMITTEDallows. It guarantees that any rows a transaction reads will “look the same” in subsequent reads within the same transaction, but in theory it still allows another tricky problem: phantom reads. Simply put, a phantom read can happen when you select some range of rows, another transaction inserts a new row into the range, and then you select the same range again; you will then see the new “phantom” row. InnoDB and Falcon solve the phantom read problem with multiversion concurrency control, which we explain later in this chapter.REPEATABLE READis MySQL’s default transaction isolation level. The InnoDB and Falcon storage engines respect this setting, which you’ll learn how to change in Chapter 6. Some other storage engines do too, but the choice is up to the engine.SERIALIZABLEThe highest level of isolation,
SERIALIZABLE, solves the phantom read problem by forcing transactions to be ordered so that they can’t possibly conflict. In a nutshell,SERIALIZABLEplaces a lock on every row it reads. At this level, a lot of timeouts and lock contention may occur. We’ve rarely seen people use this isolation level, but your application’s needs may force you to accept the decreased concurrency in favor of the data stability that results.
Table 1-1 summarizes the various isolation levels and the drawbacks associated with each one.
A deadlock is when two or more transactions
are mutually holding and requesting locks on the same resources,
creating a cycle of dependencies. Deadlocks occur when transactions try to lock resources
in a different order. They can happen whenever multiple transactions
lock the same resources. For example, consider these two transactions
running against the StockPrice
table:
- Transaction #1
START TRANSACTION; UPDATE StockPrice SET close = 45.50 WHERE stock_id = 4 and date = '2002-05-01'; UPDATE StockPrice SET close = 19.80 WHERE stock_id = 3 and date = '2002-05-02'; COMMIT;
- Transaction #2
START TRANSACTION; UPDATE StockPrice SET high = 20.12 WHERE stock_id = 3 and date = '2002-05-02'; UPDATE StockPrice SET high = 47.20 WHERE stock_id = 4 and date = '2002-05-01'; COMMIT;
If you’re unlucky, each transaction will execute its first query and update a row of data, locking it in the process. Each transaction will then attempt to update its second row, only to find that it is already locked. The two transactions will wait forever for each other to complete, unless something intervenes to break the deadlock.
To combat this problem, database systems implement various forms of deadlock detection and timeouts. The more sophisticated systems, such as the InnoDB storage engine, will notice circular dependencies and return an error instantly. This is actually a very good thing—otherwise, deadlocks would manifest themselves as very slow queries. Others will give up after the query exceeds a lock wait timeout, which is not so good. The way InnoDB currently handles deadlocks is to roll back the transaction that has the fewest exclusive row locks (an approximate metric for which will be the easiest to roll back).
Lock behavior and order are storage engine-specific, so some storage engines might deadlock on a certain sequence of statements even though others won’t. Deadlocks have a dual nature: some are unavoidable because of true data conflicts, and some are caused by how a storage engine works.
Deadlocks cannot be broken without rolling back one of the transactions, either partially or wholly. They are a fact of life in transactional systems, and your applications should be designed to handle them. Many applications can simply retry their transactions from the beginning.
Transaction logging helps make transactions more efficient. Instead of updating the tables on disk each time a change occurs, the storage engine can change its in-memory copy of the data. This is very fast. The storage engine can then write a record of the change to the transaction log, which is on disk and therefore durable. This is also a relatively fast operation, because appending log events involves sequential I/O in one small area of the disk instead of random I/O in many places. Then, at some later time, a process can update the table on disk. Thus, most storage engines that use this technique (known as write-ahead logging) end up writing the changes to disk twice.[6]
If there’s a crash after the update is written to the transaction log but before the changes are made to the data itself, the storage engine can still recover the changes upon restart. The recovery method varies between storage engines.
MySQL AB provides three transactional storage engines: InnoDB, NDB Cluster, and Falcon. Several third-party engines are also available; the best-known engines right now are solidDB and PBXT. We discuss some specific properties of each engine in the next section.
MySQL operates in AUTOCOMMIT mode by default. This means
that unless you’ve explicitly begun a transaction, it automatically
executes each query in a separate transaction. You can enable or
disable AUTOCOMMIT for the
current connection by setting a variable:
mysql>SHOW VARIABLES LIKE 'AUTOCOMMIT';+---------------+-------+ | Variable_name | Value | +---------------+-------+ | autocommit | ON | +---------------+-------+ 1 row in set (0.00 sec) mysql>SET AUTOCOMMIT = 1;
The values 1 and ON are equivalent, as are 0 and OFF. When you run with AUTOCOMMIT=0,
you are always in a transaction, until you issue a COMMIT or ROLLBACK. MySQL then starts a new
transaction immediately. Changing the value of AUTOCOMMIT has no effect on
nontransactional tables, such as MyISAM or Memory tables, which
essentially always operate in AUTOCOMMIT mode.
Certain commands, when issued during an open transaction,
cause MySQL to commit the transaction before they execute. These are
typically Data Definition Language (DDL) commands that make significant changes, such as
ALTER TABLE, but LOCK TABLES and some other statements also
have this effect. Check your version’s documentation for the full
list of commands that automatically commit a transaction.
MySQL lets you set the isolation level using the SET TRANSACTION ISOLATION LEVEL command,
which takes effect when the next transaction starts. You can set the
isolation level for the whole server in the configuration file (see
Chapter 6), or just for your
session:
mysql> SET SESSION TRANSACTION ISOLATION LEVEL READ COMMITTED;MySQL recognizes all four ANSI standard isolation levels, and InnoDB supports all of them. Other storage engines have varying support for the different isolation levels.
MySQL doesn’t manage transactions at the server level. Instead, the underlying storage engines implement transactions themselves. This means you can’t reliably mix different engines in a single transaction. MySQL AB is working on adding a higher-level transaction management service to the server, which will make it safe to mix and match transactional tables in a transaction. Until then, be careful.
If you mix transactional and nontransactional tables (for instance, InnoDB and MyISAM tables) in a transaction, the transaction will work properly if all goes well.
However, if a rollback is required, the changes to the nontransactional table can’t be undone. This leaves the database in an inconsistent state from which it may be difficult to recover and renders the entire point of transactions moot. This is why it is really important to pick the right storage engine for each table.
MySQL will not usually warn you or raise errors if you do transactional operations on a nontransactional table. Sometimes rolling back a transaction will generate the warning “Some nontransactional changed tables couldn’t be rolled back,” but most of the time, you’ll have no indication you’re working with nontransactional tables.
InnoDB uses a two-phase locking protocol. It can acquire locks
at any time during a transaction, but it does not release them until
a COMMIT or ROLLBACK. It releases all the locks at the
same time. The locking mechanisms described earlier are all
implicit. InnoDB handles locks automatically,
according to your isolation level.
However, InnoDB also supports explicit locking, which the SQL standard does not mention at all:
SELECT … LOCK IN SHARE MODESELECT … FOR UPDATE
MySQL also supports the LOCK
TABLES and UNLOCK
TABLES commands, which are implemented in the server, not
in the storage engines. These have their uses, but they are not a
substitute for transactions. If you need transactions, use a
transactional storage engine.
We often see applications that have been converted from MyISAM
to InnoDB but are still using LOCK
TABLES. This is no longer necessary because of row-level
locking, and it can cause severe performance problems.
Most of MySQL’s transactional storage engines, such as InnoDB, Falcon, and PBXT, don’t use a simple row-locking mechanism. Instead, they use row-level locking in conjunction with a technique for increasing concurrency known as multiversion concurrency control (MVCC). MVCC is not unique to MySQL: Oracle, PostgreSQL, and some other database systems use it too.
You can think of MVCC as a twist on row-level locking; it avoids the need for locking at all in many cases and can have much lower overhead. Depending on how it is implemented, it can allow nonlocking reads, while locking only the necessary rows during write operations.
MVCC works by keeping a snapshot of the data as it existed at some point in time. This means transactions can see a consistent view of the data, no matter how long they run. It also means different transactions can see different data in the same tables at the same time! If you’ve never experienced this before, it may be confusing, but it will become easier to understand with familiarity.
Each storage engine implements MVCC differently. Some of the variations include optimistic and pessimistic concurrency control. We’ll illustrate one way MVCC works by explaining a simplified version of InnoDB’s behavior.
InnoDB implements MVCC by storing with each row two additional,
hidden values that record when the row was created and when it was
expired (or deleted). Rather than storing the actual times at which
these events occurred, the row stores the system version number at the
time each event occurred. This is a number that increments each time a
transaction begins. Each transaction keeps its own record of the current
system version, as of the time it began. Each query has to check each
row’s version numbers against the transaction’s version. Let’s see how
this applies to particular operations when the transaction isolation
level is set to REPEATABLE
READ:
SELECTInnoDB must examine each row to ensure that it meets two criteria:
InnoDB must find a version of the row that is at least as old as the transaction (i.e., its version must be less than or equal to the transaction’s version). This ensures that either the row existed before the transaction began, or the transaction created or altered the row.
The row’s deletion version must be undefined or greater than the transaction’s version. This ensures that the row wasn’t deleted before the transaction began.
Rows that pass both tests may be returned as the query’s result.
INSERTInnoDB records the current system version number with the new row.
DELETEInnoDB records the current system version number as the row’s deletion ID.
UPDATEInnoDB writes a new copy of the row, using the system version number for the new row’s version. It also writes the system version number as the old row’s deletion version.
The result of all this extra record keeping is that most read queries never acquire locks. They simply read data as fast as they can, making sure to select only rows that meet the criteria. The drawbacks are that the storage engine has to store more data with each row, do more work when examining rows, and handle some additional housekeeping operations.
MVCC works only with the REPEATABLE READ and READ COMMITTED isolation levels. READ
UNCOMMITTED isn’t MVCC-compatible because queries don’t read the row version
that’s appropriate for their transaction version; they read the newest
version, no matter what. SERIALIZABLE
isn’t MVCC-compatible because reads lock every row they return.
Table 1-2 summarizes the various locking models and concurrency levels in MySQL.
This section gives an overview of MySQL’s storage engines. We won’t go into great detail here, because we discuss storage engines and their particular behaviors throughout the book. Even this book, though, isn’t a complete source of documentation; you should read the MySQL manuals for the storage engines you decide to use. MySQL also has forums dedicated to each storage engine, often with links to additional information and interesting ways to use them.
If you just want to compare the engines at a high level, you can skip ahead to Table 1-3.
MySQL stores each database (also called a
schema) as a subdirectory of its data directory in
the underlying filesystem. When you create a table, MySQL stores the
table definition in a .frm file with the same name
as the table. Thus, when you create a table named MyTable, MySQL stores the table definition in
MyTable.frm. Because MySQL uses the filesystem to
store database names and table definitions, case sensitivity depends on
the platform. On a Windows MySQL instance, table and database names are
case insensitive; on Unix-like systems, they are case sensitive. Each
storage engine stores the table’s data and indexes differently, but the
server itself handles the table definition.
To determine what storage engine a particular table uses, use the
SHOW TABLE STATUS command. For
example, to examine the user table in
the mysql database, execute the
following:
mysql> SHOW TABLE STATUS LIKE 'user' \G
*************************** 1. row ***************************
Name: user
Engine: MyISAM
Row_format: Dynamic
Rows: 6
Avg_row_length: 59
Data_length: 356
Max_data_length: 4294967295
Index_length: 2048
Data_free: 0
Auto_increment: NULL
Create_time: 2002-01-24 18:07:17
Update_time: 2002-01-24 21:56:29
Check_time: NULL
Collation: utf8_bin
Checksum: NULL
Create_options:
Comment: Users and global privileges
1 row in set (0.00 sec)The output shows that this is a MyISAM table. You might also notice a lot of other information and statistics in the output. Let’s briefly look at what each line means:
NameThe table’s name.
EngineThe table’s storage engine. In old versions of MySQL, this column was named
Type, notEngine.Row_formatThe row format. For a MyISAM table, this can be
Dynamic, Fixed, orCompressed. Dynamic rows vary in length because they contain variable-length fields such asVARCHARorBLOB. Fixed rows, which are always the same size, are made up of fields that don’t vary in length, such asCHARandINTEGER. Compressed rows exist only in compressed tables; see “Compressed MyISAM tables” on Compressed MyISAM tables.RowsThe number of rows in the table. For nontransactional tables, this number is always accurate. For transactional tables, it is usually an estimate.
Avg_row_lengthHow many bytes the average row contains.
Data_lengthHow much data (in bytes) the entire table contains.
Max_data_lengthThe maximum amount of data this table can hold. See “Storage” on The MyISAM Engine for more details.
Index_lengthHow much disk space the index data consumes.
Data_freeFor a MyISAM table, the amount of space that is allocated but currently unused. This space holds previously deleted rows and can be reclaimed by future
INSERTstatements.Auto_incrementThe next
AUTO_INCREMENTvalue.Create_timeWhen the table was first created.
Update_timeWhen data in the table last changed.
Check_timeWhen the table was last checked using
CHECK TABLEor myisamchk.CollationThe default character set and collation for character columns in this table. See “Character Sets and Collations” on Character Sets and Collations for more on these features.
ChecksumA live checksum of the entire table’s contents if enabled.
Create_optionsAny other options that were specified when the table was created.
CommentThis field contains a variety of extra information. For a MyISAM table, it contains the comments, if any, that were set when the table was created. If the table uses the InnoDB storage engine, the amount of free space in the InnoDB tablespace appears here. If the table is a view, the comment contains the text “VIEW.”
As MySQL’s default storage engine, MyISAM provides a good compromise between performance and useful features, such as full-text indexing, compression, and spatial (GIS) functions. MyISAM doesn’t support transactions or row-level locks.
MyISAM typically stores each table in two files: a data file and an index file. The two files bear .MYD and .MYI extensions, respectively. The MyISAM format is platform-neutral, meaning you can copy the data and index files from an Intel-based server to a PowerPC or Sun SPARC without any trouble.
MyISAM tables can contain either dynamic or static (fixed-length) rows. MySQL decides which format to use based on the table definition. The number of rows a MyISAM table can hold is limited primarily by the available disk space on your database server and the largest file your operating system will let you create.
MyISAM tables created in MySQL 5.0 with variable-length rows
are configured by default to handle 256 TB of data, using 6-byte
pointers to the data records. Earlier MySQL versions defaulted to
4-byte pointers, for up to 4 GB of data. All MySQL versions can
handle a pointer size of up to 8 bytes. To change the pointer size
on a MyISAM table (either up or down), you must specify values for
the MAX_ROWS and AVG_ROW_LENGTH options that represent
ballpark figures for the amount of space you need:
CREATE TABLE mytable ( a INTEGER NOT NULL PRIMARY KEY, b CHAR(18) NOT NULL ) MAX_ROWS = 1000000000 AVG_ROW_LENGTH = 32;
In this example, we’ve told MySQL to be prepared to store at least 32 GB of data in the table. To find out what MySQL decided to do, simply ask for the table status:
mysql> SHOW TABLE STATUS LIKE 'mytable' \G
*************************** 1. row ***************************
Name: mytable
Engine: MyISAM
Row_format: Fixed
Rows: 0
Avg_row_length: 0
Data_length: 0
Max_data_length: 98784247807
Index_length: 1024
Data_free: 0
Auto_increment: NULL
Create_time: 2002-02-24 17:36:57
Update_time: 2002-02-24 17:36:57
Check_time: NULL
Create_options: max_rows=1000000000 avg_row_length=32
Comment:
1 row in set (0.05 sec)As you can see, MySQL remembers the create options exactly as
specified. And it chose a representation capable of holding 91 GB of
data! You can change the pointer size later with the ALTER TABLE statement, but that will cause
the entire table and all of its indexes to be rewritten, which may
take a long time.
As one of the oldest storage engines included in MySQL, MyISAM has many features that have been developed over years of use to fill niche needs:
- Locking and concurrency
MyISAM locks entire tables, not rows. Readers obtain shared (read) locks on all tables they need to read. Writers obtain exclusive (write) locks. However, you can insert new rows into the table while select queries are running against it (concurrent inserts). This is a very important and useful feature.
- Automatic repair
MySQL supports automatic checking and repairing of MyISAM tables. See “MyISAM I/O Tuning” on Tuning MySQL’s I/O Behavior for more information.
- Manual repair
You can use the
CHECK TABLE mytableandREPAIR TABLE mytablecommands to check a table for errors and repair them. You can also use the myisamchk command-line tool to check and repair tables when the server is offline.- Index features
You can create indexes on the first 500 characters of
BLOBandTEXTcolumns in MyISAM tables. MyISAM supports full-text indexes, which index individual words for complex search operations. For more information on indexing, see Chapter 3.- Delayed key writes
MyISAM tables marked with the
DELAY_KEY_WRITEcreate option don’t write changed index data to disk at the end of a query. Instead, MyISAM buffers the changes in the in-memory key buffer. It flushes index blocks to disk when it prunes the buffer or closes the table. This can boost performance on heavily used tables that change frequently. However, after a server or system crash, the indexes will definitely be corrupted and will need repair. You should handle this with a script that runs myisamchk before restarting the server, or by using the automatic recovery options. (Even if you don’t useDELAY_KEY_WRITE, these safeguards can still be an excellent idea.) You can configure delayed key writes globally, as well as for individual tables.
Some tables—for example, in CD-ROM- or DVD-ROM-based applications and some embedded environments—never change once they’re created and filled with data. These might be well suited to compressed MyISAM tables.
You can compress (or “pack”) tables with the myisampack utility. You can’t modify compressed tables (although you can uncompress, modify, and recompress tables if you need to), but they generally use less space on disk. As a result, they offer faster performance, because their smaller size requires fewer disk seeks to find records. Compressed MyISAM tables can have indexes, but they’re read-only.
The overhead of decompressing the data to read it is insignificant for most applications on modern hardware, where the real gain is in reducing disk I/O. The rows are compressed individually, so MySQL doesn’t need to unpack an entire table (or even a page) just to fetch a single row.
The Merge engine is a variation of MyISAM. A Merge table is the combination of several identical MyISAM tables into one virtual table. This is particularly useful when you use MySQL in logging and data warehousing applications. See “Merge Tables and Partitioning” on Merge Tables and Partitioning for a detailed discussion of Merge tables.
InnoDB was designed for transaction processing—specifically, processing of many short-lived transactions that usually complete rather than being rolled back. It remains the most popular storage engine for transactional storage. Its performance and automatic crash recovery make it popular for nontransactional storage needs, too.
InnoDB stores its data in a series of one or more data files that are collectively known as a tablespace. A tablespace is essentially a black box that InnoDB manages all by itself. In MySQL 4.1 and newer versions, InnoDB can store each table’s data and indexes in separate files. InnoDB can also use raw disk partitions for building its tablespace. See “The InnoDB tablespace” on The InnoDB tablespace for more information.
InnoDB uses MVCC to achieve high concurrency, and it implements all four SQL standard
isolation levels. It defaults to the REPEATABLE READ isolation level, and it has
a next-key locking strategy that prevents phantom
reads in this isolation level: rather than locking only the rows you’ve touched in a query, InnoDB
locks gaps in the index structure as well, preventing phantoms from
being inserted.
InnoDB tables are built on a clustered index, which we will cover in detail in Chapter 3. InnoDB’s index structures are very different from those of most other MySQL storage engines. As a result, it provides very fast primary key lookups. However, secondary indexes (indexes that aren’t the primary key) contain the primary key columns, so if your primary key is large, other indexes will also be large. You should strive for a small primary key if you’ll have many indexes on a table. InnoDB doesn’t compress its indexes.
At the time of this writing, InnoDB can’t build indexes by sorting, which MyISAM can do. Thus, InnoDB loads data and creates indexes more slowly than MyISAM. Any operation that changes an InnoDB table’s structure will rebuild the entire table, including all the indexes.
InnoDB was designed when most servers had slow disks, a single CPU, and limited memory. Today, as multicore servers with huge amounts of memory and fast disks are becoming less expensive, InnoDB is experiencing some scalability issues.
InnoDB’s developers are addressing these issues, but at the time of this writing, several of them remain problematic. See “InnoDB Concurrency Tuning” on InnoDB Concurrency Tuning for more information about achieving high concurrency with InnoDB.
Besides its high-concurrency capabilities, InnoDB’s next most popular feature is foreign key constraints, which the MySQL server itself doesn’t yet provide. InnoDB also provides extremely fast lookups for queries that use a primary key.
InnoDB has a variety of internal optimizations. These include predictive read-ahead for prefetching data from disk, an adaptive hash index that automatically builds hash indexes in memory for very fast lookups, and an insert buffer to speed inserts. We cover these extensively later in this book.
InnoDB’s behavior is very intricate, and we highly recommend reading the “InnoDB Transaction Model and Locking” section of the MySQL manual if you’re using InnoDB. There are many surprises and exceptions you should be aware of before building an application with InnoDB.
Memory tables (formerly called HEAP tables) are useful when you need fast
access to data that either never changes or doesn’t need to persist
after a restart. Memory tables are generally about an order of
magnitude faster than MyISAM tables. All of their data is stored in
memory, so queries don’t have to wait for disk I/O. The table
structure of a Memory table persists across a server restart, but no
data survives.
Here are some good uses for Memory tables:
For “lookup” or “mapping” tables, such as a table that maps postal codes to state names
For caching the results of periodically aggregated data
For intermediate results when analyzing data
Memory tables support HASH
indexes, which are very fast for lookup queries. See “Hash indexes” on
Hash indexes for more information on HASH indexes.
Although Memory tables are very fast, they often don’t work well
as a general-purpose replacement for disk-based tables. They use
table-level locking, which gives low write concurrency, and they do
not support TEXT or BLOB column types. They also support only
fixed-size rows, so they really store VARCHARs as CHARs, which can waste memory.
MySQL uses the Memory engine internally while processing queries
that require a temporary table to hold intermediate results. If the
intermediate result becomes too large for a Memory table, or has
TEXT or BLOB columns, MySQL will convert it to a
MyISAM table on disk. We say more about this in later chapters.
Tip
People often confuse Memory tables with temporary tables, which are ephemeral tables
created with CREATE TEMPORARY
TABLE. Temporary tables can use any storage engine; they are not the same thing as tables
that use the Memory storage engine. Temporary tables are visible
only to a single connection and disappear entirely when the
connection closes.
The Archive engine supports only INSERT and SELECT queries, and it does not support
indexes until MySQL 5.1. It causes much less disk I/O than MyISAM,
because it buffers data writes and compresses each row with
zlib as it’s inserted. Also, each SELECT query requires a full table scan.
Archive tables are thus ideal for logging and data acquisition, where
analysis tends to scan an entire table, or where you want fast
INSERT queries on a replication
master. Replication slaves can use a different storage engine for the
same table, which means the table on the slave can have indexes for
faster performance on analysis. (See Chapter 8
for more about replication.)
Archive supports row-level locking and a special buffer system
for high-concurrency inserts. It gives consistent reads by stopping a
SELECT after it has retrieved the
number of rows that existed in the table when the query began. It also
makes bulk inserts invisible until they’re complete. These features
emulate some aspects of transactional and MVCC behaviors, but Archive
is not a transactional storage engine. It is simply a storage engine
that’s optimized for high-speed inserting and compressed
storage.
The CSV engine can treat comma-separated values (CSV) files as tables, but it does not support indexes on them. This engine lets you copy files in and out of the database while the server is running. If you export a CSV file from a spreadsheet and save it in the MySQL server’s data directory, the server can read it immediately. Similarly, if you write data to a CSV table, an external program can read it right away. CSV tables are especially useful as a data interchange format and for certain kinds of logging.
The Federated engine does not store data locally. Each Federated table refers to a table on a remote MySQL server, so it actually connects to a remote server for all operations. It is sometimes used to enable “hacks” such as tricks with replication.
There are many oddities and limitations in the current
implementation of this engine. Because of the way the Federated engine
works, we think it is most useful for single-row lookups by primary
key, or for INSERT queries you want
to affect a remote server. It does not perform well for aggregate
queries, joins, or other basic operations.
The Blackhole engine has no storage mechanism at all. It
discards every INSERT instead of
storing it. However, the server writes queries against Blackhole
tables to its logs as usual, so they can be replicated to slaves or
simply kept in the log. That makes the Blackhole engine useful for
fancy replication setups and audit logging.
MySQL AB acquired the NDB Cluster engine from Sony Ericsson in 2003. It was originally designed for high speed (real-time performance requirements), with redundancy and load-balancing capabilities. Although it logged to disk, it kept all its data in memory and was optimized for primary key lookups. MySQL has since added other indexing methods and many optimizations, and MySQL 5.1 allows some columns to be stored on disk.
The NDB architecture is unique: an NDB cluster is completely unlike, for example, an Oracle cluster. NDB’s infrastructure is based on a shared-nothing concept. There is no storage area network or other big centralized storage solution, which some other types of clusters rely on. An NDB database consists of data nodes, management nodes, and SQL nodes (MySQL instances). Each data node holds a segment (“fragment”) of the cluster’s data. The fragments are duplicated, so the system has multiple copies of the same data on different nodes. One physical server is usually dedicated to each node for redundancy and high availability. In this sense, NDB is similar to RAID at the server level.
The management nodes are used to retrieve the centralized configuration, and for monitoring and control of the cluster nodes. All data nodes communicate with each other, and all MySQL servers connect to all data nodes. Low network latency is critically important for NDB Cluster.
A word of warning: NDB Cluster is very “cool” technology and definitely worth some exploration to satisfy your curiosity, but many technical people tend to look for excuses to use it and attempt to apply it to needs for which it’s not suitable. In our experience, even after studying it carefully, many people don’t really learn what this engine is useful for and how it works until they’ve installed it and used it for a while. This commonly results in much wasted time, because it is simply not designed as a general-purpose storage engine.
One common shock is that NDB currently performs joins at the MySQL server level, not in the storage engine layer. Because all data for NDB must be retrieved over the network, complex joins are extremely slow. On the other hand, single-table lookups can be very fast, because multiple data nodes each provide part of the result. This is just one of many aspects you’ll have to consider and understand thoroughly when looking at NDB Cluster for a particular application.
NDB Cluster is so large and complex that we won’t discuss it further in this book. You should seek out a book dedicated to the topic if you are interested in it. We will say, however, that it’s generally not what you think it is, and for most traditional applications, it is not the answer.
Jim Starkey, a database pioneer whose earlier inventions
include Interbase, MVCC, and the BLOB column type, designed the Falcon
engine. MySQL AB acquired the Falcon technology in 2006, and Jim
currently works for MySQL AB.
Falcon is designed for today’s hardware—specifically, for servers with multiple 64-bit processors and plenty of memory—but it can also operate in more modest environments. Falcon uses MVCC and tries to keep running transactions entirely in memory. This makes rollbacks and recovery operations extremely fast.
Falcon is unfinished at the time of this writing (for example, it doesn’t yet synchronize its commits with the binary log), so we can’t write about it with much authority. Even the initial benchmarks we’ve done with it will probably be outdated when it’s ready for general use. It appears to have good potential for many online applications, but we’ll know more about it as time passes.
The solidDB engine, developed by Solid Information Technology (http://www.soliddb.com), is a transactional engine that uses MVCC. It supports both pessimistic and optimistic concurrency control, which no other engine currently does. solidDB for MySQL includes full foreign key support. It is similar to InnoDB in many ways, such as its use of clustered indexes. solidDB for MySQL includes an online backup capability at no charge.
The solidDB for MySQL product is a complete package that consists of the solidDB storage engine, the MyISAM storage engine, and MySQL server. The “glue” between the solidDB storage engine and the MySQL server was introduced in late 2006. However, the underlying technology and code have matured over the company’s 15-year history. Solid certifies and supports the entire product. It is licensed under the GPL and offered commercially under a dual-licensing model that is identical to the MySQL server’s.
The PBXT engine, developed by Paul McCullagh of SNAP Innovation GmbH in Hamburg, Germany (http://www.primebase.com), is a transactional storage engine with a unique design. One of its distinguishing characteristics is how it uses its transaction logs and data files to avoid write-ahead logging, which reduces much of the overhead of transaction commits. This architecture gives PBXT the potential to deal with very high write concurrency, and tests have already shown that it can be faster than InnoDB for certain operations. PBXT uses MVCC and supports foreign key constraints, but it does not use clustered indexes.
PBXT is a fairly new engine, and it will need to prove itself further in production environments. For example, its implementation of truly durable transactions was completed only recently, while we were writing this book.
As an extension to PBXT, SNAP Innovation is working on a scalable "blob streaming” infrastructure (http://www.blobstreaming.org). It is designed to store and retrieve large chunks of binary data efficiently.
Maria is a new storage engine being developed by some of MySQL’s top engineers, including Michael Widenius, who created MySQL. The initial 1.0 release includes only some of its planned features.
The goal is to use Maria as a replacement for MyISAM, which is currently MySQL’s default storage engine, and which the server uses internally for tasks such as privilege tables and temporary tables created while executing queries. Here are some highlights from the roadmap:
The option of either transactional or nontransactional storage, on a per-table basis
Crash recovery, even when a table is running in nontransactional mode
Row-level locking and MVCC
Better
BLOBhandling
Various third parties offer other (sometimes proprietary) engines, and there are a myriad of special-purpose and experimental engines out there (for example, an engine for querying web services). Some of these engines are developed informally, perhaps by just one or two engineers. This is because it’s relatively easy to create a storage engine for MySQL. However, most such engines aren’t widely publicized, in part because of their limited applicability. We’ll leave you to explore these offerings on your own.
When designing MySQL-based applications, you should decide which storage engine to use for storing your data. If you don’t think about this during the design phase, you will likely face complications later in the process. You might find that the default engine doesn’t provide a feature you need, such as transactions, or maybe the mix of read and write queries your application generates will require more granular locking than MyISAM’s table locks.
Because you can choose storage engines on a table-by-table basis, you’ll need a clear idea of how each table will be used and the data it will store. It also helps to have a good understanding of the application as a whole and its potential for growth. Armed with this information, you can begin to make good choices about which storage engines can do the job.
Although many factors can affect your decision about which storage engine(s) to use, it usually boils down to a few primary considerations. Here are the main elements you should take into account:
- Transactions
If your application requires transactions, InnoDB is the most stable, well-integrated, proven choice at the time of this writing. However, we expect to see the up-and-coming transactional engines become strong contenders as time passes.
MyISAM is a good choice if a task doesn’t require transactions and issues primarily either
SELECTorINSERTqueries. Sometimes specific components of an application (such as logging) fall into this category.- Concurrency
How best to satisfy your concurrency requirements depends on your workload. If you just need to insert and read concurrently, believe it or not, MyISAM is a fine choice! If you need to allow a mixture of operations to run concurrently without interfering with each other, one of the engines with row-level locking should work well.
- Backups
The need to perform regular backups may also influence your table choices. If your server can be shut down at regular intervals for backups, the storage engines are equally easy to deal with. However, if you need to perform online backups in one form or another, the choices become less clear. Chapter 11 deals with this topic in more detail.
Also bear in mind that using multiple storage engines increases the complexity of backups and server tuning.
- Crash recovery
If you have a lot of data, you should seriously consider how long it will take to recover from a crash. MyISAM tables generally become corrupt more easily and take much longer to recover than InnoDB tables, for example. In fact, this is one of the most important reasons why a lot of people use InnoDB when they don’t need transactions.
- Special features
Finally, you sometimes find that an application relies on particular features or optimizations that only some of MySQL’s storage engines provide. For example, a lot of applications rely on clustered index optimizations. At the moment, that limits you to InnoDB and solidDB. On the other hand, only MyISAM supports full-text search inside MySQL. If a storage engine meets one or more critical requirements, but not others, you need to either compromise or find a clever design solution. You can often get what you need from a storage engine that seemingly doesn’t support your requirements.
You don’t need to decide right now. There’s a lot of material on each storage engine’s strengths and weaknesses in the rest of the book, and lots of architecture and design tips as well. In general, there are probably more options than you realize yet, and it might help to come back to this question after reading more.
These issues may seem rather abstract without some sort of real-world context, so let’s consider some common database applications. We’ll look at a variety of tables and determine which engine best matches with each table’s needs. We give a summary of the options in the next section.
Suppose you want to use MySQL to log a record of every telephone call from a central telephone switch in real time. Or maybe you’ve installed mod_log_sql for Apache, so you can log all visits to your web site directly in a table. In such an application, speed is probably the most important goal; you don’t want the database to be the bottleneck. The MyISAM and Archive storage engines would work very well because they have very low overhead and can insert thousands of records per second. The PBXT storage engine is also likely to be particularly suitable for logging purposes.
Things will get interesting, however, if you decide it’s time to start running reports to summarize the data you’ve logged. Depending on the queries you use, there’s a good chance that gathering data for the report will significantly slow the process of inserting records. What can you do?
One solution is to use MySQL’s built-in replication feature to clone the data onto a second (slave) server, and then run your time- and CPU-intensive queries against the data on the slave. This leaves the master free to insert records and lets you run any query you want on the slave without worrying about how it might affect the real-time logging.
You can also run queries at times of low load, but don’t rely on this strategy continuing to work as your application grows.
Another option is to use a Merge table. Rather than always
logging to the same table, adjust the application to log to a table
that contains the year and name or number of the month in its name,
such as web_logs_2008_01 or
web_logs_2008_jan. Then define a
Merge table that contains the data you’d like to summarize and use
it in your queries. If you need to summarize data daily or weekly,
the same strategy works; you just need to create tables with more
specific names, such as web_logs_2008_01_01. While you’re busy
running queries against tables that are no longer being written to,
your application can log records to its current table
uninterrupted.
Tables that contain data used to construct a catalog or listing of some sort (jobs, auctions, real estate, etc.) are usually read from far more often than they are written to. This makes them good candidates for MyISAM—if you don’t mind what happens when MyISAM crashes. Don’t underestimate how important this is; a lot of users don’t really understand how risky it is to use a storage engine that doesn’t even try very hard to get their data written to disk.
Tip
It’s an excellent idea to run a realistic load simulation on a test server and then literally pull the power plug. The firsthand experience of recovering from a crash is priceless. It saves nasty surprises later.
Don’t just believe the common “MyISAM is faster than InnoDB” folk wisdom. It is not categorically true. We can name dozens of situations where InnoDB leaves MyISAM in the dust, especially for applications where clustered indexes are useful or where the data fits in memory. As you read the rest of this book, you’ll get a sense of which factors influence a storage engine’s performance (data size, number of I/O operations required, primary keys versus secondary indexes, etc.), and which of them matter to your application.
When you deal with any sort of order processing, transactions are all but required. Half-completed orders aren’t going to endear customers to your service. Another important consideration is whether the engine needs to support foreign key constraints. At the time of this writing, InnoDB is likely to be your best bet for order-processing applications, though any of the transactional storage engines is a candidate.
If you’re collecting stock quotes for your own analysis, MyISAM works great, with the usual caveats. However, if you’re running a high-traffic web service that has a real-time quote feed and thousands of users, a query should never have to wait. Many clients could be trying to read and write to the table simultaneously, so row-level locking or a design that minimizes updates is the way to go.
Threaded discussions are an interesting problem for MySQL users. There are hundreds of freely available PHP and Perl-based systems that provide threaded discussions. Many of them aren’t written with database efficiency in mind, so they tend to run a lot of queries for each request they serve. Some were written to be database independent, so their queries do not take advantage of the features of any one database system. They also tend to update counters and compile usage statistics about the various discussions. Many of the systems also use a few monolithic tables to store all their data. As a result, a few central tables become the focus of heavy read and write activity, and the locks required to enforce consistency become a substantial source of contention.
Despite their design shortcomings, most of the systems work well for small and medium loads. However, if a web site grows large enough and generates significant traffic, it may become very slow. The obvious solution is to switch to a different storage engine that can handle the heavy read/write volume, but users who attempt this are sometimes surprised to find that the systems run even more slowly than they did before!
What these users don’t realize is that the system is using a particular query, normally something like this:
mysql> SELECT COUNT(*) FROM table;The problem is that not all engines can run that query quickly: MyISAM can, but other engines may not. There are similar examples for every engine. Chapter 2 will help you keep such a situation from catching you by surprise and show you how to find and fix the problems if it does.
If you ever need to distribute a CD-ROM- or DVD-ROM-based application that uses MySQL data files, consider using MyISAM or compressed MyISAM tables, which can easily be isolated and copied to other media. Compressed MyISAM tables use far less space than uncompressed ones, but they are read-only. This can be problematic in certain applications, but because the data is going to be on read-only media anyway, there’s little reason not to use compressed tables for this particular task.
Table 1-3 summarizes the transaction- and locking-related traits of MySQL’s most popular storage engines. The MySQL version column shows the minimum MySQL version you’ll need to use the engine, though for some engines and MySQL versions you may have to compile your own server. The word “All” in this column indicates all versions since MySQL 3.23.
Table 1-3. MySQL storage engine summary
Storage engine | MySQL version | Transactions | Lock granularity | Key applications | Counter-indications |
|---|---|---|---|---|---|
All | No | Table with concurrent inserts |
| Mixed read/write workload | |
All | No | Table with concurrent inserts | Segmented archiving, data warehousing | Many global lookups | |
All | No | Table | Intermediate calculations, static lookup data | Large datasets, persistent storage | |
All | Yes | Row-level with MVCC | Transactional processing | None | |
6.0 | Yes | Row-level with MVCC | Transactional processing | None | |
4.1 | No | Row-level | Logging, aggregate analysis | Random access needs, updates, deletes | |
4.1 | No | Table | Logging, bulk loading of external data | Random access needs, indexing | |
4.1 | N/A | N/A | Logged or replicated archiving | Any but the intended use | |
5.0 | N/A | N/A | Distributed data sources | Any but the intended use | |
5.0 | Yes | Row-level | High availability | Most typical uses | |
5.0 | Yes | Row-level with MVCC | Transactional processing, logging | Need for clustered indexes | |
5.0 | Yes | Row-level with MVCC | Transactional processing | None | |
6.x | Yes | Row-level with MVCC | MyISAM replacement | None |
There are several ways to convert a table from one storage engine to another, each with advantages and disadvantages. In the following sections, we cover three of the most common ways.
The easiest way to move a table from one engine to another is
with an ALTER TABLE statement.
The following command converts mytable to Falcon:
mysql> ALTER TABLE mytable ENGINE = Falcon;This syntax works for all storage engines, but there’s a catch: it can take a lot of time. MySQL will perform a row-by-row copy of your old table into a new table. During that time, you’ll probably be using all of the server’s disk I/O capacity, and the original table will be read-locked while the conversion runs. So, take care before trying this technique on a busy table. Instead, you can use one of the methods discussed next, which involve making a copy of the table first.
When you convert from one storage engine to another, any storage engine-specific features are lost. For example, if you convert an InnoDB table to MyISAM and back again, you will lose any foreign keys originally defined on the InnoDB table.
To gain more control over the conversion process, you might
choose to first dump the table to a text file using the
mysqldump utility. Once you’ve dumped the
table, you can simply edit the dump file to adjust the CREATE TABLE statement it contains. Be
sure to change the table name as well as its type, because you can’t
have two tables with the same name in the same database even if they
are of different types—and mysqldump defaults
to writing a DROP TABLE command
before the CREATE TABLE, so you
might lose your data if you are not careful!
See Chapter 11 for more advice on dumping and reloading data efficiently.
The third conversion technique is a compromise between the
first mechanism’s speed and the safety of the second. Rather than
dumping the entire table or converting it all at once, create the new table and
use MySQL’s INSERT … SELECT
syntax to populate it, as follows:
mysql>CREATE TABLE innodb_table LIKE myisam_table;mysql>ALTER TABLE innodb_table ENGINE=InnoDB;mysql>INSERT INTO innodb_table SELECT * FROM myisam_table;
That works well if you don’t have much data, but if you do,
it’s often more efficient to populate the table incrementally,
committing the transaction between each chunk so the undo logs don’t
grow huge. Assuming that id is
the primary key, run this query repeatedly (using larger values of
x and y each time) until you’ve copied all the
data to the new table:
mysql>START TRANSACTION;mysql>INSERT INTO innodb_table SELECT * FROM myisam_table->WHERE id BETWEEN x AND y;mysql>COMMIT;
After doing so, you’ll be left with the original table, which you can drop when you’re done with it, and the new table, which is now fully populated. Be careful to lock the original table if needed to prevent getting an inconsistent copy of the data!
Get High Performance MySQL, 2nd Edition now with the O’Reilly learning platform.
O’Reilly members experience books, live events, courses curated by job role, and more from O’Reilly and nearly 200 top publishers.