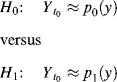Hyperspectral Data Processing: Algorithm Design and Analysis

3.2 Neyman–Pearson Detection Problem Formulation

In Section 2.2.1 a binary hypothesis testing problem (2.1) is used to formulate the pure-sample target detection as two hypotheses, H₀ and H₁, which represent the absence and presence of a signal source in an observed sample r, respectively. This section places its main focus on a particular type of detection problem when there is no prior knowledge of the two hypotheses and cost functions. It is generally called the Neyman–Pearson detection problem cast by (2.9–2.11).

More specifically, assume that the observation process is described by a random process Y_t. When this process is observed at a particular time instant t = t₀, it is referred to as an observation y which can be described by a random variable . If the probability distribution of is further assumed to be P(y) with its probability density function given by p(y), the binary hypothesis testing problem (2.1) can be described by

(3.1)

where the hypotheses H₀ and H₁ can be observed from the variable whose probability distributions are derived from p(y) under each hypothesis, denoted ...