Hyperspectral Data Processing: Algorithm Design and Analysis

14.3 Weighted Least-Squares Abundance-Constrained LSMA

It should be noted that the LSE specified by (14.1) does not include a weighting matrix to account for significance of bands in signatures used to form the M, in which case the identity matrix I is used in (14.4)–(14.6). However, this is not necessarily an optimal way to impose LSE since it weights LSE caused by each band equally significant. If a weighting matrix A is included in (14.2) to account for LSEs resulting from different bands (i.e., replacing I in (14.1) with A), then an A-weighted LSE problem is to find a solution that solves

(14.7)

Suppose that A is a positive-definite and symmetric matrix; we can use that is, the square-root form of A to whiten the LSE in (14.7) as follows:

(14.8)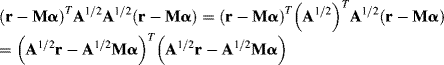

Using a linear transformation defined by

(14.9)

an A-whitened LSE can be obtained by

(14.10)

which is reduced to minimization of (14.2), except that both the image pixel vector and the matrix have been whitened by the weighting matrix ...