Hyperspectral Data Processing: Algorithm Design and Analysis

31.4 Feature Dimensionality Expansion by Nonlinear Kernels

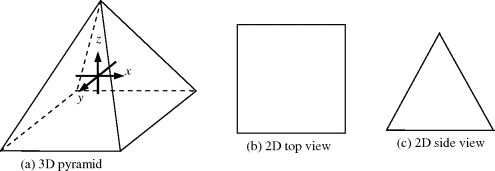
Unlike BDE, which expands band dimensionality to resolve the issue in use of an insufficient number of spectral bands, FDE makes a rather different attempt by expanding features used by classification to a high dimensional feature space via a nonlinear kernel so that the linear nonseparability issue arising in the original data space can be resolved in a new feature space. Its idea can be briefly illustrated by the following example. Assume that a three-dimensional (3D) pyramid shown in Figure 31.5(a) is viewed in a two-dimensional space. It must require two views, a 2D top view shown in Figure 31.5(b) and a 2D side view shown in Figure 31.5(c) to completely envision what a pyramid looks like in a 3D space.

Using the pyramid in Figure 31.4(a) as an example, solving a linear nonseparable problem in an original data space is similar to viewing a pyramid in a two-dimensional data space, which requires two different views, top and side views, to capture its shape, which can only be visualized in a three-dimensional space. This is equivalent to expanding two top and side views to a single view of a pyramid in a three-dimesnional space shown in Figure 31.4(a), which becomes linearly separable problem.

Figure 31.4 A three-dimensional pyramid can be viewed by jointly 2 two-dimensional top and side views.

Two kernel-based approaches ...