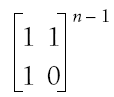Intel Threading Building Blocks

Example Program for Fibonacci Numbers

This section uses the computation of the Fibonacci numbers as an example to illustrate the direct use of the Intel Threading Building Blocks task scheduler. A Fibonacci number in the Fibonacci series F is defined as the sum of the previous two terms:

Fn = Fn − 1 + Fn − 2

Therefore, the seventh Fibonacci number of the series beginning with F₀ = 0, F₁ = 1 is 8 (F₆ = 8). This example uses an inefficient method to compute Fibonacci numbers, but it demonstrates the basics of a task library using a simple recursive pattern.

To get scalable speedup out of task-based programming, you need to specify a lot of tasks. This is typically done in Threading Building Blocks with a recursive task pattern.

Example 9-1 shows a traditional, serial solution using recursion.

ora: Efficient Fibonacci Number Calculation

Fibonacci number computation is a classic computer science example for showing recursion, but it is also a classic example in which a simple algorithm is inefficient. A more efficient method would be to compute:

and take the upper-left element. The exponentiation over the matrix can be done quickly via repeated squaring. But we’ll go ahead in this section and use the classic recursion example for teaching purposes.

Example 9-1. Fibonacci serial version

long SerialFib( long n ) {
    if( n<2 )
        return n;
    else
        return SerialFib(n-1)+SerialFib(n-2);
}

The top-level code ...