Introducing Geographic Information Systems with ArcGIS: A Workbook Approach to Learning GIS, 3rd Edition

Proving Pythagoras Right

If you’re like most people, particularly those who are primarily spatially minded, you (vaguely) know the law of Pythagoras, but probably not why it is true. So, for those who are interested, here is a proof—one that will appeal to those interested in graphical, rather than strictly algebraic, matters. (If you just want to take my word for the validity of the law, you may skip the remainder of this discussion.)

Draw a square on a piece of paper. Draw a smaller square within the first, rotated so that its corners touch the sides of the first square. Call the line segment running south from the northwest corner of the big square to the point where the smaller square touches it “a.” Call the segment running north from the southwest corner of the big square to the touching point “b.” Label all of the line segments around the big square with “a” or “b,” as appropriate. Label each of the sides of the smaller square “c.” See Figure 8-13.

FIGURE 8-13 Re-proving the Pythagorean theorem

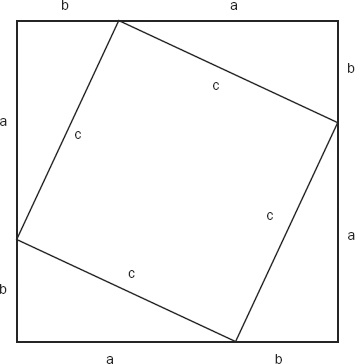
Now compute the areas. The area of each of the four triangles is ½ab. So the total area of all four triangles is 2ab. The area of the smaller square is, of course, c squared. What is the area of the larger square? The length of each side is a + b, so the area of the square is (a + b) times (a + b). When you multiply it out, that’s:

a2 + 2ab + b2

Note now, by looking at the figure, ...