Introducing Geographic Information Systems with ArcGIS: A Workbook Approach to Learning GIS, 3rd Edition

Determining Where Something Is: Coordinate Systems

Cartesian Coordinate Systems

A coordinate system is a way of determining where points lie in space. We are interested in two-dimensional (2-D) space and three-dimensional (3-D) space. In general, it takes two numbers to assign a position to a 2-D space and three numbers in 3-D space.

Coordinates may be thought of as providing an index to the locations of points in space, and hence to the features that these points define.

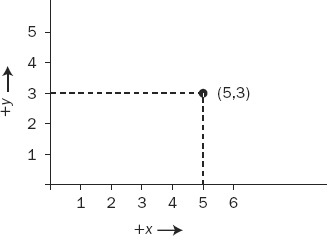
To make a 2-D Cartesian5 coordinate system, draw two axes (lines) that cross at right angles on a piece of paper. The point at which they cross is called the “origin.” The sheet of paper is the x–y plane. Arrange the page on a horizontal table in front of you so that one line points left–right and the other toward and away from you. The part of the line from the origin to your right is called the positive x-axis. The line from the origin away from you is called the positive y-axis. Mark each axis in equal linear units (centimeters, say) starting at the origin, as shown in Figure 1-5. Now, a pair of numbers serves as a reference to any point on the plane. The position x = 5 and y = 3 [shorthand: (5,3)] is shown.

FIGURE 1-5 2-D Cartesian coordinate system

You can create a 3-D Cartesian coordinate system from the 2-D version: Imagine a vertical line passing through the origin; call it the z-axis; the positive direction ...