Introduction to Linear Regression Analysis, 5th Edition

APPENDIX C

SUPPLEMENTAL TECHNICAL MATERIAL

C.1 Background on Basic Test Statistics

C.2 Background from the Theory of linear Models

C.3 Important Results on SS_R and SS_Res

C.4 Gauss-Markov Theorem, Var(ε) = σ²I

C.5 Computational Aspects of Multiple Regression

C.6 Result on the Inverse of a Matrix

C.7 Development of the PRESS Statistic

C.8 Development of S²_(i)

C.9 Outlier Test Based on R-Student

C.10 Independence of Residuals and Fitted Values

C.11 Gauss-Markov Theorem, Var(ε) = V

C.12 Bias in MS_Res When the Model Is Underspecified

C.13 Computation of Influence Diagnostics

C.14 Generalized Linear Models

C.1 BACKGROUND ON BASIC TEST STATISTICS

We indicate that Y is a random variable that follows a normal distribution with mean μ and variance σ² by

C.1.1 Central Distributions

1. Let Y₁, Y₂, …, Y_n be independent normally distributed random variables with E(Y_i) = μ_i and Var(Y_i) = σ²_i. Let a₁, a₂, …, a_n be known constants. If we define the linear combination of the Y_i's by

   

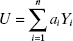
   then

   

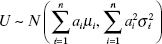
   The key point is that linear combinations of normally distributed random variables also follow normal distributions.

2. If Y ~ N(μ, σ²), then

   Z is called the standard normal random variable.

3. Let Z = (Y – μ)/σ. If Y