Investment Theory and Risk Management, + Website

Pricing European Call Options

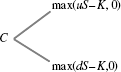
Let's use the idea of a replicating portfolio to derive the value of a call option. We'll begin with a single period problem depicted in Figure 16.5. Think of a stock whose spot price S can go up at the end of one period by a factor u to the level uS or can go down by a factor d to dS. I will derive the parameters u and d in Chapter 17. Moreover, suppose that the return on a risk-free loan is . Thus, we have the payout shown in Figure 16.5.

Figure 16.5 Single Period Payout Space

The call option will have the payout space given in Figure 16.6.

Figure 16.6 Call Payout Space

We want to use a combination of an investment in the stock and the risk-free asset to mimic the value of the call option. Letting Cu and Cd stand for the value of the call should the stock price rise or fall, respectively, then our aim is construct a riskless portfolio consisting of a long position of $x in the stock and $b in the risk-free asset plus a short position in one call option. If stock prices rise, we get the first of the following two equations; if they fall, we get the second equation. No arbitrage means that these will hold (otherwise, we can profit with no risk by selling ...