Chapter 4. IPv6 Subnetting
As I was going to St. Ives,
I met a man with seven wives,
Each wife had seven sacks,
Each sack had seven cats,
Each cat had seven kits:
Kits, cats, sacks, and wives,
How many were there going to St. Ives?
— Traditional Nursery Rhyme
Introduction
We’ve discussed how early efforts to successfully slow the depletion of IPv4 included techniques like VLSM, CIDR, and NAT. In particular, the granular subnetting provided by VLSM became a common (and engrained) practice in IPv4 network architecture and address planning. But the enormous scale of IPv6 and the resulting bounty of additional bits in a given address require new subnetting methods. These methods provide opportunities to improve both the ease and effectiveness of IPv6 address planning. In this chapter, we’ll cover these IPv6 subnetting techniques and the legacy IPv4 subnetting methods they differ from (and improve upon).
Subnetting IPv4: A Brief Review
Before we dig into IPv6 subnetting methods, let’s briefly review their counterparts in IPv4.
As we’ve already discussed, subnetting in IPv4 optimistically started out as class-based; i.e., using only two classes of subnets to facilitate aggregation and reduce the demand placed on router memory and CPU resources (as well as create some hierarchical consistency within the Internet).
The first two classes of subnets in IPv4 were as follows:
But as the Internet began to grow, most organizations discovered that they had an abundance of unused address space. In general, this situation was beneficial to them individually: they had plenty of addresses for current use and future growth, plus they could aggregate their networks efficiently and maintain improved router performance.
The situation was not so beneficial for the addressing needs of a rapidly expanding Internet. So class C networks were proposed as a way to allow for much more granular allocation to smaller organizations with more modest addressing requirements.
The 254 host addresses available in a class C network[68] made them ideal for assigning to organizations that had more modest host requirements, especially leaf or stub networks.
But many more organizations (especially small- and medium-sized ISPs) would need multiple class Cs for their host addressing, though perhaps not as much as an entire class B. Allocating more than 1 class C but fewer than 256 of them meant that there would potentially be many more routing table entries. In addition, for some network architectures and topologies, even a class C could end up being wasteful if assigned to one segment or interface.
Either way, even with class Cs, the classful addressing approach was simply not sophisticated enough to support sufficient host addressing and efficient routing. Some other mechanism would be needed to allow the aggregation of any number of smaller subnets into larger ones.
VLSM and CIDR provided this mechanism. It allowed for any number of the 32 bits of the IPv4 address to be used for the network ID while those bits that remained would define the host addressing. As an example, say we had a class C network that we wanted to use to number hosts on various segments:
192.0.2.0
Because it’s a class C, I know that I have 254 usable host addresses.
192.0.2.1 to 192.0.2.254
As with any IPv4 address, the subnet mask must accompany it so that it’s clear what bits are reserved for the network (with the remaining bits set aside for the hosts). The subnet mask for a class C looks like this:
255.255.255.0
The mask works by a bitwise logical AND operation:
192.0.2.55 = 11000000 00000000 00000010 00110111
255.255.255.0 = 11111111 11111111 11111111 00000000
———————————————————————————————————
Logical AND: 11000000 00000000 00000010 00000000You’ll notice that the host bits are “zeroed out” by the operation, while the network bits “pass through” the mask. Converting from binary back to decimal gives us:
192.0.2.0
In my hypothetical network, let’s stipulate that I have two segments that each have 50 servers and that I expect to grow by 25% a year for the next three years:[69]
50 + 3(50 x 0.25) = server count on segment after 3 years
After three years, neither segment will have more than 90 servers. I need enough bits to support a subnet with a host count of at least 90. According to binary math, the smallest subnet to support 90 servers is provided by 7 bits (though recall that I lose 2 addresses to the network and broadcast addresses):
![]()
90 servers using 126 available addresses equates to just a little above 70% utilization, so I’ve still got a little room for growth before I’ll potentially need to renumber.
Since we’ll need 7 bits for host addressing for each segment, that leaves 25 bits for the network, giving us the following subnet mask:
255.255.255.128
or
11111111 11111111 11111111 10000000
Recall that our original class C network had a mask of 255.255.255.0 and 24 bits.
The two possible values of the 25th bit give us two networks:
192.0.2.0 = 11000000 00000000 00000010 00000000
255.255.255.128 = 11111111 11111111 11111111 10000000
———————————————————————————————————
Logical AND: 11000000 00000000 00000010 00000000 = 192.0.2.0192.0.2.128 = 11000000 00000000 00000010 10000000
255.255.255.128 = 11111111 11111111 11111111 10000000
———————————————————————————————————
Logical AND: 11000000 00000000 00000010 10000000 = 192.0.2.128The 7 bits remaining provide 128 addresses, giving our two new networks 128 total addresses each:
192.0.2.0 to 192.0.2.127
and
192.0.2.128 to 192.0.2.255
Computers rely on binary operations that require the inclusion of a subnet mask whenever an IPv4 address is represented. It’s more convenient for humans to represent the subnet mask as either a dotted quad of octets (e.g., 255.255.255.0) or using CIDR notation; i.e., “/nn” notation where the network bits (represented by “nn”) of an address are appended to the end of the address after a “/” (e.g., 192.0.2.0/24). IPv6 uses CIDR notation exclusively.
The CIDR and VLSM methods led to a chain of significant design and operational consequences. Since it allowed for aggregation of networks beyond the 8-bit boundaries of the classful networks, the need for efficient aggregation and routing could be balanced against the need for sufficient host addressing.
This, in turn, led to the practice of defining and assigning to a link the smallest practical subnet to support immediate and anticipated host counts. Proper aggregation and efficient routing, while still possible, were more often a secondary concern (or a lucky accident). Thus, the definition of what makes a particular address plan efficient changed over time. It went from one that emphasized the importance of fewer routes in the routing table and consequent router resource conservation to one that emphasized the preservation of host addresses. As mentioned earlier, this is the essential element of IPv4 thinking.
A Note on Efficiency
The original challenge with IPv4 subnetting was defining and assigning subnets that provided sufficient host addresses per segment while at the same time not having too many unused addresses left over. We might have heard an address plan exclusively referred to as “efficient” merely because it provided sufficient IP addressing for the network.
But this form of efficiency is impossible to maintain and improve, given an ever-dwindling supply of addresses. Because it’s often not feasible to reliably predict how quickly any given network might grow, administrators could face either running out of available addresses on a segment and having to renumber in order to increase subnet size (or having underutilized subnet assignments tying up subnet bits that could be assigned elsewhere to support growth).[70]
In the first chapter, we reviewed the dilemma of scale and the difficulty of balancing the requirements of sufficient host addressing with efficient routing (e.g., conservation of router memory and CPU by aggregation of prefixes) in IPv4. IPv6 was designed in a way to eliminate the tension between these two requirements. It does this by first providing a standard interface subnet with 64 bits of host addressing. With 1.8x1019 addresses, overutilization of addresses on a single network interface simply isn’t possible. This, in turn, allows network engineers designing a site to aggregate interface subnets for, among other potential benefits, routing efficiency.
But what the heck do we need routing efficiency for anyway? To answer that is to get at why we need routing at all.
We often talk about networks being flat or hierarchical, where, in the simplest terms, the former suggests a switched network while the latter usually implies a routed one. Each type of network has pros and cons. Flat networks are simple. The flattest network is a collection of hosts sharing a transmission medium and communicating with each other directly. As long as I’ve got enough unique network addresses, switch ports, and bandwidth, I can keep adding hosts. That is, up to a point.
Eventually, however, the network becomes overloaded. The protocols allowing communication between the hosts have overhead that consumes bandwidth. The switch ports have to keep track of hardware addresses and have limited memory with which to do so. And we need some way of keeping those switches from forming loops and causing address table corruption and broadcast storms. The physical limitations of the transmission medium itself begin to interfere with reliable network state information once too great a distance separates hosts and latency increases.
It turns out that all networks require state information: Where are the hosts? What paths are available to connect them? Is a particular host still connected?
Network segmentation is a way of limiting the amount of state information that must be managed for a given collection of hosts. Routing was invented to help accomplish this by providing a way to aggregate host addresses and reduce the amount of state information any single router or switch had to manage and maintain. But beyond just overcoming the limitations of the networking equipment and physics, the hierarchy that results from segmentation and routing creates a logical framework that makes it much easier for humans to effectively manage and maintain networks.
Summarization creates logical boundaries that can be correlated to the administrative entities for which we created the networks in the first place. These boundaries are essential for making distinctions about what constitutes the inside and outside of the network (and which side a given host or set of networks should be on). From these distinctions, administrative responsibilities and lines of demarcation are established. Security policies are designed and instantiated. And so it goes.
These logical boundaries facilitated by summarization are much easier to establish in IPv6. And because renumbering and resubnetting to support changes in interface host counts are no longer necessary, such logical boundaries are also much easier to maintain over time.
With IPv6, host address conservation (and whatever limited form of efficiency it provided) is effectively obsolete. We can now optimize our design choices for the superior efficiencies of network scale and operational ease.
Nibble Boundaries
A nibble is 4 bits. Since IPv6 addresses are expressed using hexadecimal characters, subnetting exclusively in multiples of four bits has several important benefits for address planning (and operations).
The first and most obvious of these is that our CIDR notation for any prefix will always be a multiple of four. For example, starting from a /64 (as that’s the smallest typical subnet size):
/64, /60, /56, /52, /48, /44, etc.
From an operational standpoint, this makes any subnetting transcription errors in configuration or documentation immediately apparent. For example:
/53, /47, /39, etc.
The next benefit is that we have a smaller possible set of subnet groups to account for, as shown in Table 4-1:.
As we get into our address plan design based on our network topology, it’s uncommon that we’ll have any network entities (VLANs, buildings, business units, etc.) in groups larger than 65536.
Also, much of our address planning will be focused on either the 16 bits of the individual site subnet ID (from /48 to /64) or the 16 bits of the overall organizational assignment (typically from /32 to /48, though possibly larger for the largest enterprises). As a result, the first four values (i.e., 16, 256, 4096, and 65536) are the most often used and thus most usefully remembered.
The final benefit takes a bit more explaining.
Prefix Legibility
The final benefit of adhering to the nibble boundary when subnetting in IPv6 is improved prefix legibility (or, to put it another way, human-readability).
What do we mean by legibility? Let’s demonstrate with an example. Say we’ve been assigned a /48 for the headquarters site of a large enterprise. (We’ll explain in detail why we might get such an assignment in Chapter 5.)
The site has 20 buildings, and we’ve designed our plan to allocate one subnet per building. (We’ve been told to anticipate very little growth as the company is planning on moving the HQ sometime in the next two to five years.) We’ll set aside an additional subnet for infrastructure between buildings for a total of 21 subnets.
The minimum number of bits we’d need to use to support 21 subnets would be 5, which gives us a total of 32 subnets. We’ve got 11 subnets to spare in case any need arises to assign additional ones. The Ns represent these 5 bits below, while the Xs are unspecified:
2001:db8:abcd:[NNNNNXXXXXXXXXXX]::/53
Note that while this provides sufficient subnets, the resulting prefixes aren’t as immediately legible because the bit boundary doesn’t align with the 4 bits used to define the hexadecimal character in the address:
2001:db8:abcd:0000::/53 2001:db8:abcd:0800::/53 2001:db8:abcd:1000::/53 2001:db8:abcd:1800::/53 ...
Continuing with our example, the abundance of addresses available in IPv6 allows us to use 8 bits (instead of only 5), which makes the hexadecimal representation of the resulting subnets much tidier:
2001:db8:abcd:000::/56 2001:db8:abcd:100::/56 2001:db8:abcd:200::/56 2001:db8:abcd:300::/56 ...
For each subnet group, only one value is possible for the hexadecimal character that corresponds to the 4-bit boundary in the IPv6 prefix (in this case, a /56). This makes the resulting prefix more immediately readable.
Obviously, the use of more bits gives us more subnets: 256 in this case, 21 of which we’ll use immediately along with 235 for future use. But fewer host ID bits also reduces the number of available /64 subnets in each parent subnet. In our above example, we went from 2048 /64s available per /53 to 256 /64s available with a /56.
Visualizing Hierarchy
As mentioned in the last section, much of our address planning will be focused on either the 16 bits of the individual site subnet ID (from /48 to /64) or the 16 bits of the overall organizational assignment (typically from /32 to /48).
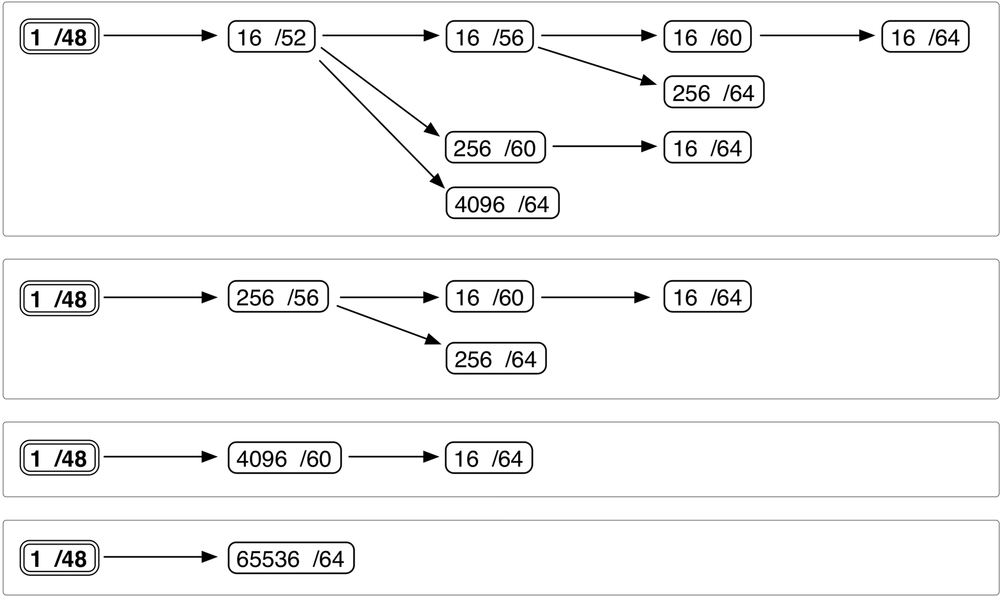
As it turns out, dividing either of these 16-bit groups along their nibble boundaries gives us a very simple way of visualizing the hierarchy available to us when defining our addressing plan. We’ll pick the typical subnet ID range to demonstrate, i.e., /48 to /64 (Figure 4-1).
To create an IPv6 subnetting hierarchy from a /48 using the above diagram, simply choose one of the four boxes and then a single path in that box from left to right.
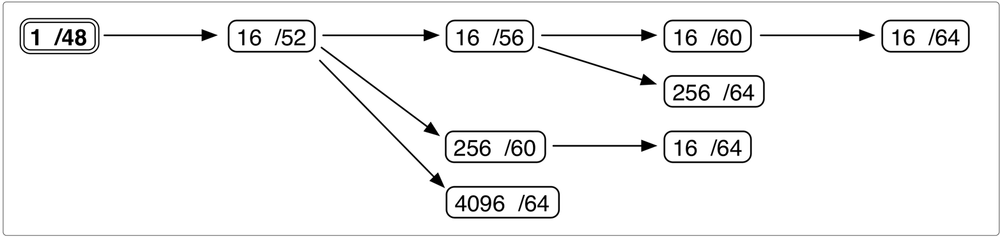
The first box gives us four unique possibilities, as shown in Figure 4-2:
Box two provides two possible paths (Figure 4-3):
One path each is provided by the third and fourth boxes (Figure 4-4):
Adding the possibilities up, we end up with only eight paths to choose from.
As it happens, this simple expression of subnetting hierarchy will often prove more than adequate to guide a basic topology for many organizations. It strikes a good balance between the minimum amount of complexity required to instantiate operational efficiency and the simplicity to make and keep the plan extensible and flexible.
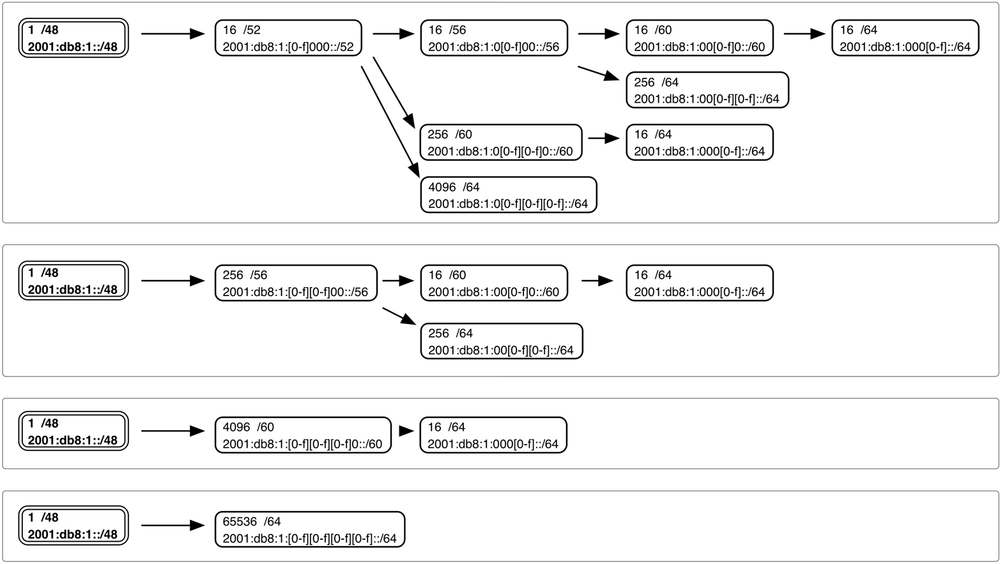
Let’s take a look at the same figure with actual subnets added for clarity (Figure 4-5):
In this figure, the range of possible values to enumerate the subnets available at that level of hierarchy is bracketed. For example, starting in the upper left-hand corner and moving to the right, we observe that the 16 /52s at that level will be enumerated by modifying the first character of the fourth hextet:
2001:db8:1::/52 (or, expanded for clarity, 2001:db8:1:0000::/52) 2001:db8:1:1000::/52 2001:db8:1:2000::/52 ... 2001:db8:1:F000::/52
From there, each of our /52s could be further subnetted along one of three different paths.
The first path gives us 16 /56s enumerated by the second character (and next 4 bits) of the fourth hextet. Choosing the first /52 from the step above, we get the first group of 16 /56 subnets:
2001:db8:1::/56 2001:db8:1:0100::/56 2001:db8:1:0200::/56 ... 2001:db8:1:0F00::/56
The second group of 16 /56 subnets would be:
2001:db8:1:1000::/56 2001:db8:1:1100::/56 2001:db8:1:1200::/56 ... 2001:db8:1:1F00::/56
The second path gives us 256 /60s enumerated by the second and third character (and 8 middle bits) of the fourth hextet. Again choosing the first /52 subnet from our first example, we get the first group of 256 /60 subnets:
2001:db8:1::/60 2001:db8:1:0100::/60 2001:db8:1:0200::/60 ... 2001:db8:1:0FF0::/60
The second group of 256 /60 subnets would be:
2001:db8:1:1000::/60 2001:db8:1:1100::/60 2001:db8:1:1200::/60 ... 2001:db8:1:1FF0::/60
The final path gives us 4096 /64s enumerated by the second, third, and fourth characters (and right-most 12 bits) of the fourth hextet. Once more, starting with the first /52 subnet, we get the first group of 4096 /64 subnets:
2001:db8:1::/64 2001:db8:1:0100::/64 2001:db8:1:0200::/64 ... 2001:db8:1:0FFF::/64
The second group of 4096 /64 subnets would be:
2001:db8:1:1000::/64 2001:db8:1:1100::/64 2001:db8:1:1200::/64 ... 2001:db8:1:1FFF::/64
Hopefully, these images (and the method associated with them) give you a better sense of how to visualize and enumerate the subnets and hierarchy options available to you for a site. With a few uses, you’ll quickly be able to mentally map out your options.[72]
Non-Nibble Subnetting
As we discussed, we’ll want to use nibble boundary subnetting whenever possible. Recall that if we stick to the nibble boundary when subnetting a site prefix with 16 bits, we always get 16, 256, 4096, or 65536 prefixes. Also, enumeration is simple, as each hexadecimal character represents a nibble and prefixes will never “divide” a hex character.
However, there may be instances that arise where we’ll need to use the non-nibble “in-between” bits to provide sufficient subnets for our site address plan.
Here’s a method for IPv6 subnetting using any number of bits in the subnet ID. This will allow you to calculate and enumerate groups of prefixes other than the ones adhering to nibble boundaries, i.e., 16, 256, 4096, 65536, etc.[73]
Let’s walk through this method with an example allocation. Say we’ve received 2001:db8:abba::/48 to number a campus LAN.
With a little planning, we’ve determined that we’re going to need at least 16 subnets for each building. So this first group of prefixes will not require our method because we simply adhere to the 4 bits of the first nibble boundary.
This gives us 16 prefixes enumerated by the first character of our fourth hextet:
2001:db8:abba::/52 2001:db8:abba:1000::/52 2001:db8:abba:2000::/52 ... 2001:db8:abba:f000::/52
Now, let’s say for the sake of illustration that our typical campus building uses 20 VLANs. Since allocating 4 more bits to take us to the next nibble boundary only yields 16 additional prefixes, we’ll need more than 4 bits. By standard IPv6 address planning principles, we should be entirely comfortable simply allocating an additional 4 bits for a total of 8 bits. This would give us 256 additional prefixes (with 4 bits remaining for 16 /64s per prefix). But to demonstrate our method, let’s get more granular and only use as many bits as gives us sufficient prefixes for the number of elements in this level of our design (i.e., 20 VLANs). Since the least number of bits that produces an integer value greater than 20 is 5 (25 = 32), we’ll use 5 bits to subnet our /52 prefix.
First, where p = prefix length of the parent subnet and a = number of fixed bits in the subnet ID:
a = p - 48
From our example:
a = 52 - 48 = 4
a = 4
So we have 4 bits that are fixed (which we already knew, but the value is used in later formulae).
Next, where s = subnets created and b = bits used to subnet
s = 2b
s = 25 = 32
s = 32
As we outlined above, we’ll create 32 subnets using 5 bits.
Next, where i = the (decimal) increment value between the created subnets (which we must convert back to hexadecimal):
i = 216-(a+b)
i = 216-(4+5) = 216-9 = 27 = 128
i = 128
Converted to hexadecimal:
i = 0x80
Next, where p1 = the prefix length of the created subnets:
p1 = 48 + a + b
p1 = 48 + 4 + 5 = 57
So now that we know the increment and prefix length value, we can enumerate the new subnets:
2001:db8:abba::/57 2001:db8:abba:80::/57 2001:db8:abba:100::/57 2001:db8:abba:180::/57 ... 2001:db8:abba:f80::/57
Et voilà: Our 32 new subnets.
We could, of course, subnet each of these /57s further in order to provide additional hierarchy for other organizational or operational requirements.
But assuming we don’t, how many /64 interface subnets would each of these /57s provide?
Finally, where n = number of /64 subnets provided by each new subnet:
n = 2(64-p1)
n = 2(64-57) = 27 = 128
So each /57 will provide us with 128 /64 interface subnets.
With a little practice, you’ll be able to dispense with the formulae and do this in your head.
A Bit to the Left, a Bit to the Right
There are many bit-allocation methods to help take advantage of the tremendous subnetting flexibility in IPv6. It’s a Good Thing™, too, because there are many sizes of networks with many different business requirements. And, of course, networks are constantly growing, shrinking, adding new applications and services, etc. As a result, it’s sometimes difficult to know in advance what size allocations will be ideal for an existing or planned set of networks. (We’ll review IPv6 address allocation methods in the next chapter.)
Let’s look at three ways we could assign bits in an allocation to create subnets. We’ll start with a sample allocation:
2001:db8:aa00::/40
The same allocation expressed in binary:
00100000 00000001 00001101 10111000 10101010 00000000
For illustration purposes, we’ll focus on the next 8 bits available to us (from /41 to /48). Keep in mind that the maximum number of subnets with 8 bits is 256.
Subnets from the Right-Most Bits
The first method would be to begin with and increment the right-most available bits (Table 4-2):
Name | Binary | Hex |
Subnet1 | 00000000 | 2001:db8:aa00::/48 |
Subnet2 | 00000001 | 2001:db8:aa01::/48 |
Subnet3 | 00000010 | 2001:db8:aa02::/48 |
Subnet4 | 00000011 | 2001:db8:aa03::/48 |
… | … | … |
Subnet256 | 11111111 | 2001:db8:aaff::/48 |
This method has some advantages. It’s certainly the simplest of the allocation methods. A major disadvantage, however, is that if an allocation turns out to be too small to accommodate growth, there is no easy way to increase its size contiguously.[74]
Subnets from the Left-Most Bits
The second method starts from the left-most available bits and assigns them from left to right (Table 4-3).
Name | Binary | Hex |
Subnet1 | 00000000 | 2001:0db8:aa00::/48 |
Subnet2 | 10000000 | 2001:0db8:aa80::/48 |
Subnet3 | 01000000 | 2001:0db8:aa40::/48 |
Subnet4 | 11000000 | 2001:0db8:aac0::/48 |
Subnet5 | 00100000 | 2001:0db8:aa20::/48 |
… | … | … |
Subnet256 | 11111111 | 2001:0db8:aaff::/48 |
It’s hard to perfectly visualize, but it’s pretty obvious that early in our list there is plenty of space between subnets. (Although as we assign bits from left to right, we would eventually account for every possible subnet and fill in the space between the prefixes at the start of our list.)
The disadvantage here is that since we’ve started with the left-most bits, we’re right at the edge of our allocation. We can always create smaller subnets, but there’s no way to create any larger subnets, contiguous or otherwise.
Can you guess where the third method begins? That’s right! With the middle bits!
Subnets from the Middle Bits
The algorithm for assigning bits for this method is a little more complex.[75]
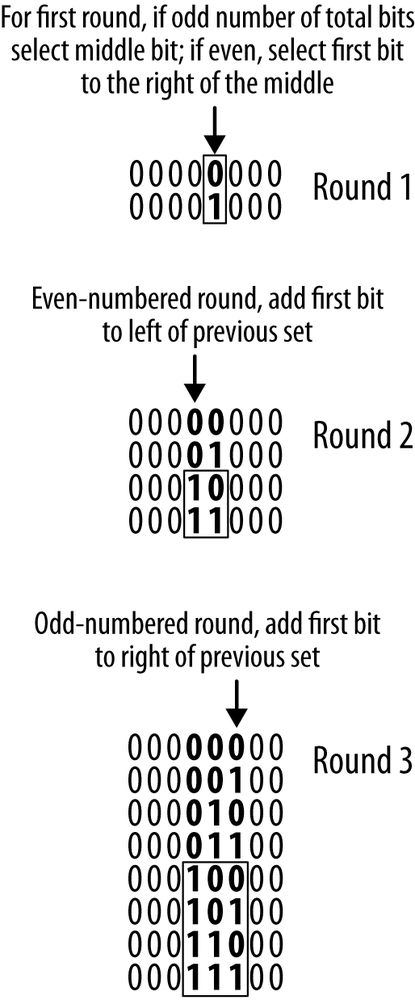
If we have an odd number of bits, we start with the middle one:
000000000
If we have an even number of bits (as we do in our example), we divide them in half and choose the left-most bit of the second half:
00000000
Next, we count up through the available bits in our set. Since we’ve only selected one bit so far, there are only two possibilities:
00000000 00001000
In our example, these would correspond to the following subnets:
2001:db8:aa00::/48 2001:db8:aa08::/48
We now say that we’ve completed the first round of bit selection and subnetting.
Each subsequent round will add an additional bit to the previous round’s set of bits. If we’re in an even-numbered round, we add the first available bit to the left of our previous set. If we’re in an odd-numbered round, we add the first available bit to the right of the previous round’s bit set. Then we count up through all the available bits in that set. Rinse. Repeat. (See Figure 4-6.)
The power of this method is two-fold.
By leaving unused bits to the left, we’re effectively leaving space between subnets. By numbering into these bits, we can arbitrarily increase the size of a previous allocation.
By leaving unused bits to the right, we can create smaller subnets as needed.
Perhaps we could refer to this as tentative allocation. If all or part of our network is very dynamic, we might reasonably infer that we’ll have to modify our allocation scheme to accommodate any change and growth. This method gives us a way to do it more easily.
Since this method is a bit more involved, there are multiple tools available to help manage it (including ipv6gen, detailed below).
Using Only Numeric Subnets
We’ve seen how subnetting from the left-most or middle bits can leave ample space between subnets for future use. Another way to preserve space in a group is to select those subnets containing only numbers (and no hexadecimal characters).
For example:
2001:db8:abba:0[0-9][0-9]0::/56
Enumerating the numbers-only subnets would give us blocks of /60s, according to the following pattern:
2001:db8:abba::/60 2001:db8:abba:0010:/60 2001:db8:abba:0020:/60 ... 2001:db8:abba:0090:/60
Here are the subnets containing hexadecimal characters from the same range:
2001:db8:abba:00a0:/60 2001:db8:abba:00b0:/60 2001:db8:abba:00c0:/60 ... 2001:db8:abba:00f0:/60
Out of the 256 total subnets available, 100 numeral-only subnets would be used. This method leaves 61% of any group of subnets in reserve for future use. (It’s also helpful operationally because production subnets are immediately identifiable by the absence of hexadecimal characters in a given group.)
ipv6gen
ipv6gen is a very handy open-source, Perl-based tool for generating and enumerating subnets from a larger prefix.
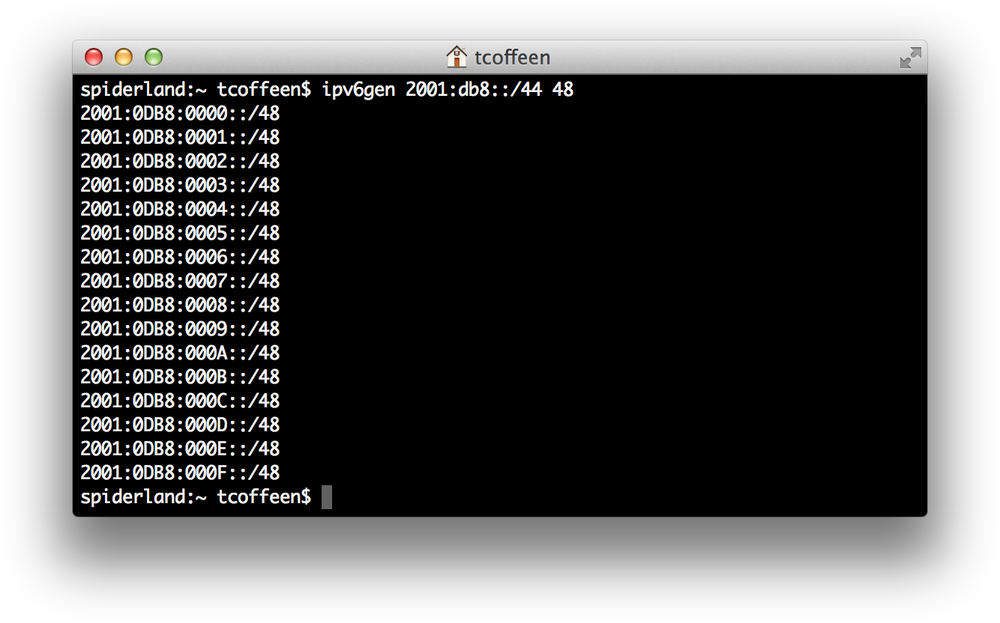
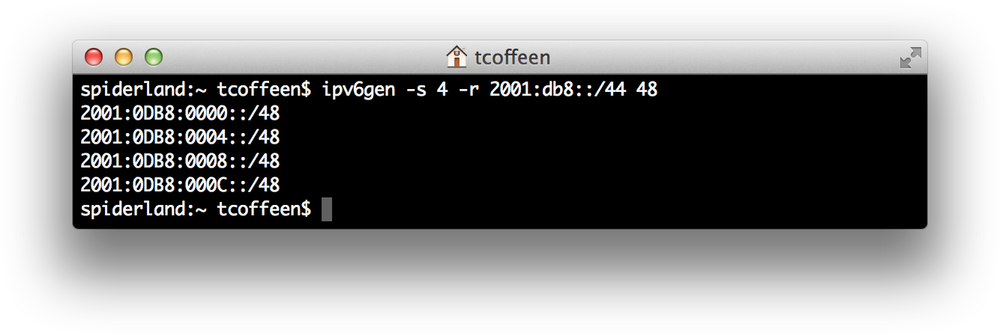
You enter the prefix you want to subnet, as well as the size of the prefixes you want to generate (Figure 4-7).
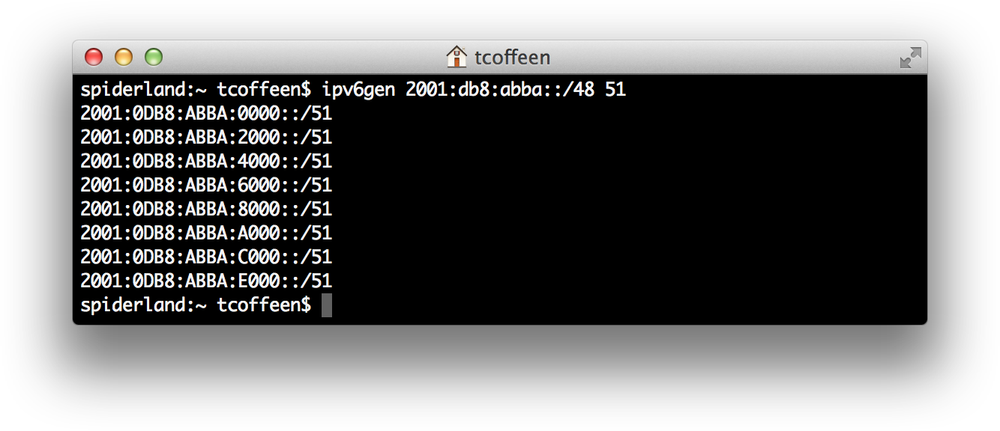
It’s especially useful for accurately enumerating prefixes when subnetting away from the nibble boundary (Figure 4-8).
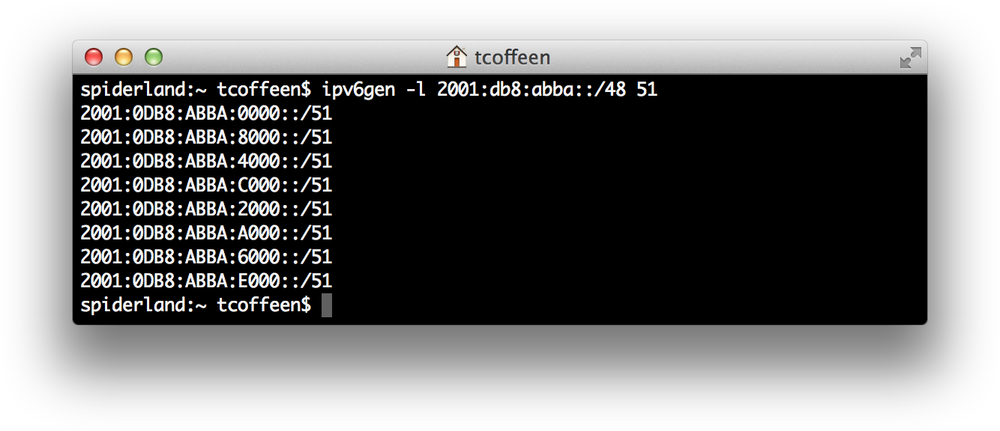
With no argument, ipv6gen allocates from the right-most bits of the entered prefix. But the tool also lets you allocate from the left-most bits, which is a useful approach if you think you might need to create additional contiguous subnets in the future (Figure 4-9).
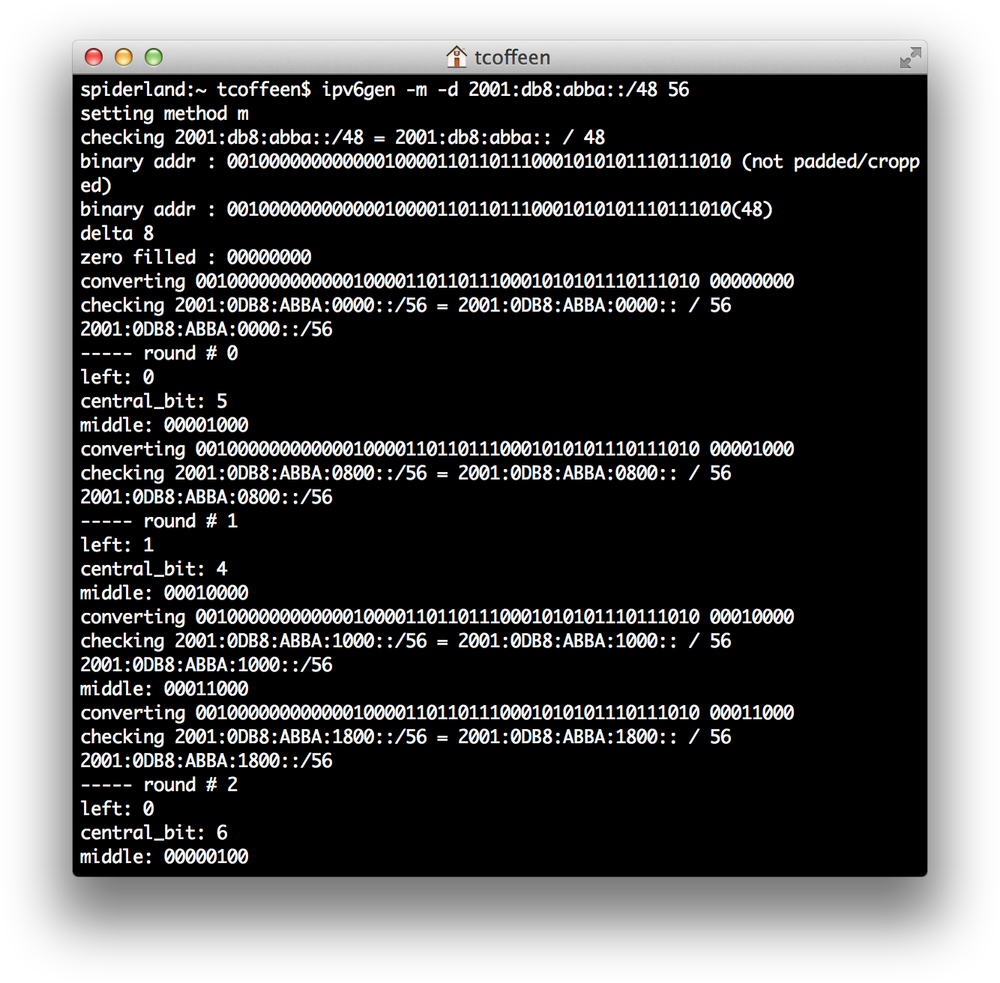
Finally, you can allocate from the middle bits, allowing contiguous subnetting for both larger and smaller prefixes (shown here with the debug flag set in Figure 4-10).
ipv6gen also has a sparse allocation function that skips the enumeration of intervening prefixes. Here’s the example from Figure 4-7 using the “step between prefixes” argument set to 4 (Figure 4-11).
For each prefix, the three prefixes that would have followed are dropped. These prefixes could be held in reserve and allowed for future assignment and aggregation (in this example, to a /46).
[68] Recall that the first and last addresses of any subnet (in this case .0 and .255) are reserved for the network and broadcast addresses respectively.
[69] Sorry, no compound interest.
[70] Notice that this approach leaves aggregation to facilitate routing and security policy as an afterthought.
[71] Recall that data plane performance is enhanced by pushing routing information down to an individual port’s FIB (forwarding information base). Each port has a limited amount of ternary content addressable memory (TCAM) to store its FIB. As a result, per-port costs are dependent on the amount of TCAM needed, which proper prefix aggregation can help reduce.
[72] As mentioned, this approach will work just as well for the 16 bits between a /32 and a /48 (thus, for any address planning necessary between sites).
[73] This method is derived in part from the one presented in Joseph Davies’ excellent book Understanding IPv6: Your Essential Guide to IPv6 on Windows.
[74] You may notice, however, that when using this method, by simply skipping some fixed number of subnets in between allocations, you’ll automatically leave subnets in reserve for future contiguous assignments. For example, start at 2001:db8:aa01::/48 and allocate every other prefix: 2001:db8:aa03::/48, 2001:db8:aa05::/48, etc. That would leave in reserve 2001:db8:aa00::/48, 2001:db8:aa02::/48, 2001:db8:aa04::/48, etc. The CLI tool ipv6gen, which is used for automatically generating IPv6 subnets, offers this capability. We’ll examine this, as well as other features of ipv6gen, in more detail at the end of this chapter.
Get IPv6 Address Planning now with the O’Reilly learning platform.
O’Reilly members experience books, live events, courses curated by job role, and more from O’Reilly and nearly 200 top publishers.