Jakarta Commons Cookbook

4.9. Creating Composite Predicates

Problem

You need to perform complex conditional logic using multiple Predicate objects, and you need to combine and expose multiple criteria as one Predicate.

Solution

To combine several Predicate instances, create a Predicate to capture each portion of a compound condition, and combine each condition with AndPredicate, OrPredicate, AllPredicate, OnePredicate, AnyPredicate, or NonePredicate. All of these predicate implementations are used to combine the results of multiple predicates—creating a compound predicate. The following code demonstrates the use of the AndPredicate, OrPredicate, AllPredicate, and OnePredicate:

import org.apache.commons.collections.Predicate;
import org.apache.commons.collections.functors.*;

// Create Base Predicates
Predicate isTim = new EqualsPredicate("Tim");
Predicate isDouble = new InstanceOfPredicate( Double.class );
Predicate isNotNull = NotNullPredicate.INSTANCE;

Predicate[] predicates = new Predicate[] { isTim, isDouble, isNotNull };

// Create 2 argument logical predicate composites
               Predicate andPredicate = new AndPredicate( isTim, isNotNull );
               Predicate orPredicate = new OrPredicate( isTim, isNotNull );

               // Create n-argument logical predicate composites
               Predicate allPredicate = new AllPredicate( predicates );
               Predicate onePredicate = new OnePredicate( predicates );

System.out.println( "'Tim' and not null?: " + andPredicate.
evalute( "Tim" ) );
System.out.println( "'Tim' or not null?: " + andPredicate.
evalute(new Long(3))); 

System.out.println( "'Tim', not null, and Double?: " 
                        + allPredicate.evaluate( "Impossible" ) );
System.out.println( "XOR ('Tim', not null, or Double?): " 
                        + allPredicate.evaluate( "Impossible" ) );

This example creates the following output:

'Tim' and not null?: true
'Tim' or not null?: true

'Tim', not null, and Double?: false
XOR('Tim', not null, or Double?): true

Discussion

An AndPredicate returns true if both predicates supplied to its constructor return true, and an OrPredicate returns true if at least one of the two predicates passed to its constructor returns true. An AllPredicate takes an array of predicates, only returning true if every predicate evaluates to true. The OnePredicate also takes an array of predicates, only returning true if exactly one predicate evaluates to true.

In the code sample, the use of the second to last predicate, AllPredicate, is impossible to satisfy; an object can never be a String and a Double at the same time. This example fails to demonstrate AnyPredicate and NonePredicate—both take an array of predicates. AnyPredicate returns true if any of the predicates evaluate to true, and NonePredicate returns true only if none of the predicates evaluate to true. The behavior of these objects is easily inferred from the names: And, Or, All, One, Any, or None.

Any logical expression can be modeled by connecting Predicate objects together— similar to the way that simple logic gates are connected to create complex digital logic. Logical inputs (1 and 0) are routed to logic gates (AND, OR, NOR, NAND, XOR, etc.), and the outputs of a logic circuit are a result of stages that perform the same function as the Predicate objects introduced in this recipe. In the next example, a logic circuit will be used to demonstrate a complex hierarchy of Predicate objects; a circuit diagram is drawn, and a series of predicates are developed to model this circuit. Figure 4-1 contains a logical expression that is implemented with digital logic and Predicate objects.

Figure 4-1. Logical expression to be modeled with Predicate

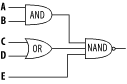
Assuming that every letter corresponds to a boolean variable, this expression corresponds to the circuit diagram in Figure 4-2. Each gate can be modeled as a composite Predicate, and from Figure 4-2 it is clear that this example will include two AndPredicates, an OrPredicate, and a NotPredicate. The “AND” gate is modeled with an AndPredicate, and an “OR” gate with an OrPredicate. The “NAND” gate is transformed into a three-input “AND” gate followed by an inverter that is modeled with an AllPredicate wrapped in a NotPredicate.

Figure 4-2. Circuit representing logical expression

The system has five inputs, which will be stored in a Map with five keys: A, B, C, D, and E. A simple InputPredicate is developed to handle the inputs to the system—a map of Boolean input objects is passed to the top-level Predicate. An InputPredicate is configured to evaluate the input Map and return the boolean value of one of the inputs; in other words, an InputPredicate selects a boolean value from a Map, always returning the value of that input from the Map it evaluates. (See Example 4-7.)

Example 4-7. InputPredicate: a predicate that selects an input from a Map

package com.discursive.jccook.collections.predicate;

import org.apache.commons.collections.Predicate;

public class InputPredicate implements Predicate {

    private String inputKey;

    public BooleanPredicate(String inputKey) {
        this.inputKey = inputKey;
    }

    public boolean evaluate(Object object) {
        boolean satisfies = false;

            Map inputMap = (Map) object;
        Boolean input = (Boolean) inputMap.get( inputKey );
        if( input != null ) {
            satisfies = input.booleanValue( );
        }

        return satisfies;
    }
}

The entire circuit is modeled by one top-level Predicate and a Map of Boolean input signals is passed down a hierarchy of predicates as needed. Unlike a real circuit, where inputs would cause gates to fire sequentially, the predicate hierarchy is evaluated from the final stage backward—the example evaluates the Predicate variable circuit. The input map is passed to the top-most Predicate, which, in turn, passes this same map to the Predicate that precedes it in the circuit. Example 4-8 ties everything together, and the logic to create our circuit-modeling predicate has been confined to the createPredicate() method.

Example 4-8. Implementing a multilevel composite Predicate

package com.discursive.jccook.collections.predicate;

import org.apache.commons.collections.Predicate;
import org.apache.commons.collections.functors.*;

public class CompoundPredicateExample {

    public static void main(String[] args) {
        CompoundPredicateExample example = new CompoundPredicateExample( );
        example.start( );
    }

    public void start( ) {

        Predicate circuit = createPredicate( );
                         Object[] inputsArray = 
                             new Object[][] { {"A", Boolean.TRUE},
                                              {"B", Boolean.FALSE},
                                              {"C", Boolean.TRUE},
                                              {"D", Boolean.FALSE},
                                              {"E", Boolean.FALSE} };
                          Map inputs = ArrayUtils.toMap( inputsArray );
                          boolean result = circuit.evaluate( inputs ); 

                           System.out.println( "The circuit fired?: " + result );
                      }

    public Predicate createPredicate( ) {
        Predicate aPredicate = new InputPredicate("A");
        Predicate bPredicate = new InputPredicate("B");
        Predicate cPredicate = new InputPredicate("C");
        Predicate dPredicate = new InputPredicate("D");
        Predicate ePredicate = new InputPredicate("E");

        Predicate expression1 = new AndPredicate( aPredicate, bPredicate );
        Predicate expression2 = new OrPredicate( cPredicate, dPredicate );

       Predicate[] secondLevel = 
           new Predicate( ) { expression1, expression2, ePredicate };

       Predicate topLevel = new NotPredicate( secondLevel );
       return topLevel;
    }
}

This code prints The circuit fired?: true. This complex example has demonstrated the process of modeling composite, multistage logic with a hierarchy of predicates. A Predicate is the most basic functor and when combined with other Predicate instances, there is no limit to the level of complexity that can be achieved. Logic circuits were used in this example because a logic gate is a great analogy for a Predicate. Think of a Predicate as a component—a gate in a logic circuit.