Learning OpenCV

LogPolar

For two-dimensional images, the log-polar transform [Schwartz80] is a change from Cartesian to polar coordinates:

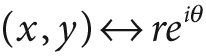
, where

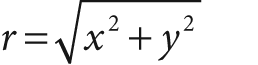
and

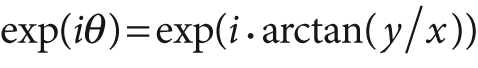
. Next, to separate out the polar coordinates into a (ρ, θ) space that is relative to some center point (x_c, y_c), we take the log so that

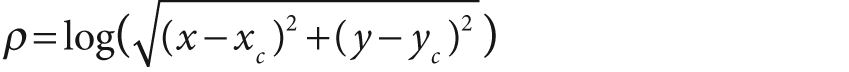
and

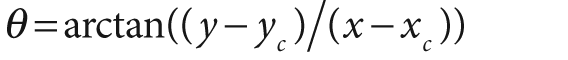
. For image purposes—when we need to "fit" the interesting stuff into the available image memory—we typically apply a scaling factor m to ρ. Figure 6-15 shows a square object on the left and its encoding in log-polar space.

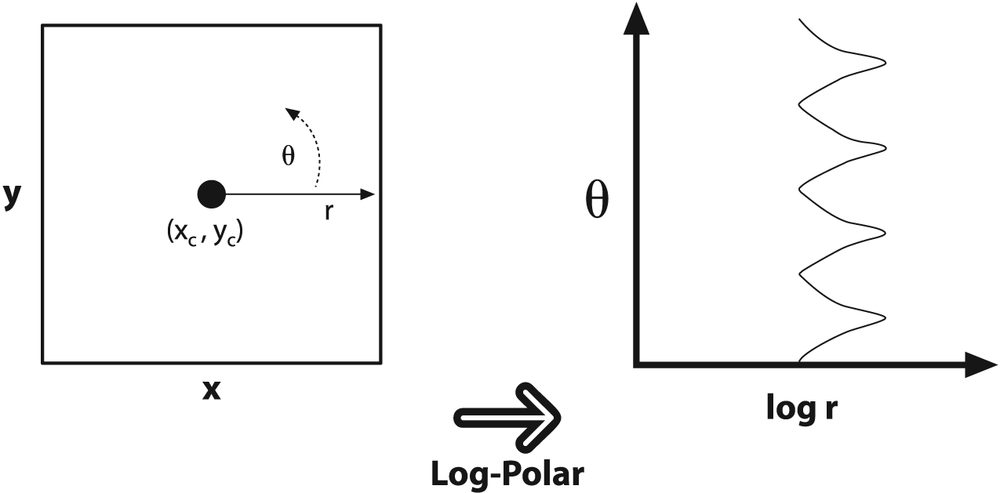
Figure 6-15. The log-polar transform maps (x, y) into (log(r),θ); here, a square is displayed in the log-polar coordinate system

The next question is, of course, "Why bother?" The log-polar transform takes its inspiration from the human visual system. Your eye has a small but dense center of photoreceptors in its center (the fovea), and the density of receptors fall off rapidly (exponentially) from ...