Learning OpenCV

Delaunay Triangulation, Voronoi Tesselation

Delaunay triangulation is a technique invented in 1934 [Delaunay34] for connecting points in a space into triangular groups such that the minimum angle of all the angles in the triangulation is a maximum. This means that Delaunay triangulation tries to avoid long skinny triangles when triangulating points. See Figure 9-12 to get the gist of triangulation, which is done in such a way that any circle that is fit to the points at the vertices of any given triangle contains no other vertices. This is called the circum-circle property (panel c in the figure).

For computational efficiency, the Delaunay algorithm invents a far-away outer bounding triangle from which the algorithm starts. Figure 9-12(b) represents the fictitious outer triangle by dotted lines going out to its vertex. Figure 9-12(c) shows some examples of the circum-circle property, including one of the circles linking two outer points of the real data to one of the vertices of the fictitious external triangle.

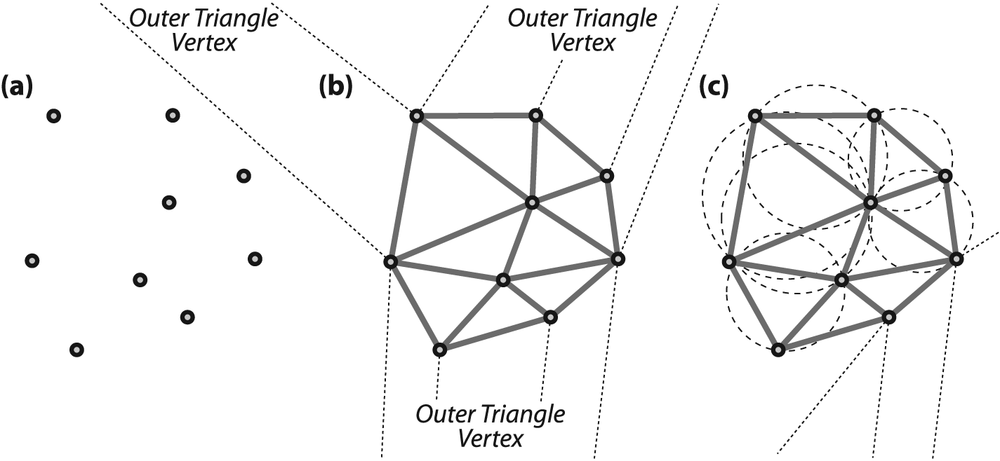
Figure 9-12. Delaunay triangulation: (a) set of points; (b) Delaunay triangulation of the point set with trailers to the outer bounding triangle; (c) example circles showing the circum-circle property

There are now many algorithms to compute Delaunay triangulation; some are very efficient but with difficult internal details. The gist of one of the more simple algorithms is as ...