Learning Python, 2nd Edition

Chapter 4. Numbers

This chapter begins our tour of the Python language. In Python, data takes the form of objects—either built-in objects that Python provides, or objects we create using Python and C tools. Since objects are the most fundamental notion in Python programming, we’ll start this chapter with a survey of Python’s built-in object types before concentrating on numbers.

Python Program Structure

By way of introduction, let’s first get a clear picture of how this chapter fits into the overall Python picture. From a more concrete perspective, Python programs can be decomposed into modules, statements, expressions, and objects, as follows:

1. Programs are composed of modules.

2. Modules contain statements.

3. Statements contain expressions.

4. Expressions create and process objects.

We introduced the highest level of this hierarchy when we learned about modules in Chapter 3. This part’s chapters begin at the bottom, exploring both built-in objects, and the expressions you can code to use them.

Why Use Built-in Types?

If you’ve used lower-level languages such as C or C++, you know that much of your work centers on implementing objects—also known as data structures—to represent the components in your application’s domain. You need to lay out memory structures, manage memory allocation, implement search and access routines, and so on. These chores are about as tedious (and error prone) as they sound, and usually distract from your programs’ real goals.

In typical Python programs, most of this grunt work goes away. Because Python provides powerful object types as an intrinsic part of the language, there’s no need to code object implementations before you start solving problems. In fact, unless you have a need for special processing that built-in types don’t provide, you’re almost always better off using a built-in object instead of implementing your own. Here are some reasons why:

• Built-in objects make simple programs easy to write. For simple tasks, built-in types are often all you need to represent the structure of problem domains. Because you get things such as collections (lists) and search tables (dictionaries) for free, you can use them immediately. You can get a lot of work done with Python’s built-in object types alone.

• Python provides objects and supports extensions. In some ways, Python borrows both from languages that rely on built-in tools (e.g., LISP), and languages that rely on the programmer to provide tool implementations or frameworks of their own (e.g., C++). Although you can implement unique object types in Python, you don’t need to do so just to get started. Moreover, because Python’s built-ins are standard, they’re always the same; frameworks tend to differ from site to site.

• Built-in objects are components of extensions. For more complex tasks you still may need to provide your own objects, using Python statements or C language interfaces. But as we’ll see in later parts, objects implemented manually are often built on top of built-in types such as lists and dictionaries. For instance, a stack data structure may be implemented as a class that manages a built-in list.

• Built-in objects are often more efficient than custom data structures. Python’s built-in types employ already optimized data structure algorithms that are implemented in C for speed. Although you can write similar object types on your own, you’ll usually be hard-pressed to get the level of performance built-in object types provide.

In other words, not only do built-in object types make programming easier, they’re also more powerful and efficient than most of what can be created from scratch. Regardless of whether you implement new object types or not, built-in objects form the core of every Python program.

Table 4-1 previews the built-in object types and some of the syntax used to code their literals— expressions that generate objects.^[1] Some of these types will probably seem familiar if you’ve used other languages. For instance, numbers and strings represent numeric and textual values, respectively, and files provide an interface for processing files stored on your computer.

Table 4-1. Built-in objects preview

Object type	Example literals/creation
Numbers	3.1415, 1234, 999L, 3+4j
Strings	'spam', "guido's"
Lists	[1, [2, 'three'], 4]
Dictionaries	{'food': 'spam', 'taste': 'yum'}
Tuples	(1,'spam', 4, 'U')
Files	text = open('eggs', 'r').read( )

The object types in Table 4-1 are more general and powerful than what you may be accustomed to. For instance, you’ll find that lists and dictionaries obviate most of the work you do to support collections and searching in lower-level languages. Lists are ordered collections of other objects, and indexed by positions that start at 0. Dictionaries are collections of other objects that are indexed by key instead of position. Both dictionaries and lists may be nested, can grow and shrink on demand, and may contain objects of any type. For the full story, though, you’ll have to read on.

Numbers

The first object type on the tour is Python numbers. In general, Python’s number types are fairly typical and will seem familiar if you’ve used almost any other programming language in the past. They can be used to keep track of your bank balance, the distance to Mars, the number of visitors to your web site, and just about any other numeric quantity.

Python supports the usual numeric types (known as integer and floating point), as well as literals for creating numbers, and expressions for processing them. In addition, Python provides more advanced numeric programming support, including a complex number type, an unlimited precision integer, and a variety of numeric tool libraries. The next few sections give an overview of the numeric support in Python.

Number Literals

Among its basic types, Python supports the usual numeric types: both integer and floating-point numbers, and all their associated syntax and operations. Like the C language, Python also allows you to write integers using hexadecimal and octal literals. Unlike C, Python also has a complex number type, as well as a long integer type with unlimited precision (it can grow to have as many digits as your memory space allows). Table 4-2 shows what Python’s numeric types look like when written out in a program (that is, as literals).

Table 4-2. Numeric literals

Literal	Interpretation
1234, -24, 0	Normal integers (C longs)
9999999999999999999L	Long integers (unlimited size)
1.23, 3.14e-10, 4E210, 4.0e+210	Floating-point (C doubles)
0177, 0x9ff, 0XFF	Octal and hex literals
3+4j, 3.0+4.0j, 3J	Complex number literals

In general, Python’s numeric types are straightforward, but a few coding concepts are worth highlighting here:

Integer and floating-point literals

Integers are written as a string of decimal digits. Floating-point numbers have an embedded decimal point, and/or an optional signed exponent introduced by an e or E. If you write a number with a decimal point or exponent, Python makes it a floating-point object and uses floating-point (not integer) math when it’s used in an expression. The rules for writing floating-point numbers are the same as in the C language.

Numeric precision and long integers

Plain Python integers (row 1 of Table 4-2) are implemented as C “longs” internally (i.e., at least 32 bits), and Python floating-point numbers are implemented as C “doubles”; Python numbers get as much precision as the C compiler used to build the Python interpreter gives to longs and doubles.^[2]

Long integer literals

On the other hand, if an integer literal ends with an l or L, it becomes a Python long integer (not to be confused with a C long) and can grow as large as needed. In Python 2.2, because integers are converted to long integers on overflow, the letter L is no longer strictly required.

H exadecimal and octal literals

The rules for writing hexadecimal (base 16) and octal (base 8) integers are the same as in C. Octal literals start with a leading zero (0), followed by a string of digits 0-7; hexadecimals start with a leading 0x or 0X, followed by hexadecimal digits 0-9, and A-F. In hexadecimal literals, hex digits may be coded in lower- or uppercase.

Complex numbers

Python complex literals are written as realpart+imaginarypart, where the imaginarypart is terminated with a j or J. The realpart is technically optional, and the imaginarypart can come first. Internally, they are implemented as a pair of floating-point numbers, but all numeric operations perform complex math when applied to complex numbers.

Built-in Tools and Extensions

Besides the built-in number literals shown in Table 4-2, Python provides a set of tools for processing number objects:

Expression operators

+, *, >>, **, etc.

Built-in mathematical functions

pow, abs, etc.

Utility modules

random, math, etc.

We’ll meet all of these as we go along. Finally, if you need to do serious number-crunching, an optional extension for Python called NumPy (Numeric Python) provides advanced numeric programming tools, such as a matrix data type and sophisticated computation libraries. Hardcore scientific programming groups at places like Lawrence Livermore and NASA use Python with NumPy to implement the sorts of tasks they previously coded in C++ or FORTRAN.

Because it’s so advanced, we won’t say more about NumPy in this chapter. (See the examples in Chapter 29.) You will find additional support for advanced numeric programming in Python at the Vaults of Parnassus site. Also note that NumPy is currently an optional extension; it doesn’t come with Python and must be installed separately.

Python Expression Operators

Perhaps the most fundamental tool that processes numbers is the expression: a combination of numbers (or other objects) and operators that computes a value when executed by Python. In Python, expressions are written using the usual mathematical notation and operator symbols. For instance, to add two numbers X and Y, say X+Y, which tells Python to apply the + operator to the values named by X and Y. The result of the expression is the sum of X and Y, another number object.

Table 4-3 lists all the operator expressions available in Python. Many are self-explanatory; for instance, the usual mathematical operators are supported: +, -, *, /, and so on. A few will be familiar if you’ve used C in the past: % computes a division remainder, << performs a bitwise left-shift, & computes a bitwise and result, etc. Others are more Python-specific, and not all are numeric in nature: the is operator tests object identity (i.e., address) equality, lambda creates unnamed functions, and so on. More on some of these later.

Table 4-3. Python expression operators and precedence

Operators	Description
lambda args: expression	Anonymous function generation
x or y	Logical or (y is evaluated only if x is false)
x and y	Logical and (y is evaluated only if x is true)
not x	Logical negation
x < y, x <= y, x > y, x >= y,x == y, x <> y, x != y,x is y, x is not y, x in y, x not in y	Comparison operators, value equality operators, object identity tests, and sequence membership
x | y	Bitwise or
x ^ y	Bitwise exclusive or
x & y	Bitwise and
x << y, x >> y	Shift x left or right by y bits
-x + y, x - y	Addition/concatenation, subtraction
x * y, x % y, x / y, x // y	Multiplication/repetition, remainder/format, division[3]
-x, +x, ~x, x ** y	Unary negation, identity, bitwise complement; binary power
x[i], x[i:j], x.attr, x(...)	Indexing, slicing, qualification, function calls
(...), [...], {...}, `...`	Tuple, list,[4] dictionary, conversion to string[5]
[3] Floor division (X // Y), new in 2.2, always truncates fractional remainders. This is further described in Section 4.5.3. [4] Beginning with Python 2.0, the list syntax ([...]) can represent either a list literal, or a list comprehension expression. The latter of these is a newer addition to Python, which performs an implied loop and collects expression results in a new list. Because they are often best understood in conjunction with functions, list comprehensions are postponed until Chapter 14. [5] Conversion of objects to their print strings can also be accomplished with the more readable str and repr built-in functions, which are described in Section 4.5.2.

Mixed Operators: Operator Precedence

As in most languages, more complex expressions are coded by stringing together the operator expressions in Table 4-3. For instance, the sum of two multiplications might be written as a mix of variables and operators:

A * B + C * D

So how does Python know which operator to perform first? The solution to this lies in operator precedence. When you write an expression with more than one operator, Python groups its parts according to what are called precedence rules, and this grouping determines the order in which expression parts are computed. In Table 4-3, operators lower in the table have higher precedence and so bind more tightly in mixed expressions.

For example, if you write X + Y * Z, Python evaluates the multiplication first (Y * Z), then adds that result to X, because * has higher precedence (is lower in the table) than +. Similarly, in this section’s original example, both multiplications (A * B and C * D) will happen before their results are added.

Parentheses Group Subexpressions

You can forget about precedence completely if you’re careful to group parts of expressions with parentheses. When you enclose subexpressions in parentheses, you override Python precedence rules; Python always evaluates expressions in parentheses first, before using their results in the enclosing expressions.

For instance, instead of coding X + Y * Z, write one of the following to force Python evaluate the expression in the desired order:

(X + Y) * Z
X + (Y * Z)

In the first case, + is applied to X and Y first, because it is wrapped in parentheses. In the second cases, the * is performed first (just as if there were no parentheses at all). Generally speaking, adding parentheses in big expressions is a great idea; it not only forces the evaluation order you want, but it also aids readability.

Mixed Types: Converted Up

Besides mixing operators in expressions, you can also mix numeric types. For instance, you can add an integer to a floating-point number:

40 + 3.14

But this leads to another question: what type is the result—integer or floating-point? The answer is simple, especially if you’ve used almost any other language before: in mixed type expressions, Python first converts operands up to the type of the most complicated operand, and then performs the math on same-type operands. If you’ve used C, you’ll find this similar to type conversions in that language.

Python ranks the complexity of numeric types like so: integers are simpler than long integers, which are simpler than floating-point numbers, which are simpler than complex numbers. So, when an integer is mixed with a floating-point, as in the example, the integer is converted up to a floating-point value first, and floating-point math yields the floating-point result. Similarly, any mixed-type expression where one operand is a complex number results in the other operand being converted up to a complex number that yields a complex result.

As you’ll see later in this section, as of Python 2.2, Python also automatically converts normal integers to long integers, whenever their values are too large to fit in a normal integer. Also keep in mind that all these mixed type conversions only apply when mixing numeric types around an operator or comparison (e.g., an integer and a floating-point number). In general, Python does not convert across other type boundaries. Adding a string to an integer, for example, results in an error, unless you manually convert one or the other; watch for an example when we meet strings in Chapter 5.

Preview: Operator Overloading

Although we’re focusing on built-in numbers right now, keep in mind that all Python operators may be overloaded (i.e., implemented) by Python classes and C extension types, to work on objects you create. For instance, you’ll see later that objects coded with classes may be added with + expressions, indexed with [i] expressions, and so on.

Furthermore, some operators are already overloaded by Python itself; they perform different actions depending on the type of built-in objects being processed. For example, the + operator performs addition when applied to numbers, but performs concatenation when applied to sequence objects such as strings and lists.^[6]

Numbers in Action

Probably the best way to understand numeric objects and expressions is to see them in action. So, start up the interactive command line and type some basic, but illustrative operations.

Basic Operations and Variables

First of all, let’s exercise some basic math. In the following interaction, we first assign two variables (a and b) to integers, so we can use them later in a larger expression. Variables are simply names—created by you or Python—that are used to keep track of information in your program. We’ll say more about this later, but in Python:

• Variables are created when first assigned a value.

• Variables are replaced with their values when used in expressions.

• Variables must be assigned before they can be used in expressions.

• Variables refer to objects, and are never declared ahead of time.

In other words, the assignments cause these variables to spring into existence automatically.

% python
>>> a = 3           # Name created
>>> b = 4

We’ve also used a comment here. In Python code, text after a # mark and continuing to the end of the line is considered to be a comment, and is ignored by Python. Comments are a place to write human-readable documentation for your code. Since code you type interactively is temporary, you won’t normally write comments there, but they are added to examples to help explain the code.^[7] In the next part of this book, we’ll meet a related feature—documentation strings—that attaches the text of your comments to objects.

Now, let’s use the integer objects in expressions. At this point, a and b are still 3 and 4, respectively; variables like these are replaced with their values whenever used inside an expression, and expression results are echoed back when working interactively:

                  >>> 
                  a + 1, a - 1        # Addition (3+1), subtraction (3-1)
(4, 2)

>>> 
                  b * 3, b / 2        # Multiplication (4*3), division (4/2)
(12, 2)

>>> 
                  a % 2, b ** 2       # Modulus (remainder), power 
(1, 16)

>>> 
                  2 + 4.0, 2.0 ** b   # Mixed-type conversions
(6.0, 16.0)

Technically, the results being echoed back here are tuples of two values, because lines typed at the prompt contain two expressions separated by commas; that’s why the result are displayed in parenthesis (more on tuples later). Notice that the expressions work because the variables a and b within them have been assigned values; if you use a different variable that has never been assigned, Python reports an error rather than filling in some default value:

>>> c * 2
Traceback (most recent call last):
  File "<stdin>", line 1, in ?
NameError: name 'c' is not defined

You don’t need to predeclare variables in Python, but they must be assigned at least once before you can use them at all. Here are two slightly larger expressions to illustrate operator grouping and more about conversions:

>>> b / 2 + a             # Same as ((4 / 2) + 3)
5
>>> print b / (2.0 + a)   # Same as (4 / (2.0 + 3))
0.8

In the first expression, there are no parentheses, so Python automatically groups the components according to its precedence rules—since / is lower in Table 4-3 than +, it binds more tightly, and so is evaluated first. The result is as if the expression had parenthesis as shown in the comment to the right of the code. Also notice that all the numbers are integers in the first expression; because of that, Python performs integer division and addition.

In the second expression, parentheses are added around the + part to force Python to evaluate it first (i.e., before the /). We also made one of the operands floating-point by adding a decimal point: 2.0. Because of the mixed types, Python converts the integer referenced by a to a floating-point value (3.0) before performing the +. It also converts b to a floating-point value (4.0) and performs a floating-point division; (4.0/5.0) yields a floating-point result of 0.8. If all the numbers in this expression were integers, it would invoke integer division (4/5), and the result would be the truncated integer 0 (in Python 2.2, at least—see the discussion of true division ahead).

Numeric Representation

By the way, notice that we used a print statement in the second example; without the print, you’ll see something that may look a bit odd at first glance:

>>> b / (2.0 + a)            # Auto echo output: more digits
0.80000000000000004

>>> print b / (2.0 + a)      # print rounds off digits.
0.8

The whole story behind this has to do with the limitations of floating-point hardware, and its inability to exactly represent some values. Since computer architecture is well beyond this book’s scope, though, we’ll finesse this by saying that all of the digits in the first output are really there, in your computer’s floating-point hardware; it’s just that you’re not normally accustomed to seeing them. We’re using this example to demonstrate the difference in output formatting—the interactive prompt’s automatic result echo shows more digits than the print statement. If you don’t want all the digits, say print.

Note that not all values have so many digits to display:

>>> 1 / 2.0
0.5

And there are more ways to display the bits of a number inside your computer than prints and automatic echoes:

>>> num = 1 / 3.0
>>> num                     # Echoes
0.33333333333333331
>>> print num               # Print rounds
0.333333333333

>>> "%e" % num              # String formatting
'3.333333e-001'
>>> "%2.2f" % num           # String formatting
'0.33'

The last two of these employ string formatting—an expression that allows for format flexibility, explored in the upcoming chapter on strings.

Str and Repr Display Formats

Technically, the difference between default interactive echoes and prints corresponds to the difference between the built-in repr and str functions:

>>> repr(num)               # Used by echoes: as code form
'0.33333333333333331'
>>> str(num)                # Used by print: user-friendly form
'0.333333333333'

Both of these convert arbitrary objects to their string representation: repr (and the interactive prompt) produces results that look as though they were code; str (and the print statement) converts to a typically more user-friendly format. This notion will resurface when we study strings; more on these built-ins in general later in the book.

Division: Classic, Floor, and True

Now that you’ve seen how division works, you should know that it is scheduled for a slight change in a future Python release (currently, in 3.0, scheduled to appear years after this edition is released). In Python 2.3, things work as just described, but there are actually two different division operators, one of which will change:

X / Y

Classic division. In Python 2.3 and earlier, this operator truncates results down for integers, and keeps remainders for floating-point numbers, as described here. This operator will be changed to true division—always keeping remainders regardless of types—in a future Python release (3.0).

X // Y

Floor division. Added in Python 2.2, this operator always truncates fractional remainders down to their floor, regardless of types.

Floor division was added to address the fact that the result of the current classic division model is dependent on operand types, and so can sometimes be difficult to anticipate in a dynamically-typed language like Python.

Due to possible backward compatibility issues, this is in a state of flux today. In version 2.3, / division works as described by default, and // floor division has been added to truncate result remainders to their floor regardless of types:

>>> (5 / 2), (5 / 2.0), (5 / -2.0), (5 / -2)
(2, 2.5, -2.5, -3)

>>> (5 // 2), (5 // 2.0), (5 // -2.0), (5 // -2)
(2, 2.0, -3.0, -3)

>>> (9 / 3), (9.0 / 3), (9 // 3), (9 // 3.0)
(3, 3.0, 3, 3.0)

In a future Python release, / division will likely be changed to return a true division result which always retains remainders, even for integers—for example, 1/2 will be 0.5, not 0, and 1//2 will still be 0.

Until this change is incorporated completely, you can see the way that the / will likely work in the future, by using a special import of the form: from __future__ import division. This turns the / operator into a true division (keeping remainders), but leaves // as is. Here’s how / will eventually behave:

>>> from __future__ import division

>>> (5 / 2), (5 / 2.0), (5 / -2.0), (5 / -2)
(2.5, 2.5, -2.5, -2.5)

>>> (5 // 2), (5 // 2.0), (5 // -2.0), (5 // -2)
(2, 2.0, -3.0, -3)

>>> (9 / 3), (9.0 / 3), (9 // 3), (9 // 3.0)
(3.0, 3.0, 3, 3.0)

Watch for a simple prime number while loop example in Chapter 10, and a corresponding exercise at the end of Part IV, which illustrate the sort of code that may be impacted by this / change. In general, any code that depends on / truncating an integer result may be effected (use the new // instead). As we write this, this change is scheduled to occur in Python 3.0, but be sure to try these expressions in your version to see which behavior applies. Also stay tuned for more on the special from command used here in Chapter 18.

B itwise Operations

Besides the normal numeric operations (addition, subtraction, and so on), Python supports most of the numeric expressions available in the C language. For instance, here it’s at work performing bitwise shift and Boolean operations:

>>> x = 1        # 0001
>>> x << 2       # Shift left 2 bits: 0100
4
>>> x | 2        # bitwise OR: 0011
3
>>> x & 1        # bitwise AND: 0001
1

In the first expression, a binary 1 (in base 2, 0001) is shifted left two slots to create a binary 4 (0100). The last two operations perform a binary or (0001|0010 = 0011), and a binary and (0001&0001 = 0001). Such bit masking operations allow us to encode multiple flags and other values within a single integer.

We won’t go into much more detail on “bit-twiddling” here. It’s supported if you need it, but be aware that it’s often not as important in a high-level language such as Python as it is in a low-level language such as C. As a rule of thumb, if you find yourself wanting to flip bits in Python, you should think about which language you’re really coding. In general, there are often better ways to encode information in Python than bit strings.^[8]

L ong Integers

Now for something more exotic: here’s a look at long integers in action. When an integer literal ends with a letter L (or lowercase l), Python creates a long integer. In Python, a long integer can be arbitrarily big—it can have as many digits as you have room for in memory:

>>> 9999999999999999999999999999999999999L + 1
10000000000000000000000000000000000000L

The L at the end of the digit string tells Python to create a long integer object with unlimited precision. As of Python 2.2, even the letter L is largely optional—Python automatically converts normal integers up to long integers, whenever they overflow normal integer precision (usually 32 bits):

>>> 9999999999999999999999999999999999999 + 1
10000000000000000000000000000000000000L

Long integers are a convenient built-in tool. For instance, you can use them to count the national debt in pennies in Python directly (if you are so inclined and have enough memory on your computer). They are also why we were able to raise 2 to such large powers in the examples of Chapter 3:

>>> 2L ** 200
1606938044258990275541962092341162602522202993782792835301376L
>>>
>>> 2 ** 200
1606938044258990275541962092341162602522202993782792835301376L

Because Python must do extra work to support their extended precision, long integer math is usually substantially slower than normal integer math (which usually maps directly to the hardware). If you need the precision, it’s built in for you to use; but there is a performance penalty.

A note on version skew: prior to Python 2.2, integers were not automatically converted up to long integers on overflow, so you really had to use the letter L to get the extended precision:

>>> 9999999999999999999999999999999999999 + 1         # Before 2.2
OverflowError: integer literal too large

>>> 9999999999999999999999999999999999999L + 1        # Before 2.2
10000000000000000000000000000000000000L

In Version 2.2 the L is mostly optional. In the future, it is possible that using the letter L may generate a warning. Because of that, you are probably best off letting Python convert up for you automatically when needed, and omitting the L.

Complex Numbers

C omplex numbers are a distinct core object type in Python. If you know what they are, you know why they are useful; if not, consider this section optional reading. Complex numbers are represented as two floating-point numbers—the real and imaginary parts—and are coded by adding a j or J suffix to the imaginary part. We can also write complex numbers with a nonzero real part by adding the two parts with a +. For example, the complex number with a real part of 2 and an imaginary part of -3 is written: 2 + -3j. Here are some examples of complex math at work:

>>> 1j * 1J
(-1+0j)
>>> 2 + 1j * 3
(2+3j)
>>> (2+1j)*3
(6+3j)

Complex numbers also allow us to extract their parts as attributes, support all the usual mathematical expressions, and may be processed with tools in the standard cmath module (the complex version of the standard math module). Complex numbers typically find roles in engineering-oriented programs. Since they are an advanced tool, check Python’s language reference manual for additional details.

Hexadecimal and Octal Notation

As mentioned at the start of this section, Python integers can be coded in hexadecimal (base 16) and octal (base 8) notation, in addition to the normal base 10 decimal coding:

• Octal literals have a leading 0, followed by a string of octal digits 0-7, each of which represents 3 bits.

• Hexadecimal literals have a leading 0x or 0X, followed by a string of hex digits 0-9 and upper- or lowercase A-F, each of which stands for 4 bits.

Keep in mind that this is simply an alternative syntax for specifying the value of an integer object. For example, the following octal and hexadecimal literals produce normal integers, with the specified values:

>>> 01, 010, 0100              # Octal literals
(1, 8, 64)
>>> 0x01, 0x10, 0xFF           # Hex literals
(1, 16, 255)

Here, the octal value 0100 is decimal 64, and hex 0xFF is decimal 255. Python prints in decimal by default, but provides built-in functions that allow you to convert integers to their octal and hexadecimal digit strings:

>>> oct(64), hex(64), hex(255)
('0100', '0x40', '0xff')

The oct function converts decimal to octal, and hex to hexadecimal. To go the other way, the built-in int function converts a string of digits to an integer; an optional second argument lets you specify the numeric base:

>>> int('0100'), int('0100', 8), int('0x40', 16)
(100, 64, 64)

The eval function, which you’ll meet later in this book, treats strings as though they were Python code. It therefore has a similar effect (but usually runs more slowly—it actually compiles and runs the string as a piece of a program):

>>> eval('100'), eval('0100'), eval('0x40')
(100, 64, 64)

Finally, you can also convert integers to octal and hexadecimal strings with a string formatting expression:

>>> "%o %x %X" % (64, 64, 255)
'100 40 FF'

This is covered in Chapter 4.

One warning before moving on, be careful to not begin a string of digits with a leading zero in Python, unless you really mean to code an octal value. Python will treat it as base 8, which may not work as you’d expect—010 is always decimal 8, not decimal 10 (despite what you might think!).

Other Numeric Tools

Python also provides both built-in functions and built-in modules for numeric processing. Here are examples of the built-in math module and a few built-in functions at work.

>>> import math
>>> math.pi, math.e
(3.1415926535897931, 2.7182818284590451)

>>> math.sin(2 * math.pi / 180)
0.034899496702500969

>>> abs(-42), 2**4, pow(2, 4)
(42, 16, 16)

>>> int(2.567), round(2.567), round(2.567, 2)
(2, 3.0, 2.5699999999999998)

The math module contains most of the tools in the C language’s math library. As described earlier, the last output here will be just 2.57 if we say print.

Notice that built-in modules such as math must be imported, but built-in functions such as abs are always available without imports. In other words, modules are external components, but built-in functions live in an implied namespace, which Python automatically searches to find names used in your program. This namespace corresponds to the module called __builtin__. There is much more about name resolution in Part IV, Functions; for now, when you hear “module,” think “import.”

The Dynamic Typing Interlude

If you have a background in compiled or statically-typed languages like C, C++, or Java, you might find yourself in a perplexed place at this point. So far, we’ve been using variables without declaring their types—and it somehow works. When we type a = 3 in an interactive session or program file, how does Python know that a should stand for an integer? For that matter, how does Python know what a even is at all?

Once you start asking such questions, you’ve crossed over into the domain of Python’s dynamic typing model. In Python, types are determined automatically at runtime, not in response to declarations in your code. To you, it means that you never declare variables ahead of time, and that is perhaps a simpler concept if you have not programmed in other languages before. Since this is probably the most central concept of the language, though, let’s explore it in detail here.

How Assignments Work

You’ll notice that when we say a = 3, it works, even though we never told Python to use name a as a variable. In addition, the assignment of 3 to a seems to work too, even though we didn’t tell Python that a should stand for an integer type object. In the Python language, this all pans out in a very natural way, as follows:

Creation

A variable, like a, is created when it is first assigned a value by your code. Future assignments change the already-created name to have a new value. Technically, Python detects some names before your code runs; but conceptually, you can think of it as though assignments make variables.

Types

A variable, like a, never has any type information or constraint associated with it. Rather, the notion of type lives with objects, not names. Variables always simply refer to a particular object, at a particular point in time.

Use

When a variable appears in an expression, it is immediately replaced with the object that it currently refers to, whatever that may be. Further, all variables must be explicitly assigned before they can be used; use of unassigned variables results in an error.

This model is strikingly different from traditional languages, and is responsible for much of Python’s conciseness and flexibility. When you are first starting out, dynamic typing is usually easier to understand if you keep clear the distinction between names and objects. For example, when we say this:

>>> a = 3

At least conceptually, Python will perform three distinct steps to carry out the request, which reflect the operation of all assignments in the Python language:

1. Create an object to represent the value 3.

2. Create the variable a, if it does not yet exist.

3. Link the variable a to the new object 3.

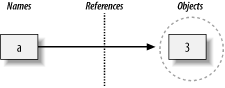
The net result will be a structure inside Python that resembles Figure 4-1. As sketched, variables and objects are stored in different parts of memory, and associated by links—shown as a pointer in the figure. Variables always link to objects (never to other variables), but larger objects may link to other objects.

Figure 4-1. Names and objects, after a = 3

These links from variables to objects are called references in Python—a kind of association.^[9] Whenever variables are later used (i.e., referenced), the variable-to-object links are automatically followed by Python. This is all simpler than its terminology may imply. In concrete terms:

• Variables are simply entries in a search table, with space for a link to an object.

• Objects are just pieces of allocated memory, with enough space to represent the value they stand for, and type tag information.

At least conceptually, each time you generate a new value in your script, Python creates a new object (i.e., a chunk of memory) to represent that value. Python caches and reuses certain kinds of unchangeable objects like small integers and strings as an optimization (each zero is not really a new piece of memory); but it works as though each value is a distinct object. We’ll revisit this concept when we meet the == and is comparisons in Section 7.6 in Chapter 7.

Let’s extend the session and watch what happens to its names and objects:

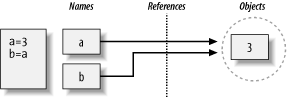
>>> a = 3
>>> b = a

After typing these two statements, we generate the scene captured in Figure 4-2. As before, the second line causes Python to create variable b; variable a is being used and not assigned here, so it is replaced with the object it references (3); and b is made to reference that object. The net effect is that variables a and b wind up referencing the same object (that is, pointing to the same chunk of memory). This is called a shared reference in Python—multiple names referencing the same object.

Figure 4-2. Names and objects, after b = a

Next, suppose we extend the session with one more statement:

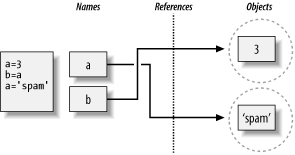
>>> a = 3
>>> b = a
>>> a = 'spam'

As for all Python assignments, this simply makes a new object to represent the string value “spam”, and sets a to reference this new object. It does not, however, change the value of b; b still refers to the original object, the integer 3. The resulting reference structure is as in Figure 4-3.

Figure 4-3. Names and objects, after a = `spam’

The same sort of thing would happen if we changed b to “spam” instead—the assignment would only change b, and not a. This example tends to look especially odd to ex-C programmers—it seems as though the type of a changed from integer to string, by saying a = 'spam‘. But not really. In Python, things work more simply: types live with objects, not names. We simply change a to reference a different object.

This behavior also occurs if there are no type differences at all. For example, consider these three statements:

>>> a = 3
>>> b = a
>>> a = 5

In this sequence, the same events transpire: Python makes variable a reference the object 3, and makes b reference the same object as a, as in Figure 4-2. As before, the last assignment only sets a to a completely different object, integer 5. It does not change b as a side effect. In fact, there is no way to ever overwrite the value of object 3 (integers can never be changed in place—a property called immutability). Unlike some languages, Python variables are always pointers to objects, not labels of changeable memory areas.

References and Changeable Objects

As you’ll see later in this part’s chapters, though, there are objects and operations that perform in-place object changes. For instance, assignment to offsets in lists actually changes the list object itself (in-place), rather than generating a brand new object. For objects that support such in-place changes, you need to be more aware of shared references, since a change from one name may impact others. For instance, list objects support in-place assignment to positions:

>>> L1 = [2,3,4]
>>> L2 = L1

As noted at the start of this chapter, lists are simply collections of other objects, coded in square brackets; L1 here is a list containing objects 2, 3, and 4. Items inside a list are accessed by their positions; L1[0] refers to object 2, the first item in the list L1.

Lists are also objects in their own right, just like integers and strings. After running the two prior assignments, L1 and L2 reference the same object, just like the prior example (see Figure 4-2). Also as before, if we now say this:

>>> L1 = 24

then L1 is simply set to a different object; L2 is still the original list. If instead we change this statement’s syntax slightly, however, it has radically different effect:

>>> L1[0] = 24
>>> L2
[24, 3, 4]

Here, we’ve changed a component of the object that L1 references, rather than changing L1 itself. This sort of change overwrites part of the list object in-place. The upshot is that the effect shows up in L2 as well, because it shares the same object as L1.

This is usually what you want, but you should be aware of how this works so that it’s expected. It’s also just the default: if you don’t want such behavior, you can request that Python copy objects, instead of making references. We’ll explore lists in more depth, and revisit the concept of shared references and copies, in Chapter 6 and Chapter 7.^[10]

References and Garbage Collection

When names are made to reference new objects, Python also reclaims the old object, if it is not reference by any other name (or object). This automatic reclamation of objects’ space is known as garbage collection . This means that you can use objects liberally, without ever needing to free up space in your script. In practice, it eliminates a substantial amount of bookkeeping code compared to lower-level languages such as C and C++.

To illustrate, consider the following example, which sets name x to a different object on each assignment. First of all, notice how the name x is set to a different type of object each time. It’s as though the type of x is changing over time; but not really, in Python, types live with objects, not names. Because names are just generic references to objects, this sort of code works naturally:

>>> x = 42
>>> x = 'shrubbery'     # Reclaim 42 now (?)
>>> x = 3.1415          # Reclaim 'shrubbery' now (?)
>>> x = [1,2,3]         # Reclaim 3.1415 now (?)

Second of all, notice that references to objects are discarded along the way. Each time x is assigned to a new object, Python reclaims the prior object. For instance, when x is assigned the string 'shrubbery', the object 42 will be immediately reclaimed, as long as it is not referenced anywhere else—the object’s space is automatically thrown back into the free space pool, to be reused for a future object.

Technically, this collection behavior may be more conceptual than literal, for certain types. Because Python caches and reuses integers and small strings as mentioned earlier, the object 42 is probably not literally reclaimed; it remains to be reused the next time you generate a 42 in your code. Most kinds of objects, though, are reclaimed immediately when no longer referenced; for those that are not, the caching mechanism is irrelevant to your code.

Of course, you don’t really need to draw name/object diagrams with circles and arrows in order to use Python. When you are starting out, though, it sometimes helps you understand some unusual cases, if you can trace their reference structure. Moreover, because everything seems to be assignment and references in Python, a basic understanding of this model helps in many contexts—as we’ll see, it works the same in assignment statements, for loop variables, function arguments, module imports, and more.

---

^[1] In this book, the term literal simply means an expression whose syntax generates an object—sometimes also called a constant. If you hear these called constants, it does not imply objects or variables that can never be changed (i.e., this is unrelated to C++’s const, or Python’s “immutable”—a topic explored later in this part of the book).

^[2] That is, the standard CPython implementation. In the Jython Java-based implementation, Python types are really Java classes.

^[6] This is usually called polymorphism—the meaning of an operation depends on the type of objects being operated on. We’ll revisit this word when we explore functions in Chapter 12, because it becomes a much more obvious feature there.

^[7] If you’re working along, you don’t need to type any of the comment text from # through the end of the line; comments are simply ignored by Python, and not a required part of the statements we run.

^[8] As for most rules, there are exceptions. For instance, if you interface with C libraries that expect bit strings to be passed in, this doesn’t apply.

^[9] Readers with a background in C may find Python references similar to C pointers (memory addresses). In fact, references are implemented as pointers, and often serve the same roles, especially with objects that can be changed in place (more on this later). However, because references are always automatically dereferenced when used, you can never actually do anything useful with a reference itself; this is a feature, which eliminates a vast category of C bugs. But, you can think of Python references as C “void*” pointers, which are automatically followed whenever used.

^[10] Objects that can be changed in-place are known as mutables—lists and dictionaries are mutable built-ins, and hence susceptible to in-place change side-effects.