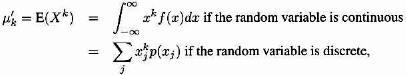Loss Models: From Data to Decisions, 4th Edition

3.1 Moments

There are a variety of interesting calculations that can be done from the models described in Chapter 2. Examples are the average amount paid on a claim that is subject to a deductible or policy limit or the average remaining lifetime of a person age 40.

Definition 3.1 The kth raw moment of a random variable is the expected (average) value of the kth power of the variable, provided it exists. It is denoted by E(X^k) or by μ′_k. The first raw moment is called the mean of the random variable and is usually denoted by μ.

Note that μ is not related to μ(x), the force of mortality from Definition 2.7. For random variables that take on only nonnegative values [i.e., Pr(X ≥ 0) = 1], k may be any real number. When presenting formulas for calculating this quantity, a distinction between continuous and discrete variables needs to be made. Formulas will be presented for random variables that are either everywhere continuous or everywhere discrete. For mixed models, evaluate the formula by integrating with respect to its density function wherever the random variable is continuous and by summing with respect to its probability function wherever the random variable is discrete and adding the results. The formula for the kth raw moment is

(3.1)

where the sum is to be taken over all x_j with positive probability. Finally, note that it is possible that the integral or sum will not converge, ...