Loss Models: From Data to Decisions, 4th Edition

7.1 Compound frequency distributions

A larger class of distributions can be created by the processes of compounding any two discrete distributions. The term compounding reflects the idea that the pgf of the new distribution P_S(z) is written as

(7.1)

where P_N(z) and P_M(Z) are called the primary and secondary distributions, respectively.

The compound distributions arise naturally as follows. Let N be a counting random variable with pgf P_N(z). Let M₁, M₂, … be i.i.d. counting random variables with pgf P_M(Z). Assuming that the M_js do not depend on N, the pgf of the random sum S = M₁ + M₂ + ··· + M_N (where N = 0 implies that S = 0) is P_S(z) = P_N[P_M(z)]. This is shown as

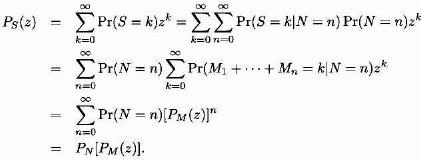
In insurance contexts, this distribution can arise naturally. If N represents the number of accidents arising in a portfolio of risks and {M_k : k = 1, 2, …, N} represents the number of claims (injuries, number of cars, etc.) from the accidents, then S represents the total number of claims from the portfolio. This kind of interpretation is not necessary to justify the use of a compound distribution. If a compound distribution fits data well, that may be enough justification itself. Also, there are other motivations for these distributions, as presented in Section 7.18.

EXAMPLE 7.1

Demonstrate that any zero-modified distribution ...