Machine Learning

Classification

In this case, a typical choice is to project on the half-space, Section 8.6.2, formed by the hyperplane

$y_n〈f_{n-1},\kappa (\cdot ,{\mathit{x}}_n)〉=\rho ,$

and the corresponding projection operator becomes

$P_k(f_{n-1})=f_{n-1}+{\beta }_k\kappa (\cdot ,{\mathit{x}}_k),$

where

$\begin{array}{l}\hfill {\beta }_k=\left\{\begin{array}{ll}\frac{\rho -y_k\langle f_{n-1},\kappa (\cdot ,{\mathit{x}}_k)\rangle }{\kappa ({\mathit{x}}_k,{\mathit{x}}_k)},& \text{if}\rho -y_k〈f_{n-1},\kappa (\cdot ,{\mathit{x}}_k)〉>0,\\ 0,& \text{otherwise}.\end{array}\right.\end{array}$

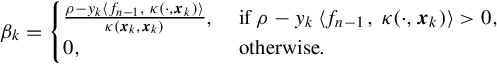  (11.110)

Recall that the corresponding half-space is the 0-level set of the hinge loss function, _ρ(y_n,f(x_n)) defined in (11.59).

Thus, for both cases, regression ...