Mastering Algorithms with C

Implementation and Analysis of Binary Search Trees

As described earlier, binary search trees perform well only if the tree remains balanced. Unfortunately, keeping a binary search tree balanced is a more difficult problem than it may at first appear. Nevertheless, there are a few clever approaches one can take. One of the best approaches is to implement the tree as an AVL tree.

An AVL (Adel’son-Vel’skii and Landis) tree is a special type of binary tree that stores an extra piece of information with each node: its balance factor . The balance factor of a node is the height of the subtree rooted at its left child minus the height of the subtree rooted at its right child (see Figure 9.9). As nodes are inserted, an AVL tree adjusts itself so that all balance factors stay +1, -1, or 0. A subtree whose root node has a balance factor of +1 is said to be left-heavy. A subtree whose root node has a balance factor of -1 is said to be right-heavy. A subtree whose root node has a balance factor of is considered balanced. By keeping its subtrees nearly balanced, an AVL tree stays approximately balanced overall.

Figure 9.9. An AVL tree, including balance factors

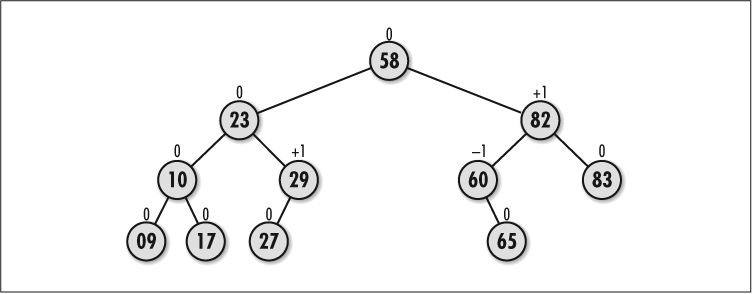
The basic means of searching and inserting nodes in an AVL tree is the same as described earlier. However, when we insert a node into an AVL tree, we have some additional work to do after the node descends to its appropriate position. First, ...