Mastering Algorithms with C

Description of Graphs

Graphs are composed of two types of elements: vertices and edges. Vertices represent objects, and edges establish relationships or connections between the objects. In many problems, values, or weights, are associated with a graph’s edges; however, such problems will not be considered further until Chapter 16.

Graphs may be either directed or undirected . In a directed graph, edges go from one vertex to another in a specific direction. Pictorially, a directed graph is drawn with circles for its vertices and arrows for its edges (see Figure 11.1a). Sometimes the edges of a directed graph are referred to as arcs . In an undirected graph, edges have no direction; thus, its edges are depicted using lines instead of arrows (see Figure 11.1b).

Figure 11.1. Two graphs: (a) a directed graph and (b) an undirected graph

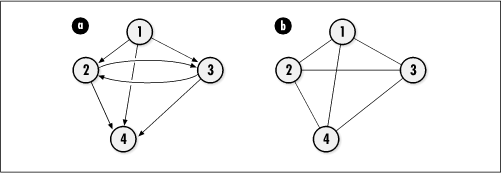
Formally, a graph is a pair G = (V, E ), where V is a set of vertices and E is a binary relation on V. In a directed graph, if an edge goes from vertex u to vertex v, E contains the ordered pair (u, v). For example, in Figure 11.1a, V = {1, 2, 3, 4} and E = {(1, 2), (1, 3), (1, 4), (2, 3), (2, 4), (3, 2), (3, 4)}. By convention, parentheses are used instead of braces for sets that represent edges in a graph. In an undirected graph, because an edge (u, v) is the same as (v, u), either edge is listed in E, but not both. Thus, in Figure 11.1b, V = {1, 2, 3, ...