Mastering Algorithms with C

Graph Example: Counting Network Hops

Graphs play an important part in solving many networking problems. One problem, for example, is determining the best way to get from one node to another in an internet, a network of gateways into other networks. One way to model an internet is using an undirected graph in which vertices represent nodes, and edges represent connections between the nodes. With this model, we can use breadth-first search to help determine the smallest number of traversals, or hops, between various nodes.

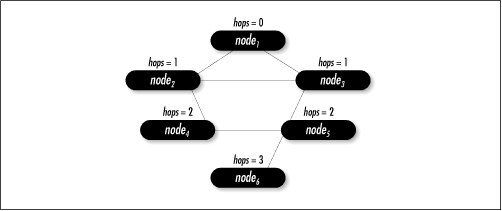
For example, consider the graph in Figure 11.8, which represents an internet of six nodes. Starting at node₁ , there is more than one way we can reach node₄ . The paths 〈 node₁ , node₂ , node₄ 〉, 〈 node₁ , node₃ , node₂ , node₄ 〉, and 〈 node₁ , node₃ , node5, node₄ 〉 are all acceptable. Breadth-first search determines the shortest path, 〈 node₁ , node₂ , node₄ 〉, which requires two hops.

Figure 11.8. Hop counts after performing a breadth-first search on an internet of six nodes

This example presents a function, bfs (see Examples Example 11.3 and Example 11.4), that implements breadth-first search. It is used here to determine the smallest number of hops between nodes in an internet. The function has three arguments: graph is a graph, which in this problem represents the internet; start is the vertex representing the starting point; and hops is the list of hop ...