Mastering Algorithms with C

Implementation and Analysis of Counting Sort

Counting sort works fundamentally by counting how many times integer elements occur in an unsorted set to determine how the set should be ordered. In the implementation presented here, data initially contains the unsorted set of size integer elements stored in a single block of contiguous storage. Additional storage is allocated to store the sorted data temporarily. Before ctsort returns, the sorted set is copied back into data.

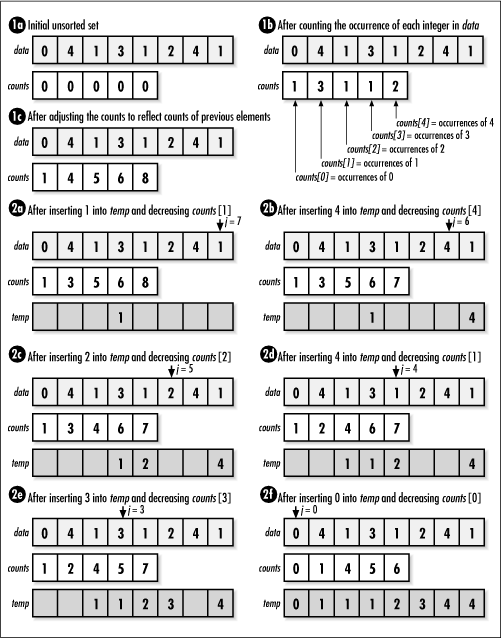
After allocating storage, we begin by counting the occurrences of each element in data (see Example 12.6). These are placed in an array of counts, counts, indexed by the integer elements themselves (see Figure 12.6, step 1b). Once the occurrences of each element in data have been counted, we adjust the counts to reflect the number of elements that will come before each element in the sorted set. We do this by adding the count of each element in the array to the count of the element that follows it (see Figure 12.6, step 1c). Effectively, counts then contains the offsets at which each element belongs in the sorted set, temp.

To complete the sort, we place each element in temp at its designated offset (see Figure 12.6, steps 2a- f ). The count for each element is decreased by 1 as temp is updated so that integers appearing more than once in data appear more than once in temp as well.

Figure 12.6. Sorting with counting ...