Mastering Algorithms with C

Implementation and Analysis of Radix Sort

Radix sort works fundamentally by applying counting sort one position at a time to a set of data. In the implementation presented here, data initially contains the unsorted set of size integer elements stored in a single block of contiguous storage. When rxsort returns, data is completely sorted.

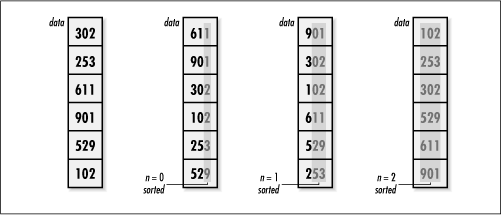
If we understand counting sort, the operation of radix sort is simple. A single loop governs the position on which we are currently sorting (see Example 12.7). Position by position, we apply counting sort to shuffle and reshuffle the elements, beginning with the least significant position. Once we have shuffled the elements by the digits in the most significant position, sorting is complete (see Figure 12.7). A simple approach involving exponentiation and modular arithmetic is used to obtain each digit value. This works well for integers. Different types of data require different approaches. Some approaches may require considering machine-specific details, such as byte ordering and word alignment.

Figure 12.7. Sorting integers as radix-10 numbers with radix sort

Not surprisingly, the runtime complexity of radix sort depends on the stable sorting algorithm chosen to sort the digits. Because radix sort applies counting sort once for each of the p positions of digits in the data, radix sort runs in p times the runtime complexity of counting sort, or O