Mastering Algorithms with C

Implementation and Analysis of Binary Search

Binary search works fundamentally by dividing a sorted set of data repeatedly and inspecting the element in the middle of each division. In the implementation presented here, the sorted set of data resides in sorted, a single block of contiguous storage. The argument target is the data we are searching for.

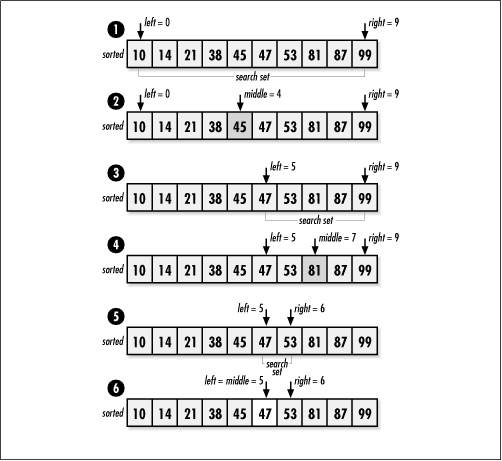
This implementation revolves around a single loop controlled by the variables left and right, which define the boundaries of the current set in which we are focusing our search (see Example 12.8). Initially, we set left and right to and size - 1, respectively. During each iteration of the loop, we set middle to the middle element of the set defined by left and right. If the element at middle is less than the target, we move the left index to one element after middle. Thus, the next set searched is the upper half of the current set. If the element at middle is greater than the target, we move the right index to one element before middle. Thus, the next set searched is the lower half of the current set. As the search continues, left moves from left to right, and right moves from right to left. The search terminates once we encounter the target at middle, or when left and right cross, if the target is not found. Figure 12.8 illustrates this process.

Figure 12.8. Searching for 47 using binary search

The runtime complexity of binary search depends ...