Description of Polynomial Interpolation
There are many problems that can be described in terms of a function. However, often this function is not known, and we must infer what we can about it from only a small number of points. To do this, we interpolate between the points. For example, in Figure 13.1, the known points along f (x) are x 0, . . ., x 8, shown by circular black dots. Interpolation helps us get a good idea of the value of the function at points z 0, z 1, and z 2, shown by white squares. This section presents polynomial interpolation.
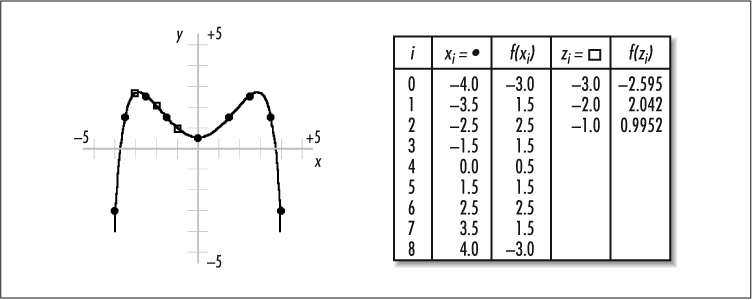
Fundamental to polynomial interpolation is the construction of a special polynomial called an interpolating polynomial. To appreciate the significance of this polynomial, let’s look at some principles of polynomials in general. First, a polynomial is a function of the form:
p(x) = a 0+a 1 x+a 2 x 2+. . . +a n x n
where a 0, . . ., an are coefficients. Polynomials of this form are said to have degree n, provided an is nonzero. This is the power form of a polynomial, which is especially common in mathematical discussions. However, other forms of polynomials are more convenient in certain contexts. For example, a form particularly relevant to polynomial interpolation is the Newton form:
p(x) = a 0+a 1(x-c 1)+a 2(x-c 1)(x-c 2)+ . . . +a n(x-c 1)( ...
Get Mastering Algorithms with C now with the O’Reilly learning platform.
O’Reilly members experience books, live events, courses curated by job role, and more from O’Reilly and nearly 200 top publishers.

