Mastering Algorithms with C

Description of Testing Whether Line Segments Intersect

One fundamental problem in computational geometry is determining whether two line segments intersect. Line segments are lines that have a beginning and an end. The points that define either end are a line segment’s endpoints . To determine whether two line segments intersect, we first need to understand a little about lines and line segments in general.

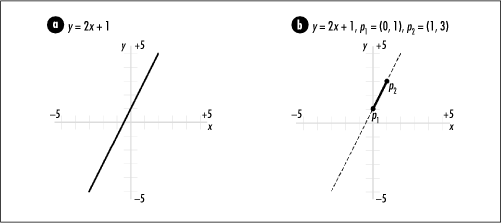
One representation of a line is point-intercept form , or y = mx + b, where m is the line’s slope and b is where the line crosses the y-axis. Using this, for any value of x, we can compute a corresponding value for y (see Figure 17.1a). For a line segment with endpoints p ₁ = (x ₁, y ₁) and p ₂ = (x ₂, y ₂), the slope m and y-intercept b are calculated by applying the following formulas:

Using m and b, the line segment is represented as a line in point-intercept form with endpoints p ₁ and p ₂ understood (see Figure 17.1b).

Figure 17.1. (a) A line and (b) a line segment with endpoints p₁ and p₂

Standard Test for Intersecting Line Segments

One way to determine whether two line segments intersect is first to determine the intersection point p_i = (x_i , y _i ) of the two lines on which each segment lies, then determine whether p_i is on both segments. If p_i is on both segments, the ...