Mastering Algorithms with C

Description of Convex Hulls

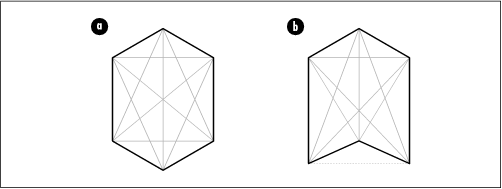
The convex hull of a set of points is the smallest convex polygon that encloses all points in the set. A polygon is convex if any line segment connecting two points inside the polygon lies completely inside the polygon itself (see Figure 17.3a); otherwise, the polygon is concave (see Figure 17.3b). To picture the convex hull for a set of points, imagine a series of pegs on a board. If we wrap a string tightly around the outermost pegs, the shape of the string is the convex hull.

Figure 17.3. (a) A convex polygon and (b) a concave polygon

Jarvis’s March

One way to construct the convex hull for a set of points P is to use a method called Jarvis’s march. Jarvis’s march constructs a convex hull in two sections, called the right chain and left chain. The right chain consists of all points in the convex hull from the lowest point (the one with the smallest y-coordinate) to the highest. If two points are equally low, the lowest point is considered to be the one that is also the furthest to the left (the one with the smallest x-coordinate). The left chain consists of all points from the highest point back to the lowest. If two points are equally high, the highest point is considered to be the one that is also the furthest to the right.

We begin by finding the lowest point in P (as described a moment ago), adding it to the convex hull, and initializing another ...