Mastering Algorithms with C

Description of Arc Length on Spherical Surfaces

Many problems require computing the distance between two points. When we are interested in the distance between points along a straight line, we apply the well-known distance formula derived from the Pythagorean theorem. However, if we are interested in the distance between points along a curved surface, the problem becomes more difficult. Fortunately, computing the minimum distance, or arc length, between two points on a spherical surface is a special case that is relatively simple. To begin, let’s look at two different coordinate systems, rectilinear coordinates and spherical coordinates.

Rectilinear and Spherical Coordinates

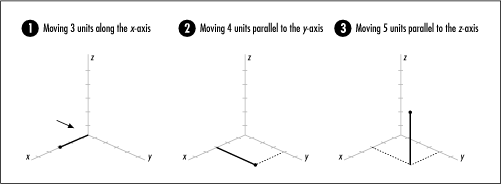
The rectilinear coordinate system is the coordinate system that is most familiar to us. In rectilinear coordinates, a point’s location is specified using three values, x, y, z, which are its positions along the x-axis, y-axis, and z-axis. Referring to Figure 17.5, the z-axis is positive going upward. Standing at the arrow looking forward, the x-axis is positive to the right, and the y-axis is positive straight ahead. From this vantage point, the positive directions for x and y look the same as in two dimensions. Thus, to locate (3, 4, 5), for example, we move three units to the right along the x-axis, four units ahead parallel to the y-axis, and five units up parallel to the z-axis (see Figure 17.5).

Figure 17.5. Locating ...