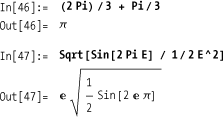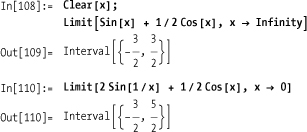Chapter 1. Numerics
Jenny I’ve got your number I need to make you mine Jenny don’t change your number Eight six seven five three oh nine Eight six seven five three oh nine Eight six seven five three oh nine Eight six seven five three oh nine
—Tommy Tutone, “867-5309/Jenny”
1.0 Introduction
Numerical Types
Mathematics is a huge, almost all-encompassing subject, and the average layperson often fails to appreciate the types of exotic objects that are in the mathematician’s domain. Yet every person on the street perceives math is about numbers. So even though numbers only scratch the surface of math and Mathematica, it makes sense to begin with their representation.
Mathematica supports four numerical types: Integer, Rational, Real, and Complex. In the following examples we use
Mathematica’s comment notation ( *comment* ).
1 (*The integer one*) 1 / 2 (*The rational one half*) 1.2 * ^ 8 (*The real 1.2 x 10^8*) 3 + 2 I (*The complex number 3+2i*)
There is no need to take my word that these expressions have the
specified types. You can ask Mathematica to tell you using the
function Head[] , which returns the head
of an expression (i.e., head of a list).
In[2]:= Head[1] Out[2]= Integer In[3]:= Head[1/2] Out[3]= Rational In[4]:= Head[1.2 ^ 8] Out[4]= Real In[5]:= Head[3 + 2 I] Out[5]= Complex
Although Mathematica does not internally store numbers
as lists, it provides the illusion that a number has a head indicating
its type. This is consistent with the fact that everything in
Mathematica is an expression and every expression must have a head. It
is also common for Mathematica to use the head to indicate type when
constructing more complex objects. See 1.5 Working with Intervals, for example. If you are confused
by this, for now, just think of Head as returning a type name when presented
with an atomic expression (expressions that can’t
be divided into subexpressions).
Exact and Approximate Results
Mathematica is unique in comparison to most mathematical tools and programming languages in that it will usually produce exact results unless you tell it otherwise. The following examples show the difference between exact and approximate results. 1.1 Controlling Precision and Accuracy and 1.2 Mixing Different Numerical Types show you how to make Mathematica use the appropriate form.
Exact results are displayed in their entirety when possible or symbolically when full display would be impossible due to the infinity of the exact representation.
Approximate numeric results are represented in machine precision floating point by default. On most modern computers, this means double-precision floating-point numbers, which contain a total of 64 binary bits, typically yielding 16 decimal digits of mantissa. You can also specify numbers with greater than machine precision (see 1.1 Controlling Precision and Accuracy) but there is a performance cost: Mathematica must switch from the native hardware-based floating-point algorithms to software-based ones.
In[8]:= 3. ^ 1000 Out[8]= 1.322070819480807 x 10477 In[9]:= Sqrt[2.] Out[9]= 1.41421
By adding a decimal point to a number, you force Mathematica to treat it as approximate. These approximate numbers will be machine precision by default, but there are several ways to force higher precision. 1.1 Controlling Precision and Accuracy and 1.2 Mixing Different Numerical Types in this chapter will elaborate on these differences.
Numerical Expressions
The previous examples show simple numerical expressions. In
practice, Mathematica follows general mathematical notation, but in
many cases this means that there are multiple ways to express the same
thing. Let’s consider each of the common operations that arise in
algebra. There are several ways to express multiplication, division,
and other arithmetic operations. A single space between expressions
(e.g., variables, numbers) implies multiplication, as is the typical
convention among mathematicians. You can evaluate typeset mathematics
using special symbols, such as ×. You can also use Full
Form (e.g., Plus,
Times, Divide), but for arithmetic this is
unnecessarily verbose.
The various representations are known as “forms” in
Mathematica (e.g., InputForm,
OutputForm, TraditionalForm, etc.). 1.7 Displaying Numbers in Alternate Forms shows you how to
control what form is used for output of results. Controlling what form
is used for input is a function of using the various features of the
Mathematica frontend (palettes, shortcut keys, etc.). This book will
not discuss the use of the frontend, since its main focus is
programming, and there are numerous other resources (the best being
the integrated help system) for mastering the frontend.
Numerical Approximations
Mathematica is famous for its symbolic abilities; however, when
it comes to numerical methods it is also no slouch! The core functions
for numerical solutions are NSum,
NProduct, NSolve, NIntegrate, and NDSolve. These are covered in Chapter 10 and Chapter 12.
1.1 Controlling Precision and Accuracy
Problem
You want numerical results that are to a specified numerical precision and accuracy.
Solution
Use N[] to convert from exact
to approximate form while controlling precision and accuracy to the
desired amount.
In[19]:= N[1/5]
Out[19]= 0.2You can explicitly specify the precision as a second
argument to N[].
In[20]:= N[1/17,10]
Out[20]= 0.05882352941You can also explicitly specify both the precision and accuracy, but this is less common. You might do this to guarantee a fixed number of decimal places independent of the size of the actual number.
In[21]:= N[{17, 1/17}, {Infinity, 10}]
Out[21]= {17.000000000, 0.0588235294}To drive this point home, I ask you to consider the following. The first column uses fixed precision, whereas the second uses infinite precision and fixed accuracy.
In[22]:= Table[With [{x = 10^n + 1 /17}, {N[x, 10], N[x, {Infinity, 10}]}], {n, 0, 5}] // TableForm Out[22]//TableForm= 1.058823529 1.058823529 10.05882353 10.058823529 100.0588235 100.058823529 1000.058824 1000.058823529 10000.05882 10000.0588235294 100000.0588 100000.0588235294
Discussion
For most purposes, treat precision as the total number of digits in the decimal representation of a number and accuracy as the total number of digits after the decimal. As such, precision is a measure of relative uncertainty (given a precision p a larger number will have more uncertainty than a smaller number). Accuracy is an absolute measure of uncertainty because the number of places after the decimal is independent of the magnitude of the number. Typically you only need to control precision in most applications.
There are two common syntaxes for using N[]. You already saw the functional syntax
in the solution section. The second uses Mathematica’s postfix
notation. See the sidebar Mathematica Expressions
for a discussion of postfix and other notations.
In[29]:= Sqrt[2] //N
Out[29]= 1.41421It is common to use this notation to force Mathematica to convert an exact or symbolic result to an approximate result as the last step in a computation. When you use postfix notation, you can explicitly specify the precision, but it is a bit awkward.
In[30]:= Sqrt[2] //N[#, 10]&
Out[30]= 1.414213562When you don’t specify precision, Mathematica uses MachinePrecision, which is a built-in symbol
that denotes the precision native to your computer’s floating-point
capabilities. The numerical value of MachinePrecision is stored in a variable
$MachinePrecision.
In[31]:= $MachinePrecision
Out[31]= 15.9546There is another notation that is less common but you may come
across it in Mathematica output. If a literal number is displayed with
a trailing ` (backtick) followed
optionally by a number, this indicates the number is either in machine
precision or is in the precision specified by the number following the
backtick.
In[32]:= 20` (*20 in machine precision*) Out[32]= 20. In[33]:= 20`20 (*20 with high precision of 20 digits*) Out[33]= 20.000000000000000000
In a complex expression with a lot of high-precision numbers,
you can avoid specifying each precision individually by using SetPrecision[].
In[34]:= SetPrecision[20. + 1/3 * 12.3 / 37.8 + Pi, 20] (*All numbers will be set to a precision of 20.*) Out[34]= 23.250058262055400604
Note
You may find it surprising that $MachinePrecision is not an integer. The
reason stems from the formal definition of
precision, which is derived from considering a
number x
and its uncertainty dx
and using the expression -
Log[10, dx/x]. Accuracy is defined as - Log[10, dx].
If you have an expression and need to know the precision or accuracy, you can use the following functions.
In[35]:= Precision[2.] Out[35]= MachinePrecision In[36]:= Precision[2'20] Out[36]= 20.
Exact results have infinite precision.
In[37]:= Precision[Sqrt[2]] Out[37]= ∞ In[38]:= Precision[Sqrt[2.]] Out[38]= MachinePrecision In[39]:= Accuracy[2.] Out[39]= 15.6536
You are not guaranteed the accuracy you specify if the precision is too small.
In[40]:= Accuracy[N[30, {20, 20}]]
Out[40]= 18.5229With enough precision, however, you will get accuracy.
In[41]:= Accuracy[N[30, {30, 20}]]
Out[41]= 20.And precision can even be specified as infinite!
In[42]:= Accuracy[N[30, {Infinity, 20}]]
Out[42]= 20.Mathematica also defines two internal variables: $MinPrecision, whose default value is zero,
and $MaxPrecision, whose default
value is plus infinity.
In[43]:= {$MinPrecision, $MaxPrecision}
Out[43]= {0, ∞}You can control precision within a complex calculation (without
using N[] on every intermediate
result) by changing these values; however, you should only do so
within a Block (a local context).
For example, compare the difference between a calculation with
automatic precision for intermediate results to the same calculation
with fixed precision (obtained by making $MinPrecision == $MaxPrecision). Note that we must still
start out the calculation with base values of at least $MinPrecision,
otherwise the value will revert to the lowest precision, as explained
in 1.2 Mixing Different Numerical Types.
In[44]:= SetPrecision[(1 + Exp[Sqrt[2] + Sqrt[3]]) / 2^25, 32] Out[44]= 7.226780742612584668840452114476x10–7 In[45]:= Block[{$MinPrecision = 32, $MaxPrecision = 32}, SetPrecision[(1 + Exp[Sqrt[2] + Sqrt[3]])/2^25, 32]] Out[45]= 7.2267807426125846688404521144759x10–7
However, unless you have a very specific reason to control precision yourself, it is generally best to let Mathematica automatically handle this for you.
See Also
The Wolfram documentation for N[] is here: http://bit.ly/XVe2E.
Discussions of precision and accuracy can be found at http://bit.ly/15qq2N and http://bit.ly/icrh1 .
The most thorough discussions of precision and accuracy in Mathematica can be found in Chapter 8 of An Introduction to Programming with Mathematica (Cambridge University Press) and The Mathematica GuideBook for Numerics (Springer).
A nice essay by David Goldberg called “What Every Computer Scientist Should Know About Floating-Point Arithmetic” can be found at https://oreil.ly/5HuG4 .
1.2 Mixing Different Numerical Types
Problem
You need to predict what Mathematica will do with expressions containing mixed types and representations.
Solution
The general rule of thumb is that the least precise type will determine the type of the result.
Mixing exact values and symbols
When expressions containing exact numeric values (integers and rationals) are mixed with symbols, Mathematica will keep all results in the most general form, possibly reducing rationals to integers but leaving symbolic values in symbolic form.
Mixing exact values and approximate values
When an approximate value is used in an otherwise symbolic expression, it forces Mathematica to convert to approximate values.
In[48]:= (2.0 Pi) / 3 + Pi / 3 Out[48]= 3.14159 In[49]:= 1. + (2 Pi) / 3 + Pi / 3 Out[49]= 4.14159
Mixing values of different precision and accuracy
When you mix values of different precision and accuracy, the lower precision and accuracy will determine the result. For multiplication, the precision of the result will be exactly the minimum of the precision of each term, whereas the accuracy will be somewhat less.
In[50]:= x = N[Sqrt[2], 30] * N[Sqrt[3], 10] Out[50]= 2.449489743 In[51]:= Precision[x] Out[51]= 10. In[52]:= Accuracy[x] Out[52]= 9.61092
For addition, the accuracy of the result will be exactly the minimum of the accuracy of each term; the precision will be somewhat more.
In[53]:= x = N[Sqrt[5], {Infinity, 30}] + N[Sqrt[7], {Infinity, 10}] Out[53]= 4.8818192886 In[54]:= Precision[x] Out[54]= 10.6886 In[55]:= Accuracy[x] Out[55]= 10.
Discussion
When mixing exact values with inexact values, it is possible to gain precision.
In[56]:= Precision[N[Sqrt[2], 20]] Out[56]= 20. In[57]:= Precision[2 +N[Sqrt[2], 20]] Out[57]= 20.3828
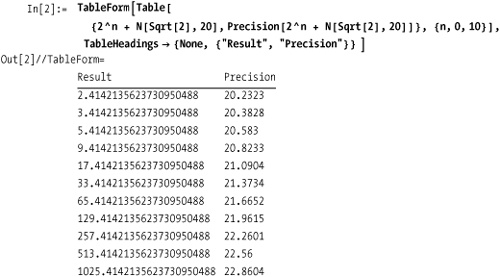
The gain in precision will be greater when the magnitude of the exact number dominates that of the inexact number, as we see in this generated table.
See Also
The most thorough discussions of Mathematica’s numerical rules can be found in Chapter 8 of An Introduction to Programming with Mathematica and The Mathematica GuideBook for Numerics.
1.3 Representing Numbers in Other Bases
Solution
Mathematica uses notation of the form base^^digits to represent
numbers in different bases. There must not be any internal whitespace
in this representation.
In[59]:= 2^^101 (*Binary*) Out[59]= 5 In[60]:= 16^^FFFF (*Hexidecimal*) Out[60]= 65535
Discussion
In addition to expressing numbers in other bases, you can
convert numbers to other bases with BaseForm[ digits, base ]. The base must be an integer between 2 and
36 when using either ^^ or BaseForm[]. Mathematica uses the letters
a through z to represent digits higher than 10.
In[61]:= BaseForm[2^^1010101, 16]
Out[61]//BaseForm=
5516If you do math in another base, the output will still default to
decimal, but you can use BaseForm
to convert the output of a function to hex.
In[62]:= 16^^A0 + 16^^0F // BaseForm[#, 16] & Out[62]//BaseForm= af16 In[63]:= Hash["Hello, my name is Sal", "MD5"] // BaseForm[#, 16] & Out[63]//BaseForm= a275144453239f0279228469f229688116
You can also convert real and complex numbers to other bases.
See Also
1.5 Working with Intervals shows how to extract digits of a number in alternate bases.
1.4 Extracting the Digits of a Number
Problem
You want to extract the individual digits of a number to manipulate them individually.
Solution
The functions IntegerDigits[]
and RealDigits[] make this task
easy.
IntegerDigits[] returns a
list of digits in base 10. See the Discussion section, next, for additional
options.
In[66]:= IntegerDigits[12345]
Out[66]= {1, 2, 3, 4, 5}RealDigits[] returns a
two-item list with the first item being the digits in base 10 and the
second being the position of the decimal point. See the Discussion section for additional options. First
consider the digits display with N[] alone.
In[67]:= N[1/31]
Out[67]= 0.0322581Notice how RealDigits[]
automatically extracts more precision to return the number of digits
necessary to get to the point at which they begin to repeat in the
decimal expansion.
In[68]:= RealDigits[N[1 / 31], 10]
Out[68]= {{3, 2, 2, 5, 8, 0, 6, 4, 5, 1, 6, 1, 2, 9, 0, 3}, -1}Discussion
Both RealDigits[] and
IntegerDigits[] take the desired
base and the number of desired digits (length) as optional second and
third arguments, respectively.
In[69]:= 12 ! Out[69]= 479 001 600 In[70]:= IntegerDigits[12!, 10, 5] Out[70]= {0, 1, 6, 0, 0} In[71]:= 12! // BaseForm[#, 16] & (*Consider 12! in base 16.*) Out[71]//BaseForm= 1c8cfc0016 In[72]:= IntegerDigits[12!, 16] (*Notice how IntegerDigits with base 16 gives the digit values in base 10.*) Out[72]= {1, 12, 8, 12, 15, 12, 0, 0} In[73]:= IntegerDigits[12!, 16] // BaseForm[#, 16]& (*But you can easily force them to base 16.*) Out[73]//BaseForm= {116, c16, 816, c16, f16, c16, 016, 016}
RealDigits can take
an additional fourth argument that specifies where in the decimal
expansion to start. If b
is the base, then the fourth argument n means to start the counting at
the coefficient signified by b^n . The following examples
should clarify.
In[74]:= N[Pi, 10] (*Pi to 10 digits of precision.*) Out[74]= 3.141592654 In[75]:= RealDigits[Pi, 10, 3] (*Extract first three digits. Decimal place is indicated as 1.*) Out[75]= {{3, 1, 4}, 1}
Start at 10^-2 = 0.01, or the
second digit after the decimal.
In[76]:= RealDigits[Pi, 10, 3, -2] (*Extract third to fifth digit. Decimal place is indicated as -2.*) Out[76]= {{4, 1, 5}, -1}
Start at 10^-5 = 0.00001, or
the fifth digit after the decimal.
In[77]:= RealDigits [Pi, 10, 3, -5] Out[77]= {{9, 2, 6}, -4} In[78]:= N[Pi,10] // BaseForm[#, 2] & Out[78]//BaseForm= 11.00100100001111110110101010001002
Here we get the digits of pi in base 2.
In[79]:= RealDigits[Pi, 2, 5, -2]
Out[79]= {{0, 1, 0, 0, 1}, -1}Here is an interesting application in which IntegerDigits is combined with the Tuples
function and a bit of pattern matching to get all n digits without calling
IntegerDigits[] more
than once. We used Short to elide
the full list. (Short places
<<n>>
in the output to indicate n missing items.)
In[80]:= Tuples[IntegerDigits[43210], 4] // Short[#, 4] &
Out[80]//Short=
{{4, 4, 4, 4}, {4, 4, 4, 3}, {4, 4, 4, 2}, {4, 4, 4, 1}, {4, 4, 4, 0}, {4, 4, 3, 4},
{4, 4, 3, 3}, {4, 4, 3, 2}, {4, 4, 3, 1}, {4, 4, 3, 0}, {4, 4, 2, 4},
{4, 4, 2, 3}, {4, 4, 2, 2}, {4, 4, 2, 1}, {4, 4, 2, 0}, {4, 4, 1, 4},
{4, 4, 1, 3}, {4, 4, 1, 2}, {4, 4, 1, 1}, {4, 4, 1, 0}, {4, 4, 0, 4},
{4, 4, 0, 3}, {4, 4, 0, 2}, <<579>>, {0, 0, 4, 2}, {0, 0, 4, 1}, {0, 0, 4, 0},
{0, 0, 3, 4}, {0, 0, 3, 3}, {0, 0, 3, 2}, {0, 0, 3, 1}, {0, 0, 3, 0},
{0, 0, 2, 4}, {0, 0, 2, 3}, {0, 0, 2, 2}, {0, 0, 2, 1}, {0, 0, 2, 0},
{0, 0, 1, 4}, {0, 0, 1, 3}, {0, 0, 1, 2}, {0, 0, 1, 1}, {0, 0, 1, 0},
{0, 0, 0, 4}, {0, 0, 0, 3}, {0, 0, 0, 2}, {0, 0, 0, 1}, {0, 0, 0, 0}}If you do not want the cases with leading zeros, you can use
DeleteCases as follows.
In[81]:= DeleteCases[Tuples[IntegerDigits[43210], 4], {z__ /; z == 0, n__}] // Short[#, 4] & Out[81]//Short= {{4, 4, 4, 4}, {4, 4, 4, 3}, {4, 4, 4, 2}, {4, 4, 4, 1}, {4, 4, 4, 0}, {4, 4, 3, 4}, {4, 4, 3, 3}, {4, 4, 3, 2}, {4, 4, 3, 1}, {4, 4, 3, 0}, {4, 4, 2, 4}, {4, 4, 2, 3}, {4, 4, 2, 2}, {4, 4, 2, 1}, {4, 4, 2, 0}, {4, 4, 1, 4}, {4, 4, 1, 3}, {4, 4, 1, 2}, {4, 4, 1, 1}, {4, 4, 1, 0}, {4, 4, 0, 4}, {4, 4, 0, 3}, {4, 4, 0, 2}, <<454>>, {1, 0, 4, 2}, {1, 0, 4, 1}, {1, 0, 4, 0}, {1, 0, 3, 4}, {1, 0, 3, 3}, {1, 0, 3, 2}, {1, 0, 3, 1}, {1, 0, 3, 0}, {1, 0, 2, 4}, {1, 0, 2, 3}, {1, 0, 2, 2}, {1, 0, 2, 1}, {1, 0, 2, 0}, {1, 0, 1, 4}, {1, 0, 1, 3}, {1, 0, 1, 2}, {1, 0, 1, 1}, {1, 0, 1, 0}, {1, 0, 0, 4}, {1, 0, 0, 3}, {1, 0, 0, 2}, {1, 0, 0, 1}, {1, 0, 0, 0}}
The inverse of IntegerDigits[] is FromDigits[].
In[82]:= FromDigits[IntegerDigits[987654321]] Out[82]= 987 654 321 In[83]:= FromDigits[IntegerDigits[987654321, 2], 2] (*Base 2*) Out[83]= 987 654 321
FromDigits[] has the added
capability of converting strings and roman numerals.
In[84]:= FromDigits["4750"] + 1 Out[84]= 4751 In[85]:= FromDigits["MMXIX", "Roman"] – 10 Out[85]= 2009
IntegerString[] is
used to convert back to string form. I use InputForm only so the quotes are
displayed.
In[86]:= IntegerString[4750] //InputForm Out[86]//InputForm= "4750" In[87]:= IntegerString[2009, "Roman"] // InputForm Out[87]//InputForm= "MMIX"
1.5 Working with Intervals
Problem
You need to compute with data subject to measurement errors and you need the greatest possible estimate on the final error.
Solution
As an alternative to doing math directly on numbers, Mathematica allows you to do math on intervals that define the uncertainty in a value.
In[88]:= Clear[error1, error2, mass, velocity, kineticEnergy]; error1 = 0.01; error2 = 0.005; mass = Interval[{1.10 - error1, 1.10 + error1}]; velocity = Interval[{7.50 - error2, 7.50 + error2}]; kineticEnergy = 1/2 mass velocity ^ 2 Out[92]= Interval[{30.6154, 31.2604}]
By representing them as intervals, we express the idea that there are some known errors in the measurement of the value of mass and velocity. We would like to understand what that means in terms of the value we compute for kinetic energy.
You can see that the resulting error range is magnified by the combination of each error and the squaring.
In[93]:= Subtract @@ kineticEnergy[[1]] // Abs (*This computes the size of the interval.*) Out[93]= 0.645
If there were only a single interval of uncertainty, the range would be smaller.
In[94]:= Clear[error1, mass, velocity, kineticEnergy]; error1 = 0.01; mass = Interval[{1.10 - error1, 1.10 + error1}]; velocity = 7.5; kineticEnergy = 1/2 mass velocity^2 Out[98]= Interval[{30.6562, 31.2188}] In[99]:= Subtract @@ kineticEnergy[[1]] // Abs Out[99]= 0.5625
Discussion
Intervals are objects with head Interval and a sequence of one or more lists
that represent segments of the interval. Typically there is one list,
but non-overlapping intervals can be expressed using two or more
lists.
In[100]:= Interval[{1, 2}] Out[100]= Interval[{1, 2}] In[101]:= Interval[{1, 2}, {3, 4}] Out[101]= Interval[{1, 2}, {3, 4}]
Intervals will automatically reorder themselves so that the least value is first.
In[102]:= Interval[{2, 1}] Out[102]= Interval[{1, 2}] In[103]:= Interval[{4, 3}, {2, 1}] Out[103]= Interval[{1, 2}, {3, 4}]
Naturally, the standard mathematical operations for scalars work on intervals as well.
There are also functions specifically for working with
intervals. IntervalUnion[] gives
the interval representing set of all points of the input intervals.
IntervalIntersection[] gives the
interval in common among the inputs and IntervalMemberQ[] tests if a value belongs
to an interval.
There are some cases in which Mathematica functions can return intervals. Consider the problem of finding the limit of an oscillating function at a critical value.
See Also
Papers and FAQs (as well as a movie) related to the theory of interval math can be found at https://oreil.ly/LmZ4N.
1.6 Converting Between Numerical Types
Problem
You have a number of one type and need it represented in another type.
Solution
Conversion from rational to integer happens automatically, when possible.
In[111]:= Head[4/2]
Out[111]= IntegerConversion of rational to integer can be forced by using
Floor[], Ceiling[], and Round[]. (Numbers of the form
x .5 are rounded toward the nearest even
integer.)
In[112]:= Floor[5/2] Out[112]= 2 In[113]:= Ceiling[5/2] Out[113]= 3 In[114]:= Round[5/2] Out[114]= 2 In[115]:= Round[7/2] Out[115]= 4
We already saw in 1.1 Controlling Precision and Accuracy how N[] can be used to convert exact values and
symbolic constants to approximate real numbers. Rationalize[] is how you convert from
approximate values to exact.
The single argument version of Rationalize will only succeed if a
sufficiently close (see Discussion section,
next) rational number exists.
In[117]:= Rationalize[3.1415927]
Out[117]= 3.14159You can provide a second argument specifying your tolerance for error, in which case the operation will always succeed.
And you can force an exact rational by indicating a maximum error of zero.
Discussion
On the surface, the solutions here are rather simple. In
day-to-day usage, numeric conversion will not present many challenges.
However, there are subtle issues and interesting theory underlying the
apparent simplicity. Let’s consider rounding. Suppose you need to
round a set of numbers, but the numbers still must satisfy some
constraint after the rounding. Consider percentages or probabilities.
One would want percentages to still add to 100 and probabilities to
still sum to 1. Another context is in statistics, where we want to
round while preserving certain statistical properties, such as the
variance. Various forms of stochastic rounding can be used in these
cases. One form of stochastic rounding that gives good results is the
unbiased rounding rule. According to this rule, a
number of the form x.v
is rounded up with the probability v /10 and rounded down with probability
(10-v)/10. So, for example, 10.5
would have equal probability of going to 10 as to 11, whereas 10.85
would have probability of 0.85 of rounding up and 0.15 of rounding
down.
In[120]:= UnbiasedRound[x_] := Block[{whole = Floor[x], v}, v = 10 * (x - whole); whole + Floor[v/10 + RandomReal[]]] In[121]:= Table[UnbiasedRound[10.5], {20}] Out[121]= {11, 11, 10, 11, 10, 10, 10, 11, 11, 11, 10, 11, 11, 10, 10, 11, 11, 11, 11, 11} In[122]:= Table[UnbiasedRound[10.1], {20}] Out[122]= {10, 10, 10, 10, 10, 10, 10, 10, 10, 10, 10, 11, 10, 10, 10, 10, 11, 10, 10, 10} In[123]:= Table[UnbiasedRound[10.8], {20}] Out[123]= {11, 11, 11, 10, 11, 11, 11, 11, 11, 10, 11, 10, 11, 11, 10, 11, 11, 11, 11, 11}
The main disadvantage of stochastic rounding is that the results are not repeatable.
See Also
An Examination of the Effects of Rounding on the Quality and Confidentiality of Tabular Data by Lawrence H. Cox and Jay J. Kim ( https://oreil.ly/6Saie ).
1.7 Displaying Numbers in Alternate Forms
Problem
You don’t like the format that Mathematica chooses to display a particular numerical result.
Solution
Use one of the alternative forms: AccountingForm, EngineeringForm, NumberForm, PaddedForm, and ScientificForm. The default form is usually
the most compact way to represent the number, but if you are
outputting values that have specific user expectations or if you are
trying to convey a specific accuracy, you may want to force a
different form.
In[124]:= number = 3.50 * 1000000
Out[124]= 3.5x106Accounting form does not use scientific notation and shows
negative numbers in parentheses. Here it is traditional to use the
form as a postfix (//)
operation.
In[125]:= number // AccountingForm Out[125]//AccountingForm= 3500000. In[126]:= -number // AccountingForm Out[126]//AccountingForm= (3500000.)
Alternatively, NumberForm allows you to control the digits
of precision and the number of digits after the decimal.
In[127]:= NumberForm[number, {6, 4}]
Out[127]//NumberForm=
3.5000x106Discussion
Forms have an extensive set of options to provide fine-grained
control over the output. Here I use AccountingForm to display a column of
numbers. DigitBlock specifies the
grouping factor and NumberPadding
allows control of the characters used to pad out the display on the
left (shown here as spaces) and right (shown as zeros).
Contrast this to AccountingForm without the options.
In[129]:= AccountingForm [Column [{100000.00, 1000000.00, 10000000.00}]]
Out[129]//AccountingForm=
100000.
1000000.
10000000.PaddedForm is convenient when
all you want to do is pad out a number with specific characters on the
left and right. This is often a useful operation prior to conversion
to a string to generate fixed-length identifiers.
EngineeringForm
forces exponents in multiples of three, provided an exponent of at
least three is required.
In[132]:= {10.0, 100.0, 1000.0, 10 000.0, 100 000.0, 1 000 000.0} // EngineeringForm
Out[132]//EngineeringForm=
{10., 100., 1.×103, 10.×103, 100.×103, 1.×106}ScientificForm always shows
numbers with one digit before the decimal and adjusts the exponent
accordingly.
In[133]:= {10.0, 100.0, 1000.0, 10 000.0, 100 000.0, 1 000 000.0} // ScientificForm
Out[133]//ScientificForm=
{1.×101, 1.×102, 1.×103, 1.×104, 1.×105, 1.×106}You can use the option NumberFormat to get precise control of the
display. NumberFormat specifies a
function (see Chapter 2 for details)
that accepts up to three arguments for the mantissa, base, and
exponent. Here is an example that displays numbers like a calculator
might. Here, the function uses Row
to format the mantissa and exponent (it ignores the base).
See Also
You can find information and examples on all these forms and their options in the Wolfram documentation under tutorial/OutputFormatsForNumbers.
Get Mathematica Cookbook now with the O’Reilly learning platform.
O’Reilly members experience books, live events, courses curated by job role, and more from O’Reilly and nearly 200 top publishers.