Mathematical Methods in Science and Engineering, 2nd Edition

Chapter 14Infinite Series

In physics and engineering, sometimes physical properties can only be expressed in terms of infinite sums. We also frequently encounter differential or integral equations that can only be solved by the method of infinite series. In working with infinite series, the first thing that needs to be checked is their convergence. In this regard, we start by introducing the commonly used tests of convergence for series of numbers and then extend our discussion to series of functions and power series. We then introduce some analytic techniques for evaluating infinite sums. We also discuss asymptotic series and the method of steepest descent and saddle-point integrals. We also introduce the Padé approximants, which is a very effective tool in finding sums of series whose only a few terms are known. Infinite products, which are closely related to infinite series, are also discussed in this chapter. In conjunction with the Casimir effect, we show how finite and meaningful results can be obtained from some of the divergent series in physics by the method of regularization and renormalization.

14.1 Convergence of Infinite Series

We write an infinite series with the general term as

14.1

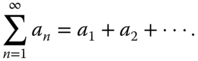
Summation of the first terms is called the th partial sum of the series. If the ...