Chapter 7. Mining GitHub: Inspecting Software Collaboration Habits, Building Interest Graphs, and More
GitHub has rapidly evolved in recent years to become the de facto social coding platform with a deceptively simple premise: provide a top-notch hosted solution for developers to create and maintain open source software projects with an open source distributed version control system called Git. Unlike version control systems such as CVS or Subversion, with Git there is no canonical copy of the code base, per se. All copies are working copies, and developers can commit local changes on a working copy without needing to be connected to a centralized server.
The distributed version control paradigm lends itself exceptionally well to GitHub’s notion of social coding because it allows developers who are interested in contributing to a project to fork a working copy of its code repository and immediately begin working on it in just the same way that the developer who owns the fork works on it. Git not only keeps track of semantics that allow repositories to be forked arbitrarily but also makes it relatively easy to merge changes from a forked child repository back into its parent repository. Through the GitHub user interface, this workflow is called a pull request.
It is a deceptively simple notion, but the ability for developers to create and collaborate on coding projects with elegant workflows that involve minimal overhead (once you understand some fundamental details about how Git works) has certainly streamlined many of the tedious details that have hindered innovation in open source development, including conveniences that transcend into the visualization of data and interoperability with other systems. In other words, think of GitHub as an enabler of open source software development. In the same way, although developers have collaborated on coding projects for decades, a hosted platform like GitHub supercharges collaboration and enables innovation in unprecedented ways by making it easy to create a project, share out its source code, maintain feedback and an issue tracker, accept patches for improvements and bug fixes, and more. More recently, it even appears that GitHub is increasingly catering to non-developers—and becoming one of the hottest social platforms for mainstream collaboration.
Just to be perfectly clear, this chapter does not attempt to provide a tutorial on how to use Git or GitHub as a distributed version control system or even discuss Git software architecture at any level. (See one of the many excellent online Git references, such as gitscm.com, for that kind of instruction.) This chapter does, however, attempt to teach you how to mine GitHub’s API to discover patterns of social collaboration in the somewhat niche software development space.
Note
Always get the latest bug-fixed source code for this chapter (and every other chapter) online at http://bit.ly/MiningTheSocialWeb2E. Be sure to also take advantage of this book’s virtual machine experience, as described in Appendix A, to maximize your enjoyment of the sample code.
Overview
This chapter provides an introduction to GitHub as a social coding platform and to graph-oriented analysis using NetworkX. In this chapter, you’ll learn how to take advantage of GitHub’s rich data by constructing a graphical model of the data that can be used in a variety of ways. In particular, we’ll treat the relationships between GitHub users, repositories, and programming languages as an interest graph, which is a way of interpreting the nodes and links in the graph primarily from the vantage point of people and the things in which they are interested. There is a lot of discussion these days amongst hackers, entrepreneurs, and web mavens as to whether or not the future of the Web is largely predicated upon some notion of an interest graph, so now is a fine time to get up to speed on the emerging graph landscape and all that it entails.
In sum, then, this chapter follows the same predictable template as chapters before it and covers:
GitHub’s developer platform and how to make API requests
Graph schemas and how to model property graphs with NetworkX
The concept of an interest graph and how to construct an interest graph from GitHub data
Using NetworkX to query property graphs
Graph centrality algorithms, including degree, betweenness, and closeness centrality
Exploring GitHub’s API
Like the other social web properties featured in this book, GitHub’s developer site offers comprehensive documentation on its APIs, the terms of service governing the use of those APIs, example code, and much more. Although the APIs are fairly rich, we’ll be focusing on only the few API calls that we need in order to collect the data for creating some interest graphs that associate software developers, projects, programming languages, and other aspects of software development. The APIs more or less provide you with everything you’d need to build a rich user experience just like github.com offers itself, and there is no shortage of compelling and possibly even lucrative applications that you could build with these APIs.
The most fundamental primitives for GitHub are users and projects. If you are reading this page, you’ve probably already managed to pull down this book’s source code from its GitHub project page, so this discussion assumes that you’ve at least visited a few GitHub project pages, have poked around a bit, and are familiar with the general notion of what GitHub offers.
A GitHub user has a public profile that generally includes one or more code repositories that have either been created or forked from another GitHub user. For example, the GitHub user ptwobrussell owns a couple of GitHub repositories, including one called Mining-the-Social-Web and another called Mining-the-Social-Web-2nd-Edition. ptwobrussell has also forked a number of repositories in order to capture a particular working snapshot of certain code bases for development purposes, and these forked projects also appear in his public profile.
Part of what makes GitHub so powerful is that ptwobrussell is free to do anything he’d like with any of these forked projects (subject to the terms of their software licenses), in the same way that anyone else could do the same thing to forked projects. When a user forks a code repository, that user effectively owns a working copy of the same repository and can do anything from just fiddle around with it to drastically overhaul and create a long-lived fork of the original project that may never be intended to get merged back into the original parent repository. Although most project forks never materialize into derivative works of their own, the effort involved in creating a derivative work is trivial from the standpoint of source code management. It may be short-lived and manifest as a pull request that is merged back into the parent, or it may be long-lived and become an entirely separate project with its own community. The barrier to entry for open source software contribution and other projects that increasingly find themselves appearing on GitHub is low indeed.
In addition to forking projects on GitHub, a user can also bookmark or star a project to become what is known as a stargazer of the project. Bookmarking a project is essentially the same thing as bookmarking a web page or a tweet. You are signifying interest in the project, and it’ll appear on your list of GitHub bookmarks for quick reference. What you’ll generally notice is that far fewer people fork code than bookmark it. Bookmarking is an easy and well-understood notion from over a decade of web surfing, whereas forking the code implies having the intent to modify or contribute to it in some way. Throughout the remainder of this chapter, we’ll focus primarily on using the list of stargazers for a project as the basis of constructing an interest graph for it.
Creating a GitHub API Connection
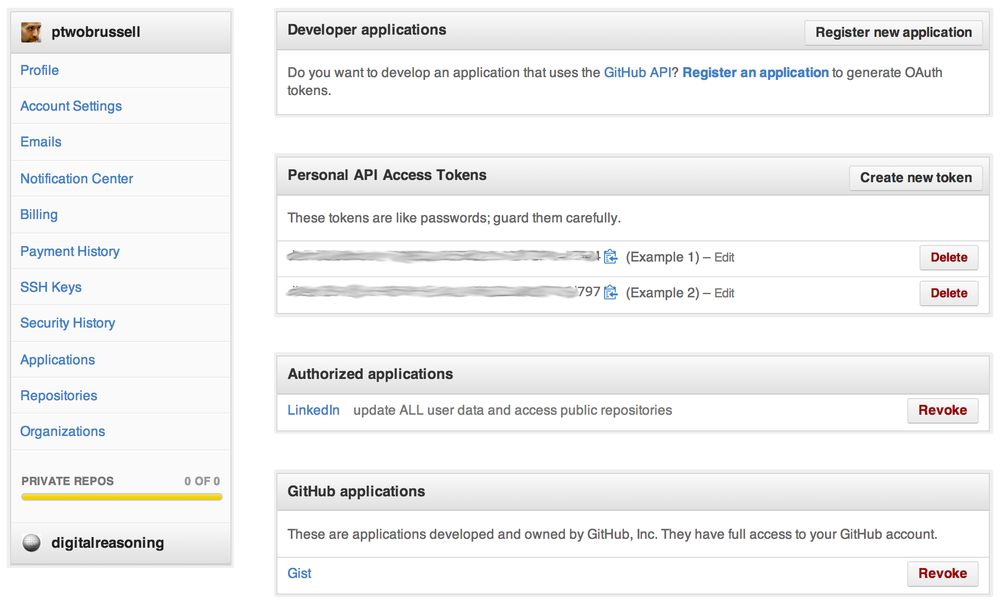
Like other social web properties, GitHub implements OAuth, and the steps to gaining API access involve creating an account followed by one of two possibilities: creating an application to use as the consumer of the API or creating a “personal” access token that will be linked directly to your account. In this chapter, we’ll opt to use a personal access token, which is as easy as clicking a button in the Personal Access API Tokens section of your account’s Applications menu, as shown in Figure 7-1. (See Appendix B for a more extensive overview of OAuth.)
A programmatic option for obtaining an access token as opposed
to creating one within the GitHub user interface is shown in Example 7-1
as an adaptation of “Creating an
OAuth token for command-line use” from GitHub’s help site. (If
you are not taking advantage of the virtual machine experience for this
book, as described in Appendix A, you’ll need to type pip install
requests in a terminal prior to running this
example.)
importrequestsfromgetpassimportgetpassimportjsonusername=''# Your GitHub usernamepassword=''# Your GitHub password# Note that credentials will be transmitted over a secure SSL connectionurl='https://api.github.com/authorizations'note='Mining the Social Web, 2nd Ed.'post_data={'scopes':['repo'],'note':note}response=requests.post(url,auth=(username,password),data=json.dumps(post_data),)"API response:",response.text"Your OAuth token is",response.json()['token']# Go to https://github.com/settings/applications to revoke this token
As is the case with many other social web properties, GitHub’s
API is built on top of HTTP and accessible through any programming
language in which you can make an HTTP request, including command-line
tools in a terminal. Following the precedents set by previous chapters,
however, we’ll opt to take advantage of a Python library so that we can
avoid some of the tedious details involved in making requests, parsing
responses, and handling pagination. In this particular case, we’ll use PyGithub, which can be installed with
the somewhat predictable pip install
PyGithub. We’ll start by taking at a couple of examples of how to make
GitHub API requests before transitioning into a discussion of graphical
models.
Let’s seed an interest graph in this chapter from the Mining-the-Social-Web GitHub repository and create connections between it and its stargazers. Listing the stargazers for a repository is possible with the List Stargazers API. You could try out an API request to get an idea of what the response type looks like by copying and pasting the following URL in your web browser: https://api.github.com/repos/ptwobrussell/Mining-the-Social-Web/stargazers.
Note
Although you are reading Mining the Social Web, 2nd Edition, at the time of this writing the source code repository for the first edition still has much more activity than the second edition, so the first edition repository will serve as the basis of examples for this chapter. Analysis of any repository, including the repository for the second edition of this book, is easy enough to accomplish by simply changing the name of the initial project as introduced in Example 7-3.
The ability to issue an unauthenticated request in this manner
is quite convenient as you are exploring the API, and the rate limit of 60 unauthenticated requests per hour
is more than adequate for tinkering and exploring. You could, however,
append a query string of the form ?access_token=xxx,
where xxx specifies your access token, to
make the same request in an authenticated fashion. GitHub’s
authenticated rate limits are a generous 5,000 requests per hour, as
described in the developer
documentation for rate limiting. Example 7-2 illustrates a
sample request and response. (Keep in mind that this is requesting only the
first page of results and, as described in the developer documentation for
pagination, metadata information for navigating the pages of
results is included in the HTTP headers.)
importjsonimportrequests# An unauthenticated request that doesn't contain an ?access_token=xxx query stringurl="https://api.github.com/repos/ptwobrussell/Mining-the-Social-Web/stargazers"response=requests.get(url)# Display one stargazerjson.dumps(response.json()[0],indent=1)# Display headersfor(k,v)inresponse.headers.items():k,"=>",v
Sample output follows:
{
"following_url": "https://api.github.com/users/rdempsey/following{/other_user}",
"events_url": "https://api.github.com/users/rdempsey/events{/privacy}",
"organizations_url": "https://api.github.com/users/rdempsey/orgs",
"url": "https://api.github.com/users/rdempsey",
"gists_url": "https://api.github.com/users/rdempsey/gists{/gist_id}",
"html_url": "https://github.com/rdempsey",
"subscriptions_url": "https://api.github.com/users/rdempsey/subscriptions",
"avatar_url": "https://1.gravatar.com/avatar/8234a5ea3e56fca09c5549ee...png",
"repos_url": "https://api.github.com/users/rdempsey/repos",
"received_events_url": "https://api.github.com/users/rdempsey/received_events",
"gravatar_id": "8234a5ea3e56fca09c5549ee5e23e3e1",
"starred_url": "https://api.github.com/users/rdempsey/starred{/owner}{/repo}",
"login": "rdempsey",
"type": "User",
"id": 224,
"followers_url": "https://api.github.com/users/rdempsey/followers"
}
status => 200 OK
access-control-allow-credentials => true
x-ratelimit-remaining => 58
x-github-media-type => github.beta
x-content-type-options => nosniff
access-control-expose-headers => ETag, Link, X-RateLimit-Limit,
X-RateLimit-Remaining, X-RateLimit-Reset,
X-OAuth-Scopes, X-Accepted-OAuth-Scopes
transfer-encoding => chunked
x-github-request-id => 73f42421-ea0d-448c-9c90-c2d79c5b1fed
content-encoding => gzip
vary => Accept, Accept-Encoding
server => GitHub.com
last-modified => Sun, 08 Sep 2013 17:01:27 GMT
x-ratelimit-limit => 60
link => <https://api.github.com/repositories/1040700/stargazers?page=2>;
rel="next",
<https://api.github.com/repositories/1040700/stargazers?page=30>;
rel="last"
etag => "ca10cd4edc1a44e91f7b28d3fdb05b10"
cache-control => public, max-age=60, s-maxage=60
date => Sun, 08 Sep 2013 19:05:32 GMT
access-control-allow-origin => *
content-type => application/json; charset=utf-8
x-ratelimit-reset => 1378670725As you can see, there’s a lot of useful information that GitHub
is returning to us that is not in the body of the HTTP response and is
instead conveyed as HTTP headers, as outlined in the developer
documentation. You should skim and understand what all of the various
headers mean, but a few of note include the status header, which tells us that the request
was OK with a 200 response; headers that involve the rate limit, such as
x-ratelimit-remaining; and the
link header, which contains a value
such as the following:
https://api.github.com/repositories/1040700/stargazers?page=2; rel="next", https://api.github.com/repositories/1040700/stargazers?page=29; rel="last".
The link header’s value is
giving us a preconstructed URL that could be used to fetch the next page
of results as well as an indication of how many total pages of results
there are.
Making GitHub API Requests
Although it’s not difficult to use a library like requests and make the most of this information by parsing it out
ourselves, a library like PyGithub
makes it that much easier for us and tackles the abstraction of the
implementation details of GitHub’s API, leaving us to work with a clean
Pythonic API. Better yet, if GitHub changes the underlying
implementation of its API, we’ll still be able to use PyGithub and our code won’t break.
Before making a request with PyGithub, also take a moment to look at the
body of the response itself. It contains some rich information, but the
piece we’re most interested in is a field called login, which is the GitHub username of the
user who is stargazing at the repository of interest. This information
is the basis of issuing many other queries to other GitHub APIs, such as
“List repositories being
starred,” an API that returns a list of all repositories a user
has starred. This is a powerful pivot because after we have started with
an arbitrary repository and queried it for a list of users who are
interested in it, we are then able to query those users for additional
repositories of interest and potentially discover any patterns that
might emerge.
For example, wouldn’t it be interesting to know what is the next-most-bookmarked repository among all of the users who have bookmarked Mining-the-Social-Web? The answer to that question could be the basis of an intelligent recommendation that GitHub users would appreciate, and it doesn’t take much creativity to imagine different domains in which intelligent recommendations could (and often do) provide enhanced user experiences in applications, as is the case with Amazon and Netflix. At its core, an interest graph inherently lends itself to making such intelligent recommendations, and that’s one of the reasons that interest graphs have become such a conversation topic in certain niche circles of late.
Example 7-3
provides an example of how you could use PyGithub to retrieve all of the stargazers for
a repository to seed an interest graph.
fromgithubimportGithub# XXX: Specify your own access token hereACCESS_TOKEN=''# Specify a username and repository of interest for that user.USER='ptwobrussell'REPO='Mining-the-Social-Web'client=Github(ACCESS_TOKEN,per_page=100)user=client.get_user(USER)repo=user.get_repo(REPO)# Get a list of people who have bookmarked the repo.# Since you'll get a lazy iterator back, you have to traverse# it if you want to get the total number of stargazers.stargazers=[sforsinrepo.get_stargazers()]"Number of stargazers",len(stargazers)
Behind the scenes, PyGithub
takes care of the API implementation details for you and simply exposes
some convenient objects for query. In this case, we create a connection
to GitHub and use the per_page
keyword parameter to tell it that we’d like to receive the maximum
number of results (100) as opposed to the default number (30) in each
page of data that comes back. Then, we get a repository for a particular
user and query for that repository’s stargazers. It is possible for
users to have repositories with identical names, so there is not an
unambiguous way to query by just a repository’s name. Since usernames
and repository names could overlap, you need to take special care to
specify the kind of object that you are working with when using GitHub’s
API if using one of these names as an identifier. We’ll account for this
as we create graphs with node names that may be ambiguous if we do not
qualify them as repositories or users.
Finally, PyGithub generally
provides “lazy iterators” as results, which in this case means that it
does not attempt to fetch all 29 pages of results when the query is
issued. Instead, it waits until a particular page is requested when
iterating over the data before it retrieves that page. For this reason,
we need to exhaust the lazy iterator with a list comprehension in order
to actually count the number of stargazers with the API if we want to
get an exact count.
PyGithub’s documentation is helpful,
its API generally mimics the GitHub API in a predictable way, and you’ll
usually be able to use its pydoc,
such as through the dir()
and help() functions in a Python
interpreter. Alternatively, tab completion and “question mark magic” in
IPython or IPython Notebook will get you to the same place in figuring
out what methods are available to call on what objects. It would be
worthwhile to poke around at the GitHub API a bit with PyGithub to better familiarize yourself with
some of the possibilities before continuing further. As an exercise to
test your skills, can you iterate over Mining-the-Social-Web’s
stargazers (or some subset thereof) and do some basic frequency analysis
that determines which other repositories may be of common interest? You
will likely find Python’s collections.Counter or NLTK’s nltk.FreqDist essential in easily computing frequency statistics.
Modeling Data with Property Graphs
You may recall from Analyzing mutual friendships with directed graphs that graphs were introduced in passing as a means of representing, analyzing, and visualizing social network data from Facebook. This section provides a more thorough discussion and hopefully serves as a useful primer for graph computing. Even though it is still a bit under the radar, the graph computing landscape is emerging rapidly given that graphs are a very natural abstraction for modeling many phenomena in the real world. Graphs offer a flexibility in data representation that is especially hard to beat during data experimentation and analysis when compared to other options, such as relational databases. Graph-centric analyses are certainly not a panacea for every problem, but an understanding of how to model your data with graphical structures is a powerful addition to your toolkit.
Note
A general introduction to graph theory is beyond the scope of this chapter, and the discussion that follows simply attempts to provide a gentle introduction to key concepts as they arise. You may enjoy the short YouTube video “Graph Theory—An Introduction!” if you’d like to accumulate some general background knowledge before proceeding.
The remainder of this section introduces a common kind of graph called a property graph for the purpose of modeling GitHub data as an interest graph by way of a Python package called NetworkX. A property graph is a data structure that represents entities with nodes and relationships between the entities with edges. Each vertex has a unique identifier, a map of properties that are defined as key/value pairs, and a collection of edges. Likewise, edges are unique in that they connect nodes, can be uniquely identified, and can contain properties.
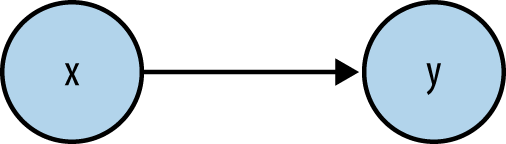
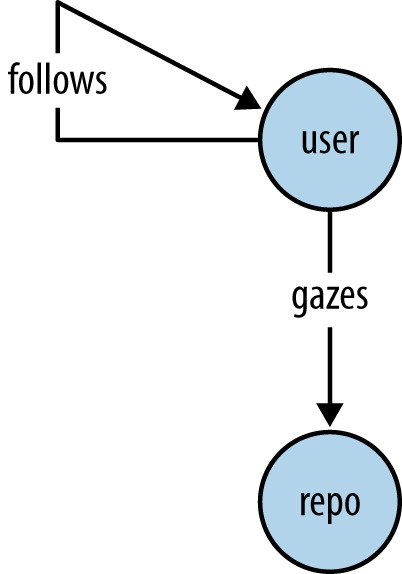
Figure 7-2 shows a trivial example of a property graph with two nodes that are uniquely identified by X and Y with an undescribed relationship between them. This particular graph is called a digraph because its edges are directed, which need not be the case unless the directionality of the edge is rooted in meaning for the domain being modeled.
Expressed in code with NetworkX, a trivial property graph could
be constructed as shown in Example 7-4. (You can use pip install networkx to install this package
if you aren’t using the book’s turnkey virtual machine.)
importnetworkxasnx# Create a directed graphg=nx.DiGraph()# Add an edge to the directed graph from X to Yg.add_edge('X','Y')# Print some statistics about the graphnx.info(g)# Get the nodes and edges from the graph"Nodes:",g.nodes()"Edges:",g.edges()# Get node properties"X props:",g.node['X']"Y props:",g.node['Y']# Get edge properties"X=>Y props:",g['X']['Y']# Update a node propertyg.node['X'].update({'prop1':'value1'})"X props:",g.node['X']# Update an edge propertyg['X']['Y'].update({'label':'label1'})"X=>Y props:",g['X']['Y']
Sample output from the example follows:
Name:Type:DiGraphNumberofnodes:2Numberofedges:1Averageindegree:0.5000Averageoutdegree:0.5000Nodes:['Y','X']Edges:[('X','Y')]Xprops:{}Yprops:{}X=>Yprops:{}Xprops:{'prop1':'value1'}X=>Yprops:{'label':'label1'}
In this particular example, the add_edge
method of the digraph adds an edge from a node that’s uniquely identified
by X to a node that’s uniquely
identified by Y, resulting in a graph
with two nodes and one edge between them. In terms of its unique
identifier, this node would be represented by the tuple (X,
Y) since both nodes that it connects are uniquely
identified themselves. Be aware that adding an edge from Y back to X
would create a second edge in the graph, and this second edge could
contain its own set of edge properties. In general, you wouldn’t want to
create this second edge since you can get a node’s incoming or outgoing
edges and effectively traverse the edge in either direction, but there may
be some situations in which it is more convenient to explicitly include
the additional edge.
The degree of a node in a graph is the number of incident edges to it, and for a directed graph, there is a notion of in degree and out degree since edges have direction. The average in degree and average out degree values provide a normalized score for the graph that represents the number of nodes that have incoming and outgoing edges. In this particular case, the directed graph has a single directed edge, so there is one node with an outgoing edge and one node with an incoming edge.
The in and out degree of a node is a fundamental concept in graph theory. Assuming you know the number of vertices in the graph, the average degree provides a measure of the graph’s density: the number of actual edges compared to the number of possible edges if the graph were fully connected. In a fully connected graph, each node is connected to every other node, and in the case of a directed graph, this means that all nodes have incoming edges from all other nodes.
You calculate the average in degree for an entire graph by summing the values of each node’s in degree and dividing the total by the number of nodes in the graph, which is 1 divided by 2 in Example 7-4. The average out degree calculation is computed the same way except that the sum of each node’s out degree is used as the value to divide by the number of nodes in the graph. When you’re considering an entire directed graph, there will always be an equal number of incoming edges and outgoing edges because each edge connects only two nodes,[27] and the average in degree and average out degree values for the entire graph will be the same.
Note
In the general case, the maximum values for average in and out degree in a graph are one less than the number of nodes in the graph. Take a moment to convince yourself that this is the case by considering the number of edges that are necessary to fully connect all of the nodes in a graph.
In the next section, we’ll construct an interest graph using these same property graph primitives and illustrate these additional methods at work on real-world data. First, take a moment to explore by adding some nodes, edges, and properties to the graph. The NetworkX documentation provides a number of useful introductory examples that you can also explore if this is one of your first encounters with graphs and you’d like some extra instruction as a primer.
Analyzing GitHub Interest Graphs
Now equipped with the tools to both query GitHub’s API and model the data that comes back as a graph, let’s put our skills to the test and begin constructing and analyzing an interest graph. We’ll start with a repository that will represent a common interest among a group of GitHub users and use GitHub’s API to discover the stargazers for this repository. From there, we’ll be able to use other APIs to model social connections between GitHub users who follow one another and hone in on other interests that these users might share.
We’ll also learn about some fundamental techniques for analyzing graphs called centrality measures. Although a visual layout of a graph is tremendously useful, many graphs are simply too large or complex for an effective visual inspection, and centrality measures can be helpful in analytically measuring aspects of the network structure. (But don’t worry, we will also visualize a graph before closing this chapter.)
Seeding an Interest Graph
Recall that an interest graph and a social graph are not the same thing. Whereas a social graph’s primary focus is representing connections between people and it generally requires a mutual relationship between the parties involved, an interest graph connects people and interests and involves unidirectional edges. Although the two are by no means totally disjoint concepts, do not confuse the connection between a GitHub user following another GitHub user with a social connection—it is an “interested in” connection because there is not a mutual acceptance criterion involved.
Note
A classic example of a hybridized graphical model that would qualify as a social interest graph is Facebook. It started primarily as a technology platform based upon the concept of a social graph, but the incorporation of the Like button squarely catapulted it into hybrid territory that could be articulated as a social-interest graph. It explicitly represents connections between people as well as connections between people and the things that they are interested in. Twitter has always been some flavor of an interest graph with its asymmetric “following” model, which can be interpreted as a connection between a person and the things (which could be other people) that person is interested in.
Examples 7-5 and 7-6 will introduce code samples to construct the initial “gazes” relationships between users and repositories, demonstrating how to explore the graphical structure that emerges. The graph that is initially constructed can be referred to as an ego graph in that there is a central point of focus (an ego) that is the basis for most (in this case, all) of the edges. An ego graph is sometimes called a “hub and spoke graph” or a “star graph” since it resembles a hub with spokes emanating from it and looks like a star when rendered visually.
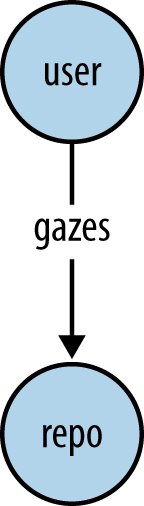
From the standpoint of a graph schema, the graph contains two types of nodes and one type of edge, as is demonstrated in Figure 7-3.
Note
We’ll use the graph schema shown in Figure 7-3 as a starting point and evolve it with modifications throughout the remainder of this chapter.
There is a subtle but important constraint in data modeling that
involves the avoidance of naming collisions: usernames and repository
names may (and often do) collide with one another. For example, there
could be a GitHub user named “ptwobrussell,” as well as multiple
repositories named “ptwobrussell”. Recalling that the add_edge method uses the items passed in as
its first two parameters as unique identifiers, we can append either
“(user)” or “(repo)” to the items to ensure that all nodes in the graph
will be unique. From the standpoint of modeling with NetworkX, appending
a type for the node mostly takes care of the problem.
Along the same lines, repositories that are owned by different users can have the same name whether they are forks of the same code base or entirely different code bases. At the moment this particular detail is of no concern to us, but once we begin to add in other repositories that other GitHub users are stargazing at, the possibility of this kind of collision will increase.
Whether to allow these types of collisions or to implement a graph construction strategy that avoids them is a design decision that carries with it certain consequences. For example, it would probably be desirable to have forks of the same repository collapse into the same node in the graph as opposed to representing them all as different repositories, but you would certainly not want completely different projects that shared a name to collapse into the same node.
Note
Given the limited scope of the problem that we are solving and that it’s initially focusing on a particular repository of interest, we’ll opt to avoid the complexity that disambiguating repository names introduces.
With that in mind, take a look at Example 7-5, which constructs an ego graph of a repository and its stargazers, and Example 7-6, which introduces some useful graph operations.
# Expand the initial graph with (interest) edges pointing each direction for# additional people interested. Take care to ensure that user and repo nodes# do not collide by appending their type.importnetworkxasnxg=nx.DiGraph()g.add_node(repo.name+'(repo)',type='repo',lang=repo.language,owner=user.login)forsginstargazers:g.add_node(sg.login+'(user)',type='user')g.add_edge(sg.login+'(user)',repo.name+'(repo)',type='gazes')
# Poke around in the current graph to get a better feel for how NetworkX worksnx.info(g)g.node['Mining-the-Social-Web(repo)']g.node['ptwobrussell(user)']g['ptwobrussell(user)']['Mining-the-Social-Web(repo)']# The next line would throw a KeyError since no such edge exists:# print g['Mining-the-Social-Web(repo)']['ptwobrussell(user)']g['ptwobrussell(user)']g['Mining-the-Social-Web(repo)']g.in_edges(['ptwobrussell(user)'])g.out_edges(['ptwobrussell(user)'])g.in_edges(['Mining-the-Social-Web(repo)'])g.out_edges(['Mining-the-Social-Web(repo)'])
The following sample (abbreviated) output demonstrates some of the possibilities based upon the graph operations just shown:
Name:Type:DiGraphNumberofnodes:852Numberofedges:851Averageindegree:0.9988Averageoutdegree:0.9988{'lang':u'JavaScript','owner':u'ptwobrussell','type':'repo'}{'type':'user'}{'type':'gazes'}{u'Mining-the-Social-Web(repo)':{'type':'gazes'}}{}[][('ptwobrussell(user)',u'Mining-the-Social-Web(repo)')][(u'gregmoreno(user)','Mining-the-Social-Web(repo)'),(u'SathishRaju(user)','Mining-the-Social-Web(repo)'),...][]
With an initial interest graph in place, we can get creative in determining which steps might be most interesting to take next. What we know so far is that there are approximately 850 users who share a common interest in social web mining, as indicated by their stargazing association to ptwobrussell’s Mining-the-Social-Web repository. As expected, the number of edges in the graph is one less than the number of nodes. The reason that this is the case is because there is a one-to-one correspondence at this point between the stargazers and the repository (an edge must exist to connect each stargazer to the repository).
If you recall that the average in degree and average out degree metrics yield a normalized value that provides a measure for the density of the graph, the value of 0.9988 should confirm our intuition. We know that we have 851 nodes corresponding to stargazers that each have an out degree equal to 1, and one node corresponding to a repository that has an in degree of 851. In other words, we know that the number of edges in the graph is one less than the number of nodes. The density of edges in the graph is quite low given that the maximum value for the average degree in this case is 851.
It might be tempting to think about the topology of the graph, knowing that it looks like a star if visually rendered, and try to make some kind of connection to the value of 0.9988. It is true that we have one node that is connected to all other nodes in the graph, but it would be a mistake to generalize and try to make some kind of connection to the average degree being approximately 1.0 based on this single node. It could just as easily have been the case that the 851 nodes could have been connected in many other configurations to arrive at a value of 0.9988. To gain insight that would support this kind of conclusion we would need to consider additional analytics, such as the centrality measures introduced in the next section.
Computing Graph Centrality Measures
A centrality measure is a fundamental graph analytic that provides insight into the relative importance of a particular node in a graph. Let’s consider the following centrality measures, which will help us more carefully examine graphs to gain insights about networks:
- Degree centrality
The degree centrality of a node in the graph is a measure of the number of incident edges upon it. Think of this centrality measure as a way of tabulating the frequency of incident edges on nodes for the purpose of measuring uniformity among them, finding the nodes with the highest or lowest numbers of incident edges, or otherwise trying to discover patterns that provide insight into the network topology based on number of connections as a primary motivation. The degree centrality of a node is just one facet that is useful in reasoning about its role in a network, and it provides a good starting point for identifying outliers or anomalies with respect to connectedness relative to other nodes in the graph. In aggregate, we also know from our earlier discussion that the average degree centrality tells us something about the density of an overall graph. NetworkX provides
networkx.degree_centralityas a built-in function to compute the degree centrality of a graph. It returns a dictionary that maps the ID of each node to its degree centrality.- Betweenness centrality
The betweenness centrality of a node is a measure of how often it connects any other nodes in the graph in the sense of being in between other nodes. You might think about betweenness centrality as a measure of how critical a node is in connecting other nodes as a broker or gateway. Although not necessarily the case, the loss of nodes with a high betweenness centrality measure could be quite disruptive to the flow of energy[28] in a graph, and in some circumstances removing nodes with high betweenness centrality can disintegrate a graph into smaller subgraphs. NetworkX provides
networkx.betweenness_centralityas a built-in function to compute the betweenness centrality of a graph. It returns a dictionary that maps the ID of each node to its betweenness centrality.- Closeness centrality
The closeness centrality of a node is a measure of how highly connected (“close”) it is to all other nodes in the graph. This centrality measure is also predicated on the notion of shortest paths in the graph and offers insight into how well connected a particular node is in the graph. Unlike a node’s betweenness centrality, which tells you something about how integral it is in connecting nodes as a broker or gateway, a node’s closeness centrality accounts more for direct connections. Think of closeness in terms of a node’s ability to spread energy to all other nodes in a graph. NetworkX provides
networkx.closeness_centralityas a built-in function to compute the closeness centrality of a graph. It returns a dictionary that maps the ID of each node to its closeness centrality.
Note
NetworkX provides a number of powerful centrality measures in its online documentation.
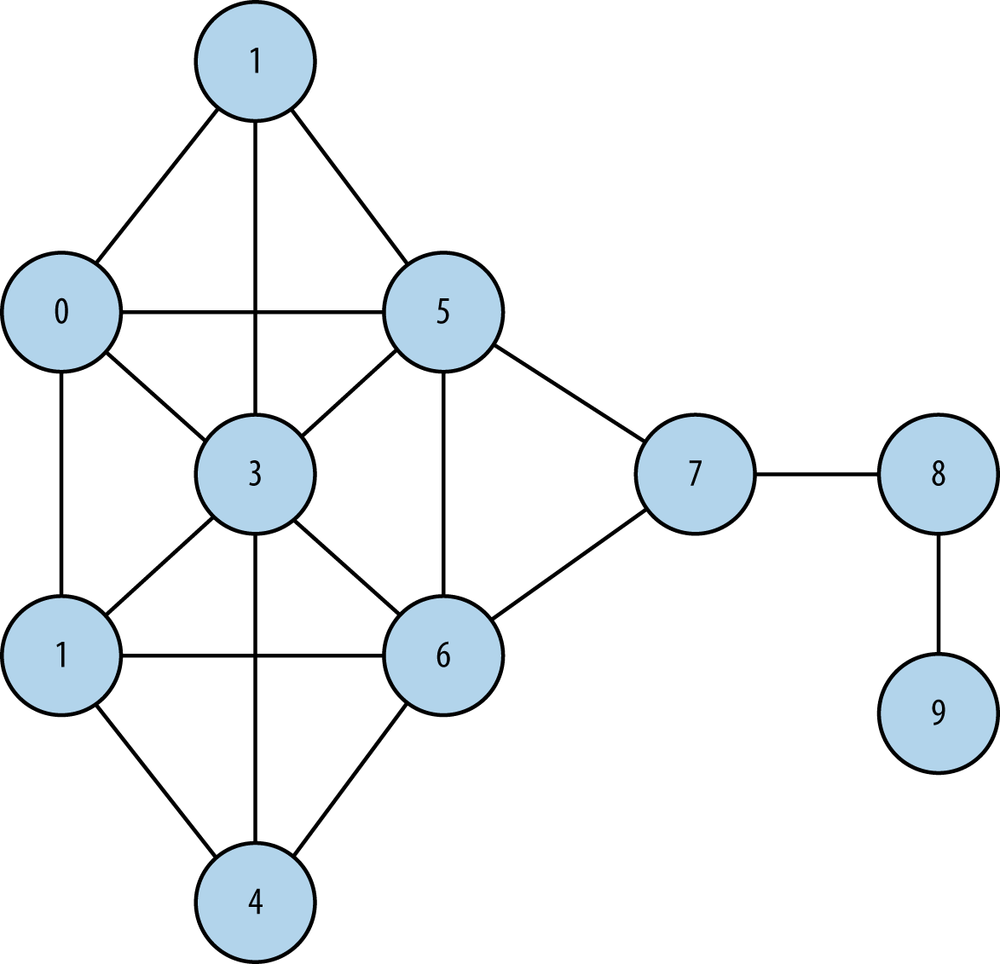
Figure 7-4 shows the Krackhardt kite graph, a well-studied graph in social network analysis that illustrates the differences among the centrality measures introduced in this section. It’s called a “kite graph” because when rendered visually, it has the appearance of a kite.
Example 7-7 shows some code that loads
this graph from NetworkX and calculates centrality measures on it, which
are reproduced in Table 7-1. Although it has no
bearing on the calculations, note that this particular graph is commonly
used as a reference in social networking. As such, the edges are not
directed since a connection in a social network implies a mutual
acceptance criteria. In NetworkX, it is an instance of networkx.Graph as opposed to networkx.DiGraph.
fromoperatorimportitemgetterfromIPython.displayimportHTMLfromIPython.core.displayimportdisplaydisplay(HTML('<img src="files/resources/ch07-github/kite-graph.png" width="400px">'))# The classic Krackhardt kite graphkkg=nx.generators.small.krackhardt_kite_graph()"Degree Centrality"sorted(nx.degree_centrality(kkg).items(),key=itemgetter(1),reverse=True)"Betweenness Centrality"sorted(nx.betweenness_centrality(kkg).items(),key=itemgetter(1),reverse=True)"Closeness Centrality"sorted(nx.closeness_centrality(kkg).items(),key=itemgetter(1),reverse=True)
| Node | Degree centrality | Betweenness centrality | Closeness centrality |
| 0 | 0.44 | 0.02 | 0.53 |
| 1 | 0.44 | 0.02 | 0.53 |
| 2 | 0.33 | 0.00 | 0.50 |
| 3 | 0.67 | 0.10 | 0.60 |
| 4 | 0.33 | 0 | 0.50 |
| 5 | 0.55 | 0.2 | 0.64 |
| 6 | 0.55 | 0.2 | 0.64 |
| 7 | 0.33 | 0.39 | 0.60 |
| 8 | 0.22 | 0.22 | 0.43 |
| 9 | 0.11 | 0.00 | 0.31 |
Spend a few moments studying the Krackhardt kite graph and the centrality measures associated with it before moving on to the next section. These centrality measures will remain in our toolbox moving forward through this chapter.
Extending the Interest Graph with “Follows” Edges for Users
In addition to stargazing and forking repositories, GitHub also features a Twitter-esque notion of “following” other users. In this section, we’ll query GitHub’s API and add “follows” relationships to the graph. Based upon our earlier discussions (such the one in Why Is Twitter All the Rage?) about how Twitter is inherently an interest graph, you know that adding these is basically a way of capturing more interest relationships, since a “following” relationship is essentially the same as an “interested in” relationship.
It’s a good bet that the owner of a repository is likely to be popular within the community that is stargazing at the repository, but who else might be popular in that community? The answer to this question would certainly be an important insight and provide the basis for a useful pivot into further analysis. Let’s answer it by querying GitHub’s User Followers API for the followers of each user in the graph and adding edges to the graph to indicate follows relationships that exist within it. In terms of our graphical model, these additions only insert additional edges into the graph; no new nodes need to be introduced.
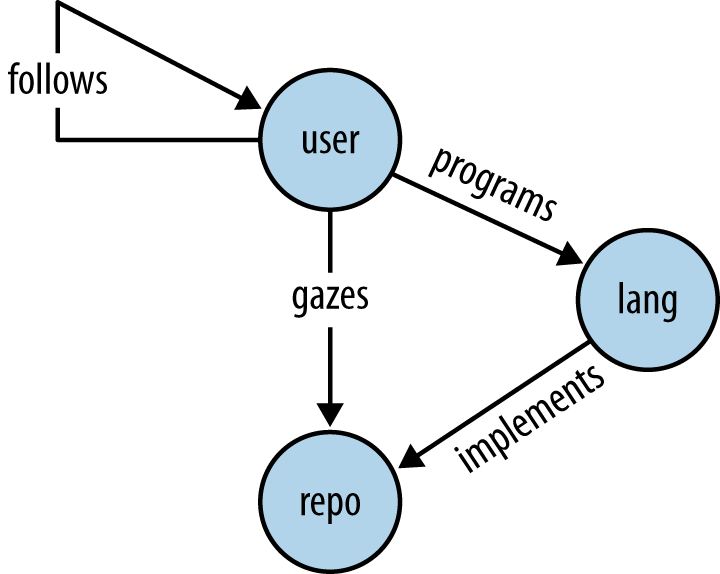
While it would be possible to add all follows relationships that we get back from GitHub to the graph, for now we are limiting our analysis to users who have shown an explicit interest in the repository that is the seed of the graph. Example 7-8 illustrates the sample code that adds following edges to the graph, and Figure 7-5 depicts the updated graph schema that now includes following relationships.
Note
Given GitHub’s authenticated rate limit of 5,000 requests per hour, you would need to make more than 80 requests per minute in order to exceed the rate limit. This is somewhat unlikely given the latency incurred with each request, so no special logic is included in this chapter’s code samples to cope with the rate limit.
# Add (social) edges from the stargazers' followers. This can take a while# because of all of the potential API calls to GitHub. The approximate number# of requests for followers for each iteration of this loop can be calculated as# math.ceil(sg.get_followers() / 100.0) per the API returning up to 100 items# at a time.importsysfori,sginenumerate(stargazers):# Add "follows" edges between stargazers in the graph if any relationships existtry:forfollowerinsg.get_followers():iffollower.login+'(user)'ing:g.add_edge(follower.login+'(user)',sg.login+'(user)',type='follows')exceptException,e:#ssl.SSLError>>sys.stderr,"Encountered an error fetching followers for",\sg.login,"Skipping.">>sys.stderr,e"Processed",i+1," stargazers. Num nodes/edges in graph",\g.number_of_nodes(),"/",g.number_of_edges()"Rate limit remaining",client.rate_limiting
With the incorporation of additional interest data into the graph, the possibilities for analysis become much more interesting. We can now traverse the graph to compute a notion of popularity by counting the number of incoming “follows” edges for a particular user, as demonstrated in Example 7-9. What is so powerful about this analysis is that it enables us to quickly discover who might be the most interesting or influential users to examine for a particular domain of interest.
Given that we seeded the graph with the Mining-the-Social-Web repository, a plausible hypothesis is that users who are interested in this topic may have some affiliation or interest in data mining, and might even have an interest in the Python programming language since its code base is mostly written in Python. Let’s explore whether the most popular users, as calculated by Example 7-9, have any affiliation with this programming language.
fromoperatorimportitemgetterfromcollectionsimportCounter# Let's see how many social edges we added since last time.nx.info(g)# The number of "follows" edges is the differencelen([eforeing.edges_iter(data=True)ife[2]['type']=='follows'])# The repository owner is possibly one of the more popular users in this graph.len([eforeing.edges_iter(data=True)ife[2]['type']=='follows'ande[1]=='ptwobrussell(user)'])# Let's examine the number of adjacent edges to each nodesorted([nforning.degree_iter()],key=itemgetter(1),reverse=True)[:10]# Consider the ratio of incoming and outgoing edges for a couple of users with# high node degrees...# A user who follows many but is not followed back by many.len(g.out_edges('hcilab(user)'))len(g.in_edges('hcilab(user)'))# A user who is followed by many but does not follow back.len(g.out_edges('ptwobrussell(user)'))len(g.in_edges('ptwobrussell(user)'))c=Counter([e[1]foreing.edges_iter(data=True)ife[2]['type']=='follows'])popular_users=[(u,f)for(u,f)inc.most_common()iff>1]"Number of popular users",len(popular_users)"Top 10 popular users:",popular_users[:10]
Sample output follows:
Name:Type:DiGraphNumberofnodes:852Numberofedges:1417Averageindegree:1.6631Averageoutdegree:1.663156689[(u'Mining-the-Social-Web(repo)',851),(u'hcilab(user)',121),(u'ptwobrussell(user)',90),(u'kennethreitz(user)',88),(u'equus12(user)',71),(u'hammer(user)',16),(u'necolas(user)',16),(u'japerk(user)',15),(u'douglas(user)',11),(u'jianxioy(user)',11)]1183189Numberofpopularusers95Top10popularusers:[(u'ptwobrussell(user)',89),(u'kennethreitz(user)',84),(u'necolas(user)',15),(u'japerk(user)',14),(u'hammer(user)',13),(u'isnowfy(user)',6),(u'kamzilla(user)',6),(u'acdha(user)',6),(u'tswicegood(user)',6),(u'albertsun(user)',5)]
As we might have guessed, the owner of the repository that
seeded the original interest graph, ptwobrussell, is the most popular
user in the graph, but another user (kennethreitz) is close with 84
followers, and there are several other users in the top 10 with a
nontrivial number of followers. Among other things, it turns out that
kennethreitz is the author of
the popular requests Python package
that has been used throughout this book. We also see that hcilab is a
user who follows many users but is not followed back by many users.
(We’ll return to this latter observation in a moment.)
Application of centrality measures
Before we do any additional work, let’s save a view of our graph so that we have a stable snapshot of our current state in case we’d like to tinker with the graph and recover it later, or in case we’d like to serialize and share the data. Example 7-10 demonstrates how to save and restore graphs using NetworkX’s built-in pickling capabilities.
# Save your work by serializing out (pickling) the graphnx.write_gpickle(g,"resources/ch07-github/data/github.gpickle.1")# How to restore the graph...# import networkx as nx# g = nx.read_gpickle("resources/ch07-github/data/github.gpickle.1")
With a backup of our work saved out to disk, let’s now apply
the centrality measures from the previous section to this graph and
interpret the results. Since we know that Mining-the-Social-Web(repo) is a
supernode in the graph and connects the majority
of the users (all of them in this case), we’ll remove it from the
graph to get a better view of the network dynamics that might be at
play. This leaves behind only GitHub users and the “follows” edges
between them. Example 7-11 illustrates some
code that provides a starting point for analysis.
fromoperatorimportitemgetter# Create a copy of the graph so that we can iteratively mutate the copy# as needed for experimentationh=g.copy()# Remove the seed of the interest graph, which is a supernode, in order# to get a better idea of the network dynamicsh.remove_node('Mining-the-Social-Web(repo)')# XXX: Remove any other nodes that appear to be supernodes.# Filter any other nodes that you can by threshold# criteria or heuristics from inspection.# Display the centrality measures for the top 10 nodesdc=sorted(nx.degree_centrality(h).items(),key=itemgetter(1),reverse=True)"Degree Centrality"dc[:10]bc=sorted(nx.betweenness_centrality(h).items(),key=itemgetter(1),reverse=True)"Betweenness Centrality"bc[:10]"Closeness Centrality"cc=sorted(nx.closeness_centrality(h).items(),key=itemgetter(1),reverse=True)cc[:10]
Sample results follow:
DegreeCentrality[(u'hcilab(user)',0.1411764705882353),(u'ptwobrussell(user)',0.10470588235294116),(u'kennethreitz(user)',0.10235294117647058),(u'equus12(user)',0.08235294117647059),(u'hammer(user)',0.01764705882352941),(u'necolas(user)',0.01764705882352941),(u'japerk(user)',0.016470588235294115),(u'douglas(user)',0.011764705882352941),(u'jianxioy(user)',0.011764705882352941),(u'mt3(user)',0.010588235294117647)]BetweennessCentrality[(u'hcilab(user)',0.0011790110626111459),(u'douglas(user)',0.0006983995011432135),(u'kennethreitz(user)',0.0005637543592230768),(u'frac(user)',0.00023557126030624264),(u'equus12(user)',0.0001768269145113876),(u'acdha(user)',0.00015935702903069354),(u'hammer(user)',6.654723137782793e-05),(u'mt3(user)',4.988567865308668e-05),(u'tswicegood(user)',4.74606803852283e-05),(u'stonegao(user)',4.068058318733853e-05)]ClosenessCentrality[(u'hcilab(user)',0.14537589026642048),(u'equus12(user)',0.1161965001054185),(u'gawbul(user)',0.08657147291634332),(u'douglas(user)',0.08576408341114222),(u'frac(user)',0.059923888224421004),(u'brunojm(user)',0.05970317408731448),(u'empjustine(user)',0.04591901349775037),(u'jianxioy(user)',0.012592592592592593),(u'nellaivijay(user)',0.012066365007541477),(u'mt3(user)',0.011029411764705881)]
As in our previous analysis, the users ptwobrussell and kennethreitz appear near the top of the list for degree centrality, as expected. However, the hcilab user appears at the top of the chart for all centrality measures. Recalling from our previous analysis that the hcilab user follows lots of other users, a review of this user’s public profile at https://github.com/hcilab suggests that this is an account that may be used as part of a data mining process itself! It is named “Account for Github research” and has only logged one day of activity on GitHub in the previous year. Because this user qualifies as a supernode based on our previous analysis, removing it from the graph and rerunning the centrality measures will likely change the network dynamics and add some clarity to the analysis exercise.
Another observation is that the closeness centrality and degree centrality are much higher than the betweenness centrality, which is virtually at a value of zero. In the context of “following” relationships, this means that no user in the graph is effectively acting as a bridge in connecting other users in the graph. This makes sense because the original seed of the graph was a repository, which provided a common interest. While it would have been worthwhile to discover that there was a user whose betweenness had a meaningful value, it is not all that unexpected that this was not the case. Had the basis of the interest graph been a particular user, the dynamics might have turned out to be different.
Finally, observe that while ptwobrussell and kennethreitz are popular users in the graph, they do not appear in the top 10 users for closeness centrality. Several other users do appear, have a nontrivial value for closeness, and would be interesting to examine. At the time of this writing in August 2013, the user equus12 has over 400 followers but only two forked repositories and no public activity recently. User gawbul has 44 followers, many active repositories, and a fairly active profile. Further examination of the users with the highest degree and closeness centralities is left as an independent exercise. Keep in mind that the dynamic will vary from community to community.
Note
A worthwhile exercise would be to compare and contrast the network dynamics of two different communities, such as the Ruby on Rails community and the Django community. You might also try comparing the dynamics of a Microsoft-centric community versus a Linux-oriented community.
Adding more repositories to the interest graph
All in all, nothing all that interesting turned up in our analysis of the “follows” edges in the graph, which isn’t all that surprising when we recall that the seed of the interest graph was a repository that drew in disparate users from all over the world. What might be worthwhile as a next step would be trying to find additional interests for each user in the graph by iterating over them and adding their starred repositories to the graph. Adding these starred repositories would give us at least two valuable pieces of insight: what other repositories are engaging to this community that is grounded in social web mining (and, to a lesser degree, Python), and what programming languages are popular among this community, given that GitHub attempts to index repositories and determine the programming languages used.
The process of adding repositories and “gazes” edges to the graph is just a simple extension of our previous work in this chapter. GitHub’s “List repositories being starred” API makes it easy enough to get back the list of repositories that a particular user has starred, and we’ll just iterate over these results and add the same kinds of nodes and edges to the graph that we added earlier in this chapter. Example 7-12 illustrates the sample code for making this happen. It adds a significant amount of data to the in-memory graph and can take a while to execute. A bit of patience is required if you’re working with a repository with more than a few dozen stargazers.
# Let's add each stargazer's additional starred repos and add edges# to find additional interests.MAX_REPOS=500fori,sginenumerate(stargazers):sg.logintry:forstarredinsg.get_starred()[:MAX_REPOS]:# Slice to avoid supernodesg.add_node(starred.name+'(repo)',type='repo',lang=starred.language,\owner=starred.owner.login)g.add_edge(sg.login+'(user)',starred.name+'(repo)',type='gazes')exceptException,e:#ssl.SSLError:"Encountered an error fetching starred repos for",sg.login,"Skipping.""Processed",i+1,"stargazers' starred repos""Num nodes/edges in graph",g.number_of_nodes(),"/",g.number_of_edges()"Rate limit",client.rate_limiting
One subtle concern with constructing this graph is that while most users have starred a “reasonable” number of repositories, some users may have starred an extremely high number of repositories, falling far outside statistical norms and introducing a highly disproportionate number of edges and nodes to the graph. As previously noted, a node with an extreme number of edges that is an outlier by a large margin is called a supernode. It is usually not desirable to model graphs (especially in-memory graphs such as the ones implemented by NetworkX) with supernodes because at best they can significantly complicate traversals and other analytics, and at worst they can cause out-of-memory errors. Your particular situation and objectives will determine whether it’s appropriate for you to include supernodes.
A reasonable option that we employ to avoid introducing
supernodes into the graph with Example 7-12 is to
simply cap the number of repositories that we’ll consider for a user.
In this particular case, we limit the number of repositories under
consideration to a fairly high number (500) by slicing the results of
the values being iterated over in the for loop as get_starred()[:500]. Later, if we’re
interested in revisiting the supernodes, we’ll need to query our graph
only for nodes that have a high number of outgoing edges in order to
discover them.
Warning
Python, including the IPython Notebook server kernel, will use as much memory as required as you continue adding data to the graph. If you attempt to create a large enough graph that your operating system can no longer function, a kernel supervisor process may kill the offending Python process. See “Monitoring and Debugging Memory Usage with Vagrant and IPython Notebook” in the online version of Appendix C for some information on how to monitor and increase the memory use of IPython Notebook.
With a graph now constructed that contains additional repositories, we can start having some real fun in querying the graph. There are a number of questions we could now ask and answer beyond the calculation of simple statistics to update us on the overall size of the graph—it might be interesting to zoom in on the user who owns the most repositories that are being watched, for example. Perhaps one of the most pressing questions is what the most popular repositories in the graph are, besides the repository that was used to seed the original interest graph. Example 7-13 demonstrates a sample block of code that answers this question and provides a starting point for further analysis.
Note
Several other useful properties come back from PyGithub’s get_starred API call (a wrapper around
GitHub’s “List repositories being
starred” API) that you might want to consider for future
experiments. Be sure to review the API docs so that you don’t miss
out on anything that might be of use to you in exploring this
space.
# Poke around: how to get users/reposfromoperatorimportitemgetternx.info(g)# Get a list of repositories from the graph.repos=[nforning.nodes_iter()ifg.node[n]['type']=='repo']# Most popular repos"Popular repositories"sorted([(n,d)for(n,d)ing.in_degree_iter()ifg.node[n]['type']=='repo'],\key=itemgetter(1),reverse=True)[:10]# Projects gazed at by a user"Respositories that ptwobrussell has bookmarked"[(n,g.node[n]['lang'])forning['ptwobrussell(user)']ifg['ptwobrussell(user)'][n]['type']=='gazes']# Programming languages for each user"Programming languages ptwobrussell is interested in"list(set([g.node[n]['lang']forning['ptwobrussell(user)']ifg['ptwobrussell(user)'][n]['type']=='gazes']))# Find supernodes in the graph by approximating with a high number of# outgoing edges"Supernode candidates"sorted([(n,len(g.out_edges(n)))forning.nodes_iter()ifg.node[n]['type']=='user'andlen(g.out_edges(n))>500],\key=itemgetter(1),reverse=True)
Sample output follows:
Name:Type:DiGraphNumberofnodes:48857Numberofedges:116439Averageindegree:2.3833Averageoutdegree:2.3833Popularrepositories[(u'Mining-the-Social-Web(repo)',851),(u'bootstrap(repo)',273),(u'd3(repo)',194),(u'dotfiles(repo)',166),(u'node(repo)',139),(u'storm(repo)',139),(u'impress.js(repo)',125),(u'requests(repo)',122),(u'html5-boilerplate(repo)',114),(u'flask(repo)',106)]Respositoriesthatptwobrussellhasbookmarked[(u'Legal-Forms(repo)',u'Python'),(u'python-linkedin(repo)',u'Python'),(u'ipython(repo)',u'Python'),(u'Tweet-Relevance(repo)',u'Python'),(u'PyGithub(repo)',u'Python'),(u'Recipes-for-Mining-Twitter(repo)',u'JavaScript'),(u'wdb(repo)',u'JavaScript'),(u'networkx(repo)',u'Python'),(u'twitter(repo)',u'Python'),(u'envoy(repo)',u'Python'),(u'Mining-the-Social-Web(repo)',u'JavaScript'),(u'PayPal-APIs-Up-and-Running(repo)',u'Python'),(u'storm(repo)',u'Java'),(u'PyStratus(repo)',u'Python'),(u'Inquire(repo)',u'Python')]Programminglanguagesptwobrussellisinterestedin[u'Python',u'JavaScript',u'Java']Supernodecandidates[(u'hcilab(user)',614),(u'equus12(user)',569),(u'jianxioy(user)',508),(u'mcroydon(user)',503),(u'umaar(user)',502),(u'rosco5(user)',502),(u'stefaneyr(user)',502),(u'aljosa(user)',502),(u'miyucy(user)',501),(u'zmughal(user)',501)]
An initial observation is that the number of edges in the new graph is three orders of magnitude higher than in the previous graph, and the number of nodes is up well over one order of magnitude. This is where analysis can really get interesting because of the complex network dynamics. However, the complex network dynamics also mean that it will take nontrivial amounts of time for NetworkX to compute global graph statistics. Keep in mind that just because the graph is in memory doesn’t mean that all computation will necessarily be fast. This is where a basic working knowledge of some fundamental computing principles can be helpful.
Computational Considerations
Note
This brief section contains a somewhat advanced discussion that involves some of the mathematical complexity involved in running graph algorithms. You are encouraged to read it, though you could opt to revisit this later if this is your first reading of this chapter.
For the three centrality measures being computed, we know that the calculation of degree centrality is relatively simple and should be fast, requiring little more than a single pass over the nodes to compute the number of incident edges. Both betweenness and closeness centralities, however, require computation of the minimum spanning tree. The underlying NetworkX minimum spanning tree algorithm implements Kruskal’s algorithm, which is a staple in computer science education. In terms of runtime complexity, it takes on the order of O(E log E), where E represents the number of edges in the graph. Algorithms of this complexity are generally considered efficient, but 100,000 * log(100,000) is still approximately equal to one million operations, so a full analysis can take some time.
The removal of supernodes is critical in achieving reasonable runtimes for network algorithms, and a targeted exploration in which you extract a subgraph of interest for more thorough analysis is an option to consider. For example, you may want to selectively prune users from the graph based upon filtering criteria such as their number of followers, which could provide a basis for judging their importance to the overall network. You might also consider pruning repositories based upon a threshold for a minimum number of stargazers.
When conducting analyses on large graphs, you are advised to examine each of the centrality measures one at a time so that you can more quickly iterate on the results. It is also critical to remove supernodes from the graph in order to achieve reasonable runtimes, since supernodes can easily dominate computation in network algorithms. Depending on the size of your graph, this may also be a situation in which increasing the amount of memory available to your virtual machine could be beneficial. See Appendix C for details on memory profiling and configuration with Vagrant.
Using Nodes as Pivots for More Efficient Queries
Another characteristic of the data to consider is the popularity of programming languages that are employed by users. It could be the case that users star projects that are implemented in programming languages that they are at least loosely interested in and able to use themselves. Although we have the data and the tools to analyze users and popular programming languages with our existing graph, our schema currently has a shortcoming. Since a programming language is modeled as an attribute on a repository, it is necessary to scan all of the repository nodes and either extract or filter by this attribute in order to answer nontrivial questions.
For example, if we wanted to know which programming languages a
user programs in using the current schema, we’d need to look up all of
the repositories that user gazes at, extract the lang properties, and compute a frequency
distribution. This doesn’t seem too cumbersome, but what if we wanted to
know how many users program in a particular programming language?
Although the answer is computable with the existing schema, it requires
a scan of every repository node and a count of all of the incoming
“gazes” edges. With a modification to the graph schema, however,
answering this question could be as simple as accessing a single node in
the graph. The modification would involve creating a node in the graph
for each programming language that has incoming programs edges that connect users who program
in that language, and outgoing implements edges that connect
repositories.
Figure 7-6 illustrates our final graph schema, which incorporates programming languages as well as edges between users, repositories, and programming languages. The overall effect of this schema change is that we’ve taken a property of one node and created an explicit relationship in the graph that was previously implicit. From the standpoint of completeness, there is no new data, but the data that we do have can now be computed on more efficiently for certain queries. Although the schema is fairly simple, the universe of possible graphs adhering to it that could be easily constructed and mined for valuable knowledge is immense.
The nice thing about having a single node in the graph that corresponds to a programming language, as opposed to representing a programming language as a property on many nodes, is that a single node acts as a natural point of aggregation. Central points of aggregation can greatly simplify many kinds of queries, such as finding maximal cliques in the graph, as described in Analyzing mutual friendships with directed graphs. For example, finding the maximal clique of users who all follow one another and program with a particular language can be more efficiently computed with NetworkX’s clique detection algorithms since the requirement of a particular programming language node in the clique significantly constrains the search.
Example 7-14 introduces some sample code that constructs the updates as depicted in the final graph schema. Because all of the information that we need to construct the additional nodes and edges is already present in the existing graph (since we have already stored the programming language as a property on the repository nodes), no additional requests to the GitHub API are necessary.
# Iterate over all of the repos, and add edges for programming languages# for each person in the graph. We'll also add edges back to repos so that# we have a good point to "pivot" upon.repos=[nforning.nodes_iter()ifg.node[n]['type']=='repo']forrepoinrepos:lang=(g.node[repo]['lang']or"")+"(lang)"stargazers=[ufor(u,r,d)ing.in_edges_iter(repo,data=True)ifd['type']=='gazes']forsginstargazers:g.add_node(lang,type='lang')g.add_edge(sg,lang,type='programs')g.add_edge(lang,repo,type='implements')
Our final graph schema is capable of answering a variety of questions. A few questions that seem ripe for investigation at this point include:
Which languages do particular users program with?
How many users program in a particular language?
Which users program in multiple languages, such as Python and JavaScript?
Which programmer is the most polyglot (programs with the most languages)?
Is there a higher correlation between particular languages? (For example, given that a programmer programs in Python, is it more likely that this same programmer also programs in JavaScript or with Go based upon the data in this graph?)
Example 7-15 provides some sample code that is a good starting point for answering most of these questions, and others like them.
# Some statsnx.info(g)# What languages exist in the graph?[nforning.nodes_iter()ifg.node[n]['type']=='lang']# What languages do users program with?[nforning['ptwobrussell(user)']ifg['ptwobrussell(user)'][n]['type']=='programs']# What is the most popular programming language?"Most popular languages"sorted([(n,g.in_degree(n))forning.nodes_iter()ifg.node[n]['type']=='lang'],key=itemgetter(1),reverse=True)[:10]# How many users program in a particular language?python_programmers=[ufor(u,l)ing.in_edges_iter('Python(lang)')ifg.node[u]['type']=='user']"Number of Python programmers:",len(python_programmers)javascript_programmers=[ufor(u,l)ing.in_edges_iter('JavaScript(lang)')ifg.node[u]['type']=='user']"Number of JavaScript programmers:",len(javascript_programmers)# What users program in both Python and JavaScript?"Number of programmers who use JavaScript and Python"len(set(python_programmers).intersection(set(javascript_programmers)))# Programmers who use JavaScript but not Python"Number of programmers who use JavaScript but not Python"len(set(javascript_programmers).difference(set(python_programmers)))# XXX: Can you determine who is the most polyglot programmer?
Sample output follows:
Name:
Type: DiGraph
Number of nodes: 48952
Number of edges: 174180
Average in degree: 3.5582
Average out degree: 3.5582
[u'PHP(lang)', u'Clojure(lang)', u'ActionScript(lang)', u'Logtalk(lang)',
u'Scilab(lang)', u'Processing(lang)', u'D(lang)', u'Pure Data(lang)',
u'Java(lang)', u'SuperCollider(lang)', u'Julia(lang)', u'Shell(lang)',
u'Haxe(lang)', u'Gosu(lang)', u'JavaScript(lang)', u'CLIPS(lang)',
u'Common Lisp(lang)', u'Visual Basic(lang)', u'Objective-C(lang)',
u'Delphi(lang)', u'Objective-J(lang)', u'PogoScript(lang)',
u'Scala(lang)', u'Smalltalk(lang)', u'DCPU-16 ASM(lang)',
u'FORTRAN(lang)', u'ASP(lang)', u'XML(lang)', u'Ruby(lang)',
u'VHDL(lang)', u'C++(lang)', u'Python(lang)', u'Perl(lang)',
u'Assembly(lang)', u'CoffeeScript(lang)', u'Racket(lang)',
u'Groovy(lang)', u'F#(lang)', u'Opa(lang)', u'Fantom(lang)',
u'Eiffel(lang)', u'Lua(lang)', u'Puppet(lang)', u'Mirah(lang)',
u'XSLT(lang)', u'Bro(lang)', u'Ada(lang)', u'OpenEdge ABL(lang)',
u'Fancy(lang)', u'Rust(lang)', u'C(lang)', '(lang)', u'XQuery(lang)',
u'Vala(lang)', u'Matlab(lang)', u'Apex(lang)', u'Awk(lang)', u'Lasso(lang)',
u'OCaml(lang)', u'Arduino(lang)', u'Factor(lang)', u'LiveScript(lang)',
u'AutoHotkey(lang)', u'Haskell(lang)', u'HaXe(lang)', u'DOT(lang)',
u'Nu(lang)', u'VimL(lang)', u'Go(lang)', u'ABAP(lang)', u'ooc(lang)',
u'TypeScript(lang)', u'Standard ML(lang)', u'Turing(lang)', u'Coq(lang)',
u'ColdFusion(lang)', u'Augeas(lang)', u'Verilog(lang)', u'Tcl(lang)',
u'Nimrod(lang)', u'Elixir(lang)',u'Ragel in Ruby Host(lang)', u'Monkey(lang)',
u'Kotlin(lang)', u'C#(lang)',u'Scheme(lang)', u'Dart(lang)', u'Io(lang)',
u'Prolog(lang)', u'Arc(lang)', u'PowerShell(lang)', u'R(lang)',
u'AppleScript(lang)', u'Emacs Lisp(lang)', u'Erlang(lang)']
[u'JavaScript(lang)', u'Java(lang)', u'Python(lang)']
Most popular languages
[(u'JavaScript(lang)', 851), (u'Python(lang)', 715), ('(lang)', 642),
(u'Ruby(lang)', 620), (u'Java(lang)', 573), (u'C(lang)', 556),
(u'C++(lang)', 508), (u'PHP(lang)', 477), (u'Shell(lang)', 475),
(u'Objective-C(lang)', 435)]
Number of Python programmers: 715
Number of JavaScript programmers: 851
Number of programmers who use JavaScript and Python
715
Number of programmers who use JavaScript but not Python
136Although the graph schema is conceptually simple, the number of
edges has increased by nearly 50% because of the additional programming
language nodes! As we see from the output for a few sample queries,
there are quite a large number of programming languages in use, and
JavaScript and Python top the list. The primary source code for the
original repository of interest is written in Python, so the emergence
of JavaScript as a more popular programming language among users may be
indicative of a web development audience. Of course, it is also the case
that JavaScript is just a popular programming language, and there is
often a high correlation between JavaScript for a client-side language
and Python as a server-side language. Ruby is also a popular programming
language and is commonly used for server-side web development. It
appears fourth in the list. The appearance of '(lang)' as the third most popular language is
an indication that there are 642 repositories to which GitHub could not
assign a programming language, and in aggregate, they rolled up into
this single category.
The possibilities are immense for analyzing a graph that expresses
people’s interests in other people, open source projects in
repositories, and programming languages. Whatever analysis you choose to
do, think carefully about the nature of the problem and extract only the
relevant data from the graph for analysis—either by zeroing in on a set
of nodes to extract with NetworkX graph’s subgraph method, or by filtering out nodes by
type or frequency threshold.
Note
A bipartite analysis of users and programming languages would likely be a worthwhile endeavor, given the nature of the relationship between users and programming languages. A bipartite graph involves two disjoint sets of vertices that are connected by edges between the sets. You could easily remove repository nodes from the graph at this point to drastically enhance the efficiency of computing global graph statistics (the number of edges would decrease by over 100,000).
Visualizing Interest Graphs
Although it is exciting to visualize a graph, and a picture really is often worth far more than a thousand words, keep in mind that not all graphs are easily visualized. However, with a little bit of thought you can often extract a subgraph that can be visualized to the extent that it provides some insight or intuition into the problem that you are trying to solve. As you know from our work in this chapter, a graph is just a type of data structure and has no definite visual rendering. To be visualized, a particular type of layout algorithm must be applied that maps the nodes and edges to a two- or three-dimensional space for visual consumption.
We’ll stick to the core toolkit that we’ve used throughout the book and lean on NetworkX’s ability to export JSON that can be rendered by the JavaScript toolkit D3, but there are many other toolkits that you could consider when visualizing graphs. Graphviz is a highly configurable and rather classic tool that can lay out very complex graphs as bitmap images. It has traditionally been used in a terminal setting like other command-line tools, but it also now ships with a user interface for most platforms. Another option is Gephi, another popular open source project that provides some powerful interactive possibilities; Gephi has rapidly grown in popularity over the past few years and is an option that’s well worth your consideration.
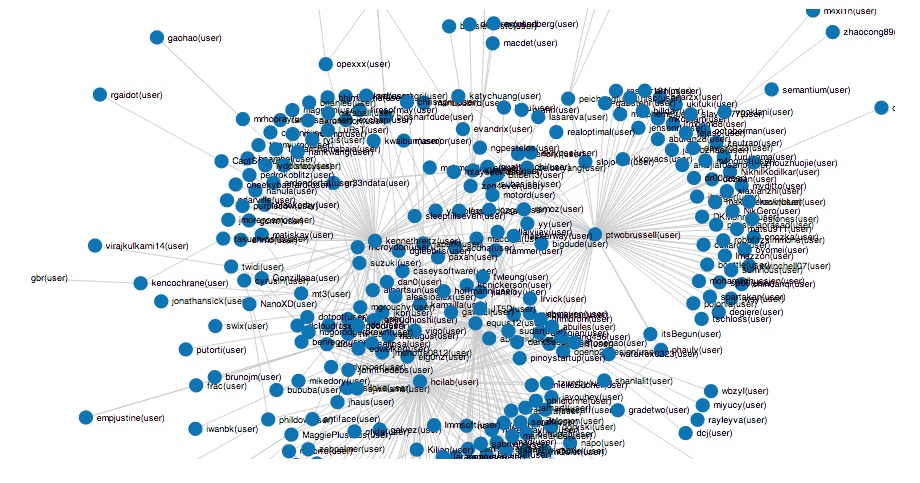
Example 7-16 illustrates a template for extracting a subgraph of the users who gaze at the seed of our original graph (the Mining-the-Social-Web repository) and the “following” connections among them. It extracts the users in the graph with a common interest and visualize the “follows” edges among them. Keep in mind that the entire graph as constructed in this chapter is quite large and contains tens of thousands of nodes and hundreds of thousands of edges, so you’d need to spend some time better understanding it in order to achieve a reasonable visualization with a tool like Gephi.
importosimportjsonfromIPython.displayimportIFramefromIPython.core.displayimportdisplayfromnetworkx.readwriteimportjson_graph"Stats on the full graph"nx.info(g)# Create a subgraph from a collection of nodes. In this case, the# collection is all of the users in the original interest graphmtsw_users=[nforningifg.node[n]['type']=='user']h=g.subgraph(mtsw_users)"Stats on the extracted subgraph"nx.info(h)# Visualize the social network of all people from the original interest graph.d=json_graph.node_link_data(h)json.dump(d,open('resources/ch07-github/force.json','w'))# IPython Notebook can serve files and display them into# inline frames. Prepend the path with the 'files' prefix.# A D3 template for displaying the graph data.viz_file='files/resources/ch07-github/force.html'# Display the D3 visualization.display(IFrame(viz_file,'100%','600px'))
Figure 7-7 shows sample results of running this example code.
Closing Remarks
Note
The source code outlined for this chapter and all other chapters is available at GitHub in a convenient IPython Notebook format that you’re highly encouraged to try out from the comfort of your own web browser.
Although various sorts of graphs have been sprinkled throughout earlier chapters in this book, this chapter provided a more substantial introduction to their use as a flexible data structure for representing a network of GitHub users and their common interests in certain software project repositories and programming languages. GitHub’s rich API and NetworkX’s easy-to-use API are a nice duo for mining some fascinating and often-overlooked social web data in one of the most overtly “social” web properties that’s in widespread use across the globe. The notion of an interest graph isn’t an entirely new idea, but its application to the social web is a fairly recent development with exciting implications. Whereas interest graphs (or comparable representations) have been used by advertisers to effectively place ads for some time, they’re now being used by entrepreneurs and software developers to more effectively target interests and make intelligent recommendations that enhance a product’s relevance to users.
Like most of the other chapters in the book, this chapter has served as merely a primer for graphical modeling, interest graphs, GitHub’s API, and what you can do with these technologies. You could just as easily apply the graphical modeling techniques in this chapter to other social web properties such as Twitter or Facebook and achieve compelling analytic results, as well as applying other forms of analysis to the rich data that’s available from GitHub’s API. The possibilities, as always, are quite vast. My hope first and foremost is that you’ve enjoyed yourself while working through the exercises in this chapter and learned something new that you can take with you throughout your social web mining journey and beyond.
Recommended Exercises
- Repeat the exercises in this chapter, but use a different repository as a starting point. Do the findings from this chapter generally hold true, or are the results of your experiments different in any particular way?
- GitHub has published some data regarding correlations between programming languages. Review and explore the data. Is it any different from what you could collect with the GitHub API?
- NetworkX provides an extensive collection of graph traversal algorithms. Review the documentation and pick a couple of algorithms to run on the data. Centrality measures, cliques, and bipartite algorithms might make a good starting point for inspiration. Can you compute the largest clique of users in the graph? What about the largest clique that shares a common interest, such as a particular programming language?
- The GitHub Archive provides an extensive amount of data about GitHub activity at a global level. Investigate this data, using some of the recommended “big data” tools to explore it.
- Compare data points across two similar GitHub projects. Given the inextricable links between Mining-the-Social-Web and Mining-the-Social-Web-2nd-Edition, these two projects make for a suitable starting point for analysis. Who has bookmarked or forked one but not the other? How do the interest graphs compare? Can you build and analyze an interest graph that contains all of the users who are interested in both editions?
- Use a similarity measurement such as Jaccard similarity (see
nltk.metrics.jaccard_distance; see also Contingency tables and scoring functions) to compute the similarity of two arbitrary users on GitHub based upon features such as starred repositories in common, programming languages in common, and other features that you can find in GitHub’s API. - Given users and existing interests, can you design an algorithm that recommends interests for other users? Consider adapting the code from A Whiz-Bang Introduction to TF-IDF that uses cosine similarity as a means of predicting relevance.
- Employ a histogram to gain insight into a facet of the interest graph in this chapter, such as the popularity of programming languages.
- Explore graph visualization tools like Graphviz and Gephi to lay out and render a graph for visual inspection.
You may have heard that Google discontinued its Google Reader product in mid-2013. One of the ensuing discussions around the perceived void it left is whether a subscription graph, a more decentralized version of subscription-oriented content based upon “following” mechanics, is already emerging all around us. Do you think that the future of the Web largely involves a technological paradigm shift that makes it easy to unite people with common interests? Is it already happening?
Explore the Friendster social network and ground-truth communities data set and use NetworkX algorithms to analyze it.
Online Resources
The following list of links from this chapter may be useful for review:
[27] A more abstract version of a graph called a hypergraph contains hyperedges that can connect an arbitrary number of vertices.
[28] In the current discussion, the term “energy” is used to generically describe flow within an abstract graph.
Get Mining the Social Web, 2nd Edition now with the O’Reilly learning platform.
O’Reilly members experience books, live events, courses curated by job role, and more from O’Reilly and nearly 200 top publishers.