11.7 COMPARING MOVING OBJECT TRAJECTORIES
11.7.1 Distance Between Trajectories
To perform clustering or similarity searches on trajectories of moving objects, an appropriate definition of the distance (or similarity) between two trajectories is important. Typically, the trajectory of a moving object is represented as a sequence of consecutive locations in a two- or three-dimensional space, in contrast to the one-dimensional case, which is common in timeseries databases [33, 52]. In addition, distances for moving object trajectories should be robust to outliers since measurements in mobile environments are noisy and the movement of objects may contain “gaps.” Some distance measures proposed for moving object trajectories are investigated below.
For example, consider two trajectories of moving objects on the (x, y)-plane given as A = ((ax,1, ay,1),…, (ax,n, ay,n)) and B = ((bx,1, by,1),…, (bx,m, by,m)). Their lengths are n and m, respectively. When n = m, we can apply the Euclidean distance (L2 distance), which is simple and also the most popular:
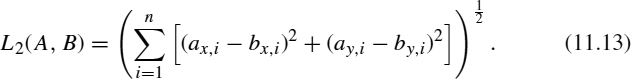
Although the Euclidean distance can be evaluated efficiently, it cannot be applied when two trajectories have different lengths.
11.7.2 Dynamic Time Warping (DTW)
It is often necessary to compute the similarity between two trajectories with different lengths. A well-known approach is to use dynamic time warping (DTW) [33, 52], which is ...
Get Mobile Intelligence now with the O’Reilly learning platform.
O’Reilly members experience books, live events, courses curated by job role, and more from O’Reilly and nearly 200 top publishers.

