Modern Control System Theory and Design, 2nd Edition

2.26.  STATE TRANSITION MATRIX

The state transition matrix relates the state of a system at t = t₀ to its state at a subsequent time t, when the input u(t) = 0. In order to define the state transition matrix of a system, let us consider the general form of the state equation [see Eq. 2.197]:

The Laplace transform of Eq. (2.252) is given by

where X(s) is the Laplace transform of x(t) and U(s) is the Laplace transform of u(t). Solving for X(s), we obtain

The inverse Laplace transform of Eq. (2.254) gives the state transition equation

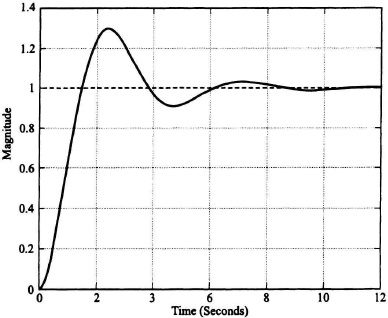
Figure 2.37   Unit step response of system shown in Figure 2.29 obtained using the MATLAB Program in Table 2.12.

where the state transition matrix is defined by

The first term on the right-hand side of Eq. (2.255) is known as the homogeneous solution and is due only to the initial conditions; the second term on the right-hand side of Eq. (2.255), the convolution ...