Modern Control System Theory and Design, 2nd Edition

PROBLEMS

2.1 The periodic function f(t) has the line spectrum shown in Figure P2.1. Assuming that f(t) is an even function, determine the following:

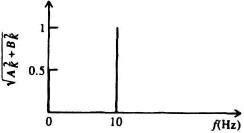
Figure P2.1

(a)  The trigonometric Fourier series for f(t).

(b)  The complex Fourier series for f(t).

2.2. Find v(t) in the circuit of Figure P2.2 using the Laplace transform.

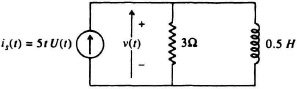
Figure P2.2

2.3. Find x(t) for t0 for

d²x(t)/dt² + x(t) = 0

where x(0) = 1 and dx(0)/dt = −1.

2.4. Consider the Laplace transform

Using the final-value theorem, determine f(∞). Check your answer by finding the inverse Laplace transform f(t) and letting t → ∞.

2.5. The initial conditions for the following differential equation

are given by

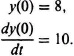
(a)  Write in its simplest form the Laplace transform of the function Y(s), by taking the Laplace transform of this differential equation.

(b)  Expand Y(s) by means of the partial fraction expansion method. Determine all unknown constants. ...