Modern Control System Theory and Design, 2nd Edition

PROBLEMS

8.1. The control system illustrated in Figure P8.1(i) contains linear-state-variable-feedback elements h₁ and h₂.

(a)  Determine the gain K and the linear-state-variable-feedback constants h₁ and h₂ so that the resulting control system represents a zero steady-state step error system and its characteristic equation contains roots at −2 + j, −2 − j, and −8.

Figure P8.1(i)

(b)  The same performance can be obtained as in part (a) if we implement a series controller, G_c(s), instead of using linear-state-variable-feedback as illustrated in the configuration shown in Figure P8.1(ii).

Figure P8.1(ii)

Determine the transfer function of G_c(s) in terms of K, h₁, and h₂ obtained in part (a) and the other system parameters provided.

8.2. A control system containing a controller and a process are illustrated in the block diagram in Figure P8.2(i).

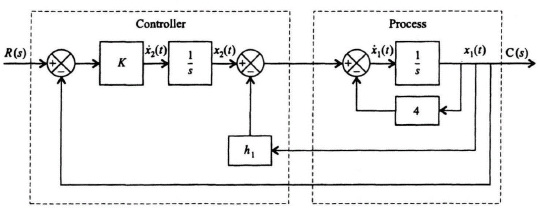
Figure P8.2(i)

(a)  Determine the state equations of this control system.

(b)  Determine the characteristic equation from knowledge of P.

(c)  Determine the constant h₁ and the gain K if the roots of the characteristic equation are at −6 and −8.

(d)  Instead of using the controller configuration, the control-system engineer wishes to design ...