November 2010
Intermediate to advanced
288 pages
8h 34m
English
book
Notes on Digital Signal Processing: Practical Recipes for Design, Analysis and Implementation
by C. Britton Rorabaugh
Content preview from Notes on Digital Signal Processing: Practical Recipes for Design, Analysis and Implementation
Become an O’Reilly member and get unlimited access to this title plus top books and audiobooks from O’Reilly and nearly 200 top publishers, thousands of courses curated by job role, 150+ live events each month,
O’Reilly covers everything we've got, with content to help us build a world-class technology community, upgrade the capabilities and competencies of our teams, and improve overall team performance as well as their engagement.I wanted to learn C and C++, but it didn't click for me until I picked up an O'Reilly book. When I went on the O’Reilly platform, I was astonished to find all the books there, plus live events and sandboxes so you could play around with the technology.I’ve been on the O’Reilly platform for more than eight years. I use a couple of learning platforms, but I'm on O'Reilly more than anybody else. When you're there, you start learning. I'm never disappointed.I'm always learning. So when I got on to O'Reilly, I was like a kid in a candy store. There are playlists. There are answers. There's on-demand training. It's worth its weight in gold, in terms of what it allows me to do.
Note 20. Fast Convolution Using the FFT
Consider an FIR filter having a unit-sample response, h[n], that extends for NR samples. Such a filter’s output, y[k], at time k is given by the discrete convolution
20.1
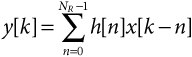
where x[k] is the input sequence. In order to produce a block of NB output samples, y[0] through y[NB – 1], Eq. (20.1) must process a block of NB + NR – 1 input samples from x[–NR + 1] through x[NB – 1]. Assuming that x[k] is valid only for k ≥ 0, the first NR – 1 samples of the output will not be valid because computation of these values depends on samples of x[k] before k = 0. To produce a second block of NB output samples, y[NB] through ...
Become an O’Reilly member and get unlimited access to this title plus top books and audiobooks from O’Reilly and nearly 200 top publishers, thousands of courses curated by job role, 150+ live events each month,
and much more.
Read now
Unlock full access
More than 5,000 organizations count on O’Reilly
O’Reilly covers everything we've got, with content to help us build a world-class technology community, upgrade the capabilities and competencies of our teams, and improve overall team performance as well as their engagement.Julian F.
I wanted to learn C and C++, but it didn't click for me until I picked up an O'Reilly book. When I went on the O’Reilly platform, I was astonished to find all the books there, plus live events and sandboxes so you could play around with the technology.Addison B.
I’ve been on the O’Reilly platform for more than eight years. I use a couple of learning platforms, but I'm on O'Reilly more than anybody else. When you're there, you start learning. I'm never disappointed.Amir M.
I'm always learning. So when I got on to O'Reilly, I was like a kid in a candy store. There are playlists. There are answers. There's on-demand training. It's worth its weight in gold, in terms of what it allows me to do.