Numerical Methods for Engineers and Scientists 3rd Edition

Appendix C

Derivation of the Real Discrete Fourier Transform (DFT)

The discrete Fourier series that approximates the value of a function with a finite number of sine and cosine terms is introduced in Eq. (7.44). The formulas for the coefficients are given in Eqs. (7.45). This Appendix presents the mathematical details of the derivation of the formulas for the coefficients. In Section C.1 the property of orthogonality of sines and cosines over a set of equally spaced discrete points is derived¹, and in Section C.2 it is used for deriving the coefficients that are the real DFT.

C.1 ORTHOGONALITY OF SINES AND COSINES FOR DISCRETE POINTS

The property of orthogonality for equally spaced discrete points over the interval is given by:

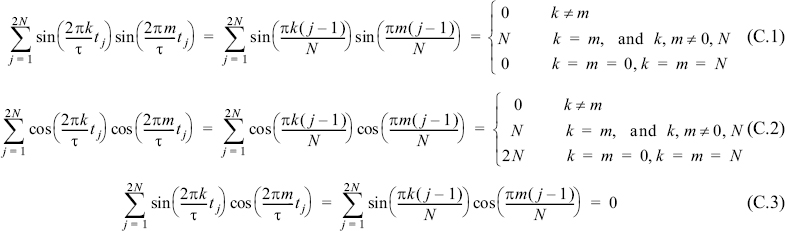
To prove Eqs. (C.1)-(C.3) consider the infinite series where n is an integer. If z = e^πin/N, then this series can be recognized as standard geometric series:

The series in Eq. (C.4) can be written out as: 1 + z + z² + ... + z^{2N − 1}. Multiplying this finite series by (1 − z) (where z ≠ 1) yields:

Thus,

Therefore, the geometric series in Eq. (C.4) converges ...