16.2. Fundamentals of Low-Pass Filters
The most simple low-pass filter is the passive RC low-pass network shown in Fig. 16.2.
Its transfer function is
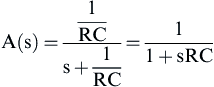
where the complex frequency variable, s = jω + σ, allows for any time variable signals. For pure sine waves, the damping constant, σ, becomes zero and s = jω.
For a normalized presentation of the transfer function, s is referred to the filter's corner frequency, or −3 dB frequency, ωC, and has these relationships:
With the corner frequency of the low-pass in Fig. 16.2 ...
Get Op Amps for Everyone, 5th Edition now with the O’Reilly learning platform.
O’Reilly members experience books, live events, courses curated by job role, and more from O’Reilly and nearly 200 top publishers.

