CAUSAL MODELS
Recall that causal, or associative, models assume that the variable we are trying to forecast is somehow related to other variables in the environment. The forecasting challenge is to discover the relationships between the variable of interest and these other variables. These relationships, which can be very complex, take the form of a mathematical model, which is used to forecast future values of the variable of interest. Some of the best-known causal models are regression models. In this section we look at linear and multiple regression and how they are used in forecasting.
Linear Regression
In linear regression the variable being forecast, called the dependent variable, is related to some other variable, called the independent variable, in a linear (or straightline) way. Figure 8-2 shows how a linear regression line relates to the data. You can see that the dependent variable is linearly related to the independent variable. The relationship between two variables is the equation of a straight line:
![]() Linear regression
Linear regression
Procedure that models a straight-line relationship between two variables.
FIGURE 8-2 Linear regression line fit to historical data
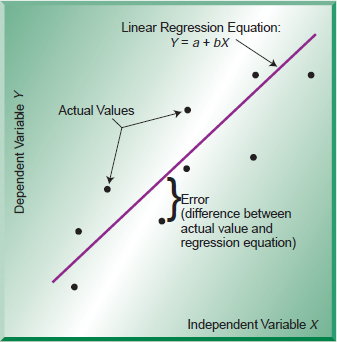
Y = a + bX
where Y = dependent variable
X = independent variable
a = Y intercept of the line
b = slope of the line
Many straight ...
Get Operations Management: An Integrated Approach, 5th Edition now with the O’Reilly learning platform.
O’Reilly members experience books, live events, courses curated by job role, and more from O’Reilly and nearly 200 top publishers.

