Optical Communications, 2nd Edition

5.4 THE ALIGNMENT AND FIELD-MATCHING PROBLEM

In the preceding sections, we considered an idealized heterodyning operation in which both the received field and the local field are perfectly aligned and each generates identical and overlapping diffraction patterns in the focal plane. In practice, it is somewhat difficult to obtain this ideal heterodyning condition, and effects of misalignment and local-field distortion must be considered.

Minimizing these anomalies, therefore, becomes an important part of system design.

Let us reconsider the basic heterodyning equation (5.1.3), when the local and received fields are not identical. Recognizing that the spatial integral is simply a complex number, having a given magnitude and vector angle, the signal term in Eq. (5.1.6) generalizes to

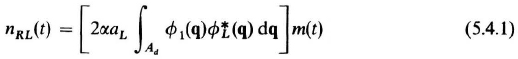
where m(t) is again given by Eq. (5.1.10). Note that the integral magnitude term now becomes a multiplying factor on the signal amplitude. It is convenient to rewrite Eq. (5.4.1) as

where we have introduced the heterodyning amplitude loss factor

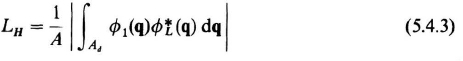
By a simple application of the Schwartz inequality, it can be easily established that L_H ≤ 1, and therefore acts as a true amplitude Joss on the signal term. Thus ...