Principles of Electromagnetic Waves and Materials, 2nd Edition

Appendix 1B: Retarded Potentials and Review of Potentials for the Static Cases

1B.1Electrostatics

The basic equation is

(1B.1)$$\nabla \times E=0.$$

It is known that the curl of the gradient of any scalar is zero, that is,

(1B.2)$$\nabla \times \left[\text{gradient of}\text{any}\text{scalar}\right]\equiv 0.$$

Therefore, E can be expressed as the gradient of a scalar ψ (electrostatic potential).

(1B.3)$$E=-\nabla \mathrm{\psi },$$

where ψ satisfies Poisson’s equation

(1B.4)$${\nabla }^2\mathrm{\psi }=-\frac{{\mathrm{\rho }}_{\text{v}}}{\mathrm{\epsilon }}.$$

The solution of Equation 1B.4 at an arbitrary point P is given by

(1B.5)$$\mathrm{\psi }\left(r\right)={\displaystyle \underset{v^{\prime }}{\iiint }\frac{{\mathrm{\rho }}_{\text{v}}\left(r^{\prime }\right)}{4\mathrm{\pi }\mathrm{\epsilon }\left|r-r^{\prime }\right|}\text{d}{v}^{\prime },}$$

where the volume charge density ρ_v exists over volume v′ as shown in Figure 1B.1.

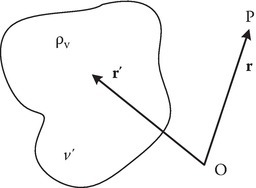
FIGURE 1B.1Electrostatic geometry.

1B.2Magnetostatics

The basic equation ...