Principles of Electromagnetic Waves and Materials, 2nd Edition

Problems

Chapter 1

P1.1For a simple lossless medium, derive the wave equations for E and H.

P1.2Obtain the wave Equations 1.18 and 1.19 subject to the Lorentz condition given by Equation 1.21.

P1.3Obtain Equation 1.27.

P1.4Show that for a time-harmonic case, Equation 1.22 reduces to Equation 1.50.

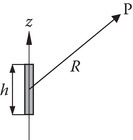
P1.5a.Obtain the expression for the time-harmonic retarded potential A for a current element of small length h located on the z-axis as shown in the figure.

b.Hence obtain the electric and magnetic fields at P. Assume that the current in the filament is I₀(A).

c.In the far zone, that is, for R ≫ λ, h ≪ λ, obtain E , H , E × H, and ⟨S⟩.

P1.6Lecture ...