Probability and Statistics for Finance

Appendix B. Fundamentals of Matrix Operations and Concepts

For several topics in this book, we used principles, concepts, and results from the field of matrix algebra. In this appendix, we provide a review of matrix algebra.

THE NOTION OF VECTOR AND MATRIX

Consider a data series x = {x₁, x₂, ..., x_n} of size n. Instead of the complicated notation using commas between the individual observations, we could write the n observations in terms of vector notation as follows

Equation B.1. 

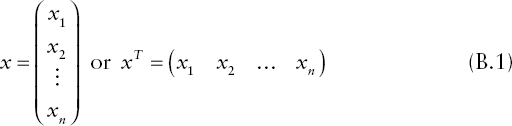
where the left side in equation (B.1) denotes x as a column vector while the right side denotes it as a row vector. Both vectors are of length n (coordinates) since all observations have to be accounted for. Note that the right (row) vector is the transpose of the left (column) vector and vice versa. The transpose is obtained by simply turning the vector by 90 degrees, which is indicated by the upper index T. We could have defined x as a row vector instead and the transpose would then be the column vector. By doing so, we shift the dimensionality of the vectors. The column vector is often indicated by the size n × 1 meaning n rows and 1 column. A row vector is indicated by size 1 × n meaning just one row and n columns.

Suppose there is a second series of observations of the same length n as x, say y = (y₁, y₂, ..., y_n). This second series of observation could be written as a vector. However, x and y could both ...