Probability, Random Variables, and Random Processes: Theory and Signal Processing Applications

C.3 z-TRANSFORM

Definition: z-Transform X(z) The z-transform of x[k] for is

(C.23)

where is a complex variable. The sum converges to X(z) for some ROC on the z-plane as depicted in Figure C.3 for the four basic types of sequences.

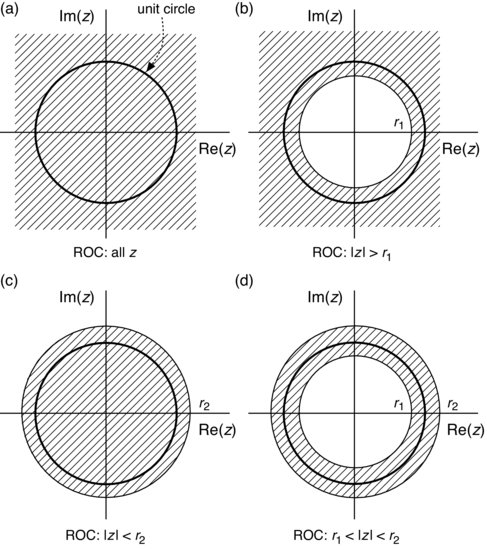
FIGURE C.3 z-plane and ROCs for X(z). The unit circle is defined by |z| = 1. (a) Finite-duration sequence. (b) Right-sided sequence. (c) Left-sided sequence. (d) Two-sided sequence. A sequence is bounded (stable) if the ROC includes the unit circle, which means r1<1 and r2>1. The z-transform does not exist if r1>r2.

The mapping from the s-plane to the z-plane when a continuous-time signal x(t) is uniformly sampled to generate the discrete-time sequence x[k] is described in Chapter 1. For the unilateral Laplace transform, the integral has a finite lower limit, usually zero:

(C.24)

The unilateral and bilateral z-transforms are identical when x[k] is nonzero only for , which can be emphasized by writing x[k]u[k], where u[k] is the discrete unit-step function. ...