Probability, Random Variables, and Random Processes: Theory and Signal Processing Applications

D.1 REVIEW OF RIEMANN INTEGRAL

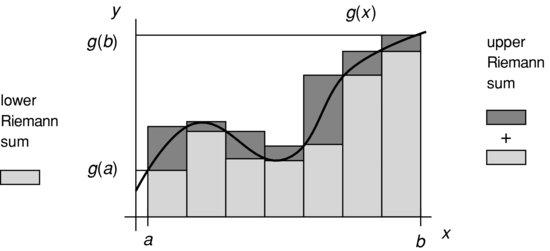
The Riemann integral is covered in introductory calculus courses, and is the integral used in Chapters 3 and 4 on random variables. Consider the function y = g(x) depicted in Figure D.1 which is continuous and bounded on [a, b]. Note that in general an integrable function need not be continuous. Differentiable functions form a subset of continuous functions, and continuous functions form a subset of integrable functions. Later we consider integrals of functions that are not continuous.

FIGURE D.1 Function y = g(x) partitioned on the x-axis into subintervals on [a, b]. Light-shaded rectangles comprise the lower Riemann sum. Light-plus-dark-shaded rectangles comprise the upper Riemann sum.

Example D.1. The rectangle function can be written as rect(x) = u(x + 1/2)−u(x−1/2) where u(x) is the unit-step function. It is clear that rect(x) is not differentiable or continuous at , but is integrable on [−1/2, 1/2]: it has unit area. The triangle function tri(x) = (1−|x|)rect(x/2) is continuous and integrable on [−1, 1], but is not differentiable at x = 0.

Observe in Figure D.1 that [a, b] on the x-axis has been partitioned into a collection of subintervals {[xn, xn + 1]} for . Let be a point in the nth subinterval [xn, xn + 1]. The mesh of the partition is ...