Probability, Random Variables, and Random Processes: Theory and Signal Processing Applications

5.19 ORTHOGONALITY

Orthogonality is a property of two random variables that is useful for applications such as parameter estimation (Chapter 9) and signal estimation (Chapter 11).

Definition: Orthogonal Random variables X and Y are orthogonal if .

This definition follows from a generalized form of orthogonal functions: two deterministic functions g1(x) and g2(x) are orthogonal if

(5.252)

where w(x) is a positive weighting function. In our case, the weighting function is the joint pdf of X and Y, and the integration is performed over two variables:

(5.253)

The connections between independence, uncorrelated, and orthogonal for two random variables are described in the following theorem.

Theorem 5.10 For random variables X and Y:

• Independence implies uncorrelated: (5.254)
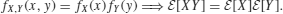
• Uncorrelated and orthogonal are the same when at least one of the random variables has zero mean: (5.255)

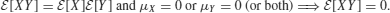
Proof. The proofs follow immediately from the statements.

Although uncorrelated and orthogonal are the same ...