Probability, Random Variables, and Random Processes: Theory and Signal Processing Applications

6.9 MARKOV SEQUENCE

The next property of a random sequence involves conditioning across several time instants.

Definition: Markov Sequence Markov sequence X[k] is a time-indexed set of random variables that satisfies the following Markov property:

(6.79)

A Markov sequence is also called a Markov chain.

For a Markov sequence, the probability of an outcome at a particular time instant given the outcomes at all previous time instants requires conditioning only on the most recent outcome; the complete history of outcomes is not needed. The property in (6.79) is sometimes referred to as one-step Markov; it can be generalized to m steps as follows.

Definition: Order-m Markov Sequence An order-m Markov sequence X[k] has the following property for k>m:

(6.80)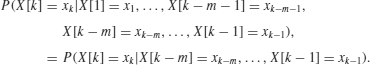

Although a Markov sequence can be described for a countably infinite set of outcomes, most Markov applications involve sequences with a finite number of outcomes. Such random sequences can be represented by a finite number of states.

Definition: States of a Markov Chain The states of a Markov chain are the possible outcomes of the random variable X[k] at any time instant k.

For notational convenience, we represent the one-step conditional probability as follows:

(6.81)

The process is assumed to be stationary such that {pmn} do not ...