Probability, Random Variables, and Random Processes: Theory and Signal Processing Applications

7.4 CENTRAL LIMIT THEOREM

The central limit theorem (CLT) describes an important property of a sum of independent random variables.

Theorem 7.7 (Central limit). Let X[k] be an iid random sequence with mean and variance , and define the following function of the sample mean:

(7.55)

Then has the standard Gaussian distribution.

This theorem refers to a specific convergence in distribution.

Proof. The characteristic function of the sample mean is

(7.56)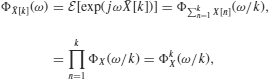

where 1/k scaling has been grouped with ω, and the iid assumption gives the last result. It is straightforward to show that for the transformation in (7.55) (see Problem 7.13):

(7.57)

For notational convenience, define and write the following ...