Probability, Random Variables, and Random Processes: Theory and Signal Processing Applications

8.13 PARAMETRIC MODELS

The parametric approach to spectrum estimation is a type of system identification as illustrated in Figure 8.28. The model assumes that random sequence X[k] is generated as the output of an unknown filter with transfer function H(z), whose input is the white-noise sequence W[k]. The basic types of systems are known as autoregressive (AR), MA, and ARMA models, and are described in the next few sections. For a particular realization X[k], the goal is to estimate the parameters of H(z) such that when the estimated system is driven by white noise, its output closely approximates X[k]. Some issues with this approach include: (i) the type of model, (ii) the order of the model (number of parameters), and (iii) the method of calculating the parameter values. Since the parametric estimate is derived only from the output X[k], the modeling approach is sometimes called “blind” because the input W[k] is not observable. The more general system identification problem assumes that both the input and the output of the model are available; techniques for estimating filter parameters for that case are mentioned briefly at the end of this chapter.

Figure 8.28 System identification framework for parametric spectrum analysis.

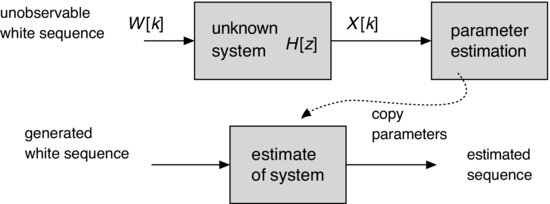
Given the previous model framework, correlation is an important feature of X[k] that is exploited to estimate the model parameters. Since the input is ...